|
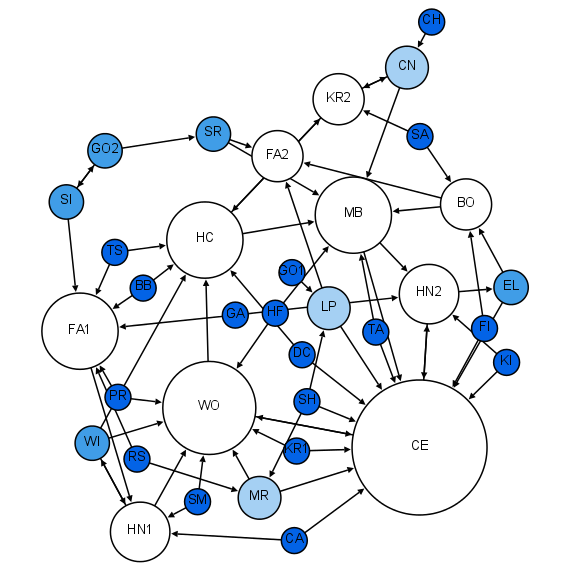
Network Entropy
In network science, the network entropy is a disorder measure derived from information theory to describe the level of randomness and the amount of information encoded in a graph. It is a relevant metric to quantitatively characterize real complex networks and can also be used to quantify network complexity Formulations According to a 2018 publication by Zenil ''et al.'' there are several formulations by which to calculate network entropy and, as a rule, they all require a particular property of the graph to be focused, such as the adjacency matrix, degree sequence, degree distribution or number of bifurcations, what might lead to values of entropy that aren't invariant to the chosen network description. Degree Distribution Shannon Entropy The Shannon entropy can be measured for the network degree probability distribution as an average measurement of the heterogeneity of the network. \mathcal = - \sum_^ P(k) \ln This formulation has limited use with regards to complexity, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Science
Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by ''nodes'' (or ''vertices'') and the connections between the elements or actors as ''links'' (or ''edges''). The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena." Background and history The study of networks has emerged in diverse disciplines as a means of analyzing complex relational data. The earliest known paper in this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SARS-CoV-2
Severe acute respiratory syndrome coronavirus 2 (SARS‑CoV‑2) is a strain of coronavirus that causes COVID-19 (coronavirus disease 2019), the respiratory illness responsible for the ongoing COVID-19 pandemic. The virus previously had a Novel coronavirus, provisional name, 2019 novel coronavirus (2019-nCoV), and has also been called the human coronavirus 2019 (HCoV-19 or hCoV-19). First identified in the city of Wuhan, Hubei, China, the World Health Organization declared the outbreak a public health emergency of international concern on January 30, 2020, and a pandemic on March 11, 2020. SARS‑CoV‑2 is a positive-sense single-stranded RNA virus that is Contagious disease, contagious in humans. SARS‑CoV‑2 is a virus of the species ''severe acute respiratory syndrome–related coronavirus'' (SARSr-CoV), related to the Severe acute respiratory syndrome coronavirus 1, SARS-CoV-1 virus that caused the 2002–2004 SARS outbreak. Despite its close relation to SARS-CoV-1, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Ensemble
In statistical mechanics, a canonical ensemble is the statistical ensemble that represents the possible states of a mechanical system in thermal equilibrium with a heat bath at a fixed temperature. The system can exchange energy with the heat bath, so that the states of the system will differ in total energy. The principal thermodynamic variable of the canonical ensemble, determining the probability distribution of states, is the absolute temperature (symbol: ). The ensemble typically also depends on mechanical variables such as the number of particles in the system (symbol: ) and the system's volume (symbol: ), each of which influence the nature of the system's internal states. An ensemble with these three parameters is sometimes called the ensemble. The canonical ensemble assigns a probability to each distinct microstate given by the following exponential: :P = e^, where is the total energy of the microstate, and is the Boltzmann constant. The number is the free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Limit
In statistical mechanics, the thermodynamic limit or macroscopic limit, of a system is the limit for a large number of particles (e.g., atoms or molecules) where the volume is taken to grow in proportion with the number of particles.S.J. Blundell and K.M. Blundell, "Concepts in Thermal Physics", Oxford University Press (2009) The thermodynamic limit is defined as the limit of a system with a large volume, with the particle density held fixed. : N \to \infty,\, V \to \infty,\, \frac N V =\text In this limit, macroscopic thermodynamics is valid. There, thermal fluctuations in global quantities are negligible, and all thermodynamic quantities, such as pressure and energy, are simply functions of the thermodynamic variables, such as temperature and density. For example, for a large volume of gas, the fluctuations of the total internal energy are negligible and can be ignored, and the average internal energy can be predicted from knowledge of the pressure and temperature of the ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to , 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper "A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (statistical Thermodynamics)
The concept entropy was first developed by German physicist Rudolf Clausius in the mid-nineteenth century as a thermodynamic property that predicts that certain spontaneous processes are irreversible or impossible. In statistical mechanics, entropy is formulated as a statistical property using probability theory. The statistical entropy perspective was introduced in 1870 by Austrian physicist Ludwig Boltzmann, who established a new field of physics that provided the descriptive linkage between the macroscopic observation of nature and the microscopic view based on the rigorous treatment of a large ensembles of microstates that constitute thermodynamic systems. Boltzmann's principle Ludwig Boltzmann defined entropy as a measure of the number of possible microscopic states (''microstates'') of a system in thermodynamic equilibrium, consistent with its macroscopic thermodynamic properties, which constitute the ''macrostate'' of the system. A useful illustration is the example of a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency Matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is undirected (i.e. all of its edges are bidirectional), the adjacency matrix is symmetric. The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory. The adjacency matrix of a graph should be distinguished from its incidence matrix, a different matrix representation whose elements indicate whether vertex–edge pairs are incident or not, and its degree matrix, which contains information about the degree of each vertex. Definition For a simple graph with vertex set , the adjacency matrix is a square matrix such that its element is one when there is an edge from vertex to vert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Ensemble
In statistical mechanics, a canonical ensemble is the statistical ensemble that represents the possible states of a mechanical system in thermal equilibrium with a heat bath at a fixed temperature. The system can exchange energy with the heat bath, so that the states of the system will differ in total energy. The principal thermodynamic variable of the canonical ensemble, determining the probability distribution of states, is the absolute temperature (symbol: ). The ensemble typically also depends on mechanical variables such as the number of particles in the system (symbol: ) and the system's volume (symbol: ), each of which influence the nature of the system's internal states. An ensemble with these three parameters is sometimes called the ensemble. The canonical ensemble assigns a probability to each distinct microstate given by the following exponential: :P = e^, where is the total energy of the microstate, and is the Boltzmann constant. The number is the free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Microcanonical Ensemble
In statistical mechanics, the microcanonical ensemble is a statistical ensemble that represents the possible states of a mechanical system whose total energy is exactly specified. The system is assumed to be isolated in the sense that it cannot exchange energy or particles with its environment, so that (by conservation of energy) the energy of the system does not change with time. The primary macroscopic variables of the microcanonical ensemble are the total number of particles in the system (symbol: ), the system's volume (symbol: ), as well as the total energy in the system (symbol: ). Each of these is assumed to be constant in the ensemble. For this reason, the microcanonical ensemble is sometimes called the ensemble. In simple terms, the microcanonical ensemble is defined by assigning an equal probability to every microstate whose energy falls within a range centered at . All other microstates are given a probability of zero. Since the probabilities must add up to 1, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. This established the fields of statistical thermodynamics and statistical physics. The founding of the field of statistical mechanics is generally credited to three physicists: *Ludwig Boltzmann, who developed the fundamental interpretation of entropy in terms of a collection of microstates *James Clerk Maxwell, who developed models of probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Network
A Boolean network consists of a discrete set of boolean variables each of which has a Boolean function (possibly different for each variable) assigned to it which takes inputs from a subset of those variables and output that determines the state of the variable it is assigned to. This set of functions in effect determines a topology (connectivity) on the set of variables, which then become nodes in a network. Usually, the dynamics of the system is taken as a discrete time series where the state of the entire network at time ''t''+1 is determined by evaluating each variable's function on the state of the network at time ''t''. This may be done synchronously or asynchronously. Boolean networks have been used in biology to model regulatory networks. Although Boolean networks are a crude simplification of genetic reality where genes are not simple binary switches, there are several cases where they correctly convey the correct pattern of expressed and suppressed genes. The se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ginestra Bianconi
Ginestra Bianconi is a network scientist and mathematical physicist, known for her work on statistical mechanics, network theory, multilayer and higher-order networks, and in particular for the Bianconi–Barabási model of growing of complex networks and for the Bose–Einstein condensation (network theory) in complex networks. She is a professor of applied mathematics at Queen Mary University of London, and the editor-in-chief of '' Journal of Physics: Complexity''. Education and career Bianconi earned a laurea in physics from Sapienza University of Rome in 1998, advised by Luciano Pietronero, and a PhD from the University of Notre Dame in 2002, advised by Albert-László Barabási. After postdoctoral research at the University of Fribourg in Switzerland and the International Centre for Theoretical Physics in Italy, she became an assistant professor at Northeastern University in 2009. She moved to Queen Mary University of London in 2013, and became professor there in 201 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |