|
Neighborhood Semantics
Neighborhood semantics, also known as Scott–Montague semantics, is a formal semantics for modal logics. It is a generalization, developed independently by Dana Scott and Richard Montague, of the more widely known relational semantics for modal logic. Whereas a relational frame \langle W,R\rangle consists of a set ''W'' of worlds (or states) and an accessibility relation ''R'' intended to indicate which worlds are alternatives to (or, accessible from) others, a neighborhood frame \langle W,N\rangle still has a set ''W'' of worlds, but has instead of an accessibility relation a ''neighborhood function'' : N : W \to 2^ that assigns to each element of ''W'' a set of subsets of ''W''. Intuitively, each family of subsets assigned to a world are the propositions necessary at that world, where 'proposition' is defined as a subset of ''W'' (i.e. the set of worlds at which the proposition is true). Specifically, if ''M'' is a model on the frame, then : M,w\models\square \varphi \L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Logic
Modal logic is a kind of logic used to represent statements about Modality (natural language), necessity and possibility. In philosophy and related fields it is used as a tool for understanding concepts such as knowledge, obligation, and causality, causation. For instance, in epistemic modal logic, the well-formed_formula, formula \Box P can be used to represent the statement that P is known. In deontic modal logic, that same formula can represent that P is a moral obligation. Modal logic considers the inferences that modal statements give rise to. For instance, most epistemic modal logics treat the formula \Box P \rightarrow P as a Tautology_(logic), tautology, representing the principle that only true statements can count as knowledge. However, this formula is not a tautology in deontic modal logic, since what ought to be true can be false. Modal logics are formal systems that include unary operation, unary operators such as \Diamond and \Box, representing possibility and necessi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dana Scott
Dana Stewart Scott (born October 11, 1932) is an American logician who is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California. His work on automata theory earned him the Turing Award in 1976, while his collaborative work with Christopher Strachey in the 1970s laid the foundations of modern approaches to the semantics of programming languages. He has also worked on modal logic, topology, and category theory. Early career He received his B.A. in Mathematics from the University of California, Berkeley, in 1954. He wrote his Ph.D. thesis on ''Convergent Sequences of Complete Theories'' under the supervision of Alonzo Church while at Princeton, and defended his thesis in 1958. Solomon Feferman (2005) writes of this period: After completing his Ph.D. studies, he moved to the University of Chicago, working as an instructor there until 1960. In 1959, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard Montague
Richard Merritt Montague (September 20, 1930 – March 7, 1971) was an American mathematician and philosopher who made contributions to mathematical logic and the philosophy of language. He is known for proposing Montague grammar to formalize the semantics of natural language. As a student of Alfred Tarski, he also contributed early developments to axiomatic set theory ( ZFC). For the latter half of his life, he was a professor at the University of California, Los Angeles until his early death, believed to be a homicide, at age 40. Career At the University of California, Berkeley, Montague earned a BA in philosophy in 1950, an MA in mathematics in 1953, and a PhD in Philosophy in 1957, the latter under the direction of the mathematician and logician Alfred Tarski. Montague spent his entire career teaching in the UCLA Department of Philosophy, where he supervised the dissertations of Nino Cocchiarella and Hans Kamp. Montague wrote on the foundations of logic and set theory, as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kripke Semantics
Kripke semantics (also known as relational semantics or frame semantics, and often confused with possible world semantics) is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke (algebraic semantics existed, but were considered 'syntax in disguise'). Semantics of modal logic The language of propositional modal logic consists of a countably infinite set of propositional variables, a set of truth-functional connectives (in this article \to and \neg), and the modal operator \Box ("necessarily"). The modal operator \Diamond ("possibly") is (classically) the dual of \Box and may be defined in terms of necessity like so: \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
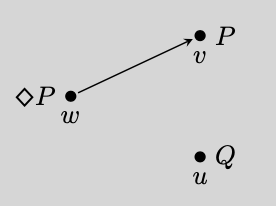
Accessibility Relation
An accessibility relation is a relation (math), relation which plays a key role in assigning truth values to sentences in the Kripke semantics, relational semantics for modal logic. In relational semantics, a modal formula's truth value at a ''possible world'' w can depend on what is true at another possible world v, but only if the accessibility relation R relates w to v. For instance, if P holds at some world v such that wRv, the formula \Diamond P will be true at w. The fact wRv is crucial. If R did not relate w to v, then \Diamond P would be false at w unless P also held at some other world u such that wRu. Accessibility relations are motivated conceptually by the fact that natural language linguistic modality, modal statements depend on some, but not all, alternative scenarios. For instance, the sentence "It might be raining" is not generally judged true simply because one can imagine a scenario where it is raining. Rather, its truth depends on whether such a scenario is r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Modal Logic
In modal logic, a classical modal logic L is any modal logic containing (as axiom or theorem) the duality of the modal operators :\Diamond A \leftrightarrow \lnot\Box\lnot A that is also closed under the rule :\frac. Alternatively, one can give a dual definition of L by which L is classical if and only if it contains (as axiom or theorem) :\Box A \leftrightarrow \lnot\Diamond\lnot A and is closed under the rule :\frac. The weakest classical system is sometimes referred to as E and is non-normal. Both algebraic and neighborhood semantics characterize familiar classical modal systems that are weaker than the weakest normal modal logic K. Every regular modal logic is classical, and every normal modal logic In logic, a normal modal logic is a set ''L'' of modal formulas such that ''L'' contains: * All propositional tautology (logic), tautologies; * All instances of the Kripke_semantics, Kripke schema: \Box(A\to B)\to(\Box A\to\Box B) and it is closed ... is regular and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Modal Logic
In logic, a normal modal logic is a set ''L'' of modal formulas such that ''L'' contains: * All propositional tautology (logic), tautologies; * All instances of the Kripke_semantics, Kripke schema: \Box(A\to B)\to(\Box A\to\Box B) and it is closed under: * Detachment rule (''modus ponens''): A\to B, A \in L implies B \in L; * Necessitation rule: A \in L implies \Box A \in L. The smallest logic satisfying the above conditions is called K. Most modal logics commonly used nowadays (in terms of having philosophical motivations), e.g. C. I. Lewis's S4 and S5 (modal logic), S5, are normal (and hence are extensions of K). However a number of deontic logic, deontic and epistemic logics, for example, are non-normal, often because they give up the Kripke schema. Every normal modal logic is regular modal logic, regular and hence classical modal logic, classical. Common normal modal logics The following table lists several common normal modal systems. The notation refers to the table at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Frame
In logic, general frames (or simply frames) are Kripke frames with an additional structure, which are used to model modal logic, modal and intermediate logic, intermediate logics. The general frame semantics combines the main virtues of Kripke semantics and algebraic semantics (mathematical logic), algebraic semantics: it shares the transparent geometrical insight of the former, and robust completeness of the latter. Definition A modal general frame is a triple \mathbf F=\langle F,R,V\rangle, where \langle F,R\rangle is a Kripke frame (i.e., R is a binary relation on the set F), and V is a set of subsets of F that is closed under the following: *the Boolean operations of (binary) intersection (set theory), intersection, union (set theory), union, and complement (set theory), complement, *the operation \Box, defined by \Box A=\. They are thus a special case of field of sets#Fields of sets with additional structure, fields of sets with additional structure. The purpose of V is to rest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoria (philosophy Journal)
''Theoria: A Swedish Journal of Philosophy and Psychology'' is a peer-reviewed academic journal publishing research in all areas of philosophy established in 1935 by Åke Petzäll ( sv). It is published quarterly by Wiley-Blackwell on behalf of Stiftelsen Theoria. The current editor-in-chief is Sven Ove Hansson. ''Theoria'' publishes articles, reviews, and shorter notes and discussions. Editors Notable articles Among the contributions to philosophy, logic, and mathematics first published in ''Theoria'' are: * Carl Gustav Hempel, Le problème de la vérité, ''Theoria'' 3, 1937, 206–244. ( Hempel's confirmation paradoxes) * Ernst Cassirer, Was ist "Subjektivismus"?, ''Theoria'' 5, 1939, 111–140. * Alf Ross, Imperatives and Logic, ''Theoria'' 7, 1941, 53–71. ( Ross' deontic paradox) * Georg Henrik von Wright, The Paradoxes of Confirmation, ''Theoria'' 31, 1965, 255–274. * Per Lindström, First Order Predicate Logic with Generalized Quantifiers, ''Theoria'' 32, 1966, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |