|
Missing Square Puzzle
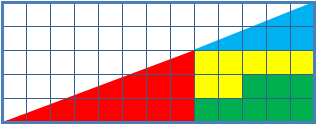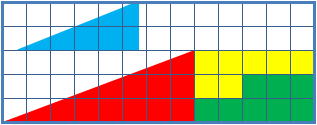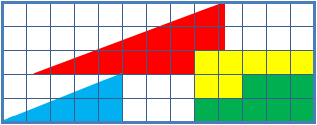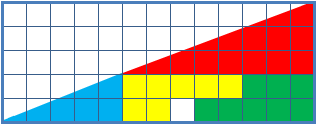
The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures; or rather to teach them not to reason using figures, but to use only textual descriptions and the axioms of geometry. It depicts two arrangements made of similar shapes in slightly different configurations. Each apparently forms a 13×5 right-angled triangle, but one has a 1×1 hole in it. Solution The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, nor would either truly be 13x5 if it were, because what appears to be the hypotenuse is bent. In other words, the "hypotenuse" does not maintain a consistent slope, even though it may appear that way to the human eye. A true 13×5 triangle cannot be created from the given component parts. The four figures (the yellow, red, blue and green shapes) total 32 units of area. The apparent triangles formed from the figures are 13 units wide and 5 units tall, so it appears ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Missing Square Animation
Missing or The Missing may refer to: Film * ''Missing'' (1918 film), an American silent drama directed by James Young * ''Missing'' (1982 film), an American historical drama directed by Costa-Gavras about the 1973 coup in Chile *, a Belgian film that was a 2007 box office number-one film in Belgium *''Missing'', a 2007 film featuring Nao Ōmori * ''Missing'' (2008 film), a Hong Kong horror film directed by Tsui Hark *, a South Korean film directed by Kim Sung-hong * ''Missing'' (2009 short film), a film starring Susan Glover * ''Missing'' (2010 film), a Jordanian film directed by Tariq Rimawi * ''Missing'' (2016 film), a South Korean film directed by Lee Eon-hee * ''Missing'' (2018 film), an Indian film directed by Mukul Abhyankar * ''Missing'' (2019 film), a Hong Kong film directed by Ronnie Chau * ''Missing'' (2023 film), an American thriller film *''Missing'', a 2024 film featuring Satomi Ishihara * ''The Missing'' (1999 film), an Australian film directed by Manuela Alberti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissection Puzzle
A dissection puzzle, also called a transformation puzzle or Richter puzzle, is a tiling puzzle where a set of pieces can be assembled in different ways to produce two or more distinct geometric shapes. The creation of new dissection puzzles is also considered to be a type of dissection puzzle. Puzzles may include various restraints, such as hinged pieces, pieces that can fold, or pieces that can twist. Creators of new dissection puzzles emphasize using a minimum number of pieces, or creating novel situations, such as ensuring that every piece connects to another with a hinge. History Dissection puzzles are an early form of geometric puzzle. The earliest known descriptions of dissection puzzles are from the time of Plato (427–347 BCE) in Ancient Greece, and involve the challenge of turning two equal squares into one larger square using four pieces. Other ancient dissection puzzles were used as graphic depictions of the Pythagorean theorem (see square trisection). A fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Paradoxes
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of abstract objects that consist of either abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to prove properties of objects, a ''proof'' consisting of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Mathematics
Elementary mathematics, also known as primary or secondary school mathematics, is the study of mathematics topics that are commonly taught at the primary or secondary school levels around the world. It includes a wide range of mathematical concepts and skills, including number sense, algebra, geometry, measurement, and data analysis. These concepts and skills form the foundation for more advanced mathematical study and are essential for success in many fields and everyday life. The study of elementary mathematics is a crucial part of a student's education and lays the foundation for future academic and career success. Strands of elementary mathematics Number sense and numeration Number sense is an understanding of numbers and operations. In the 'Number Sense and Numeration' strand students develop an understanding of numbers by being taught various ways of representing numbers, as well as the relationships among numbers. Properties of the natural numbers such as divisibil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Illusions
In visual perception, an optical illusion (also called a visual illusion) is an illusion caused by the visual system and characterized by a visual percept that arguably appears to differ from reality. Illusions come in a wide variety; their categorization is difficult because the underlying cause is often not clear but a classification proposed by Richard Gregory is useful as an orientation. According to that, there are three main classes: physical, physiological, and cognitive illusions, and in each class there are four kinds: Ambiguities, distortions, paradoxes, and fictions. A classical example for a physical distortion would be the apparent bending of a stick half immersed in water; an example for a physiological paradox is the motion aftereffect (where, despite movement, position remains unchanged). An example for a physiological fiction is an afterimage. Three typical cognitive distortions are the Ponzo, Poggendorff, and Müller-Lyer illusion. Physical illusions are cau ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chocolate Bar
A chocolate bar is a confection containing chocolate, which may also contain layerings or mixtures that include nut (fruit), nuts, fruit, caramel, nougat, and wafers. A flat, easily breakable, chocolate bar is also called a tablet. In some varieties of English and food labeling standards, the term ''chocolate bar'' is reserved for bars of solid chocolate, with ''candy bar'' used for products with additional ingredients. The manufacture of a chocolate bar from raw cocoa bean, cocoa ingredients requires many steps, from grinding and refining, to conching and tempering. All these processes have been independently developed by chocolate manufacturers from different countries. There is therefore no precise moment when the first chocolate bar came into existence. Solid chocolate was already consumed in the 18th century. The 19th century saw the emergence of the modern chocolate industry; most manufacturing techniques used today were invented during this period. Dark chocolate, Dark, mi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet Union, Soviet-born Israeli Americans, Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow Institute of Electronics and Mathematics, senior instructor at Hebrew University and software consultant at Ben Gurion University. He wrote extensively about arithmetic, probability, algebra, geometry, trigonometry and mathematical games. He was known for his contribution to heuristics and mathematics education, creating and maintaining the mathematically themed educational website ''Cut-the-Knot'' for the Mathematical Association of America (MAA) Online. He was a pioneer in mathematical education on the internet, having started ''Cut-the-Knot'' in October 1996. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vanishing Puzzle
A vanishing puzzle is a mechanical puzzle, mechanical optical illusion comprising multiple pieces which can be rearranged to show different versions of a picture depicting several objects, the number of which depending on the arrangement of the pieces. History Wemple & Company marketed an advertising card named ''The Magic Egg Puzzle, (How Many Eggs?)'' in New York in 1880. Cutting the rectangular card into four oblongs allowed the pieces to be rearranged to show either 8, 9 or 10 eggs. Many other similar puzzles have been published since. Chess player and recreational mathematician Sam Loyd patented rotary vanishing puzzles in 1896 and published versions named ''Get Off the Earth'', ''Teddy and the Lion'' and ''The Disappearing Bicyclist'' (pictured). Each had a circular card connected to a cardboard backdrop with a pin, letting it freely rotate. In ''The Disappearing Bicyclist'', when the disc is rotated such that the arrow points to A, 13 boys can be counted, but when i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Disappearing Bicyclist Vanishing Puzzle
''The'' is a grammatical article in English, denoting nouns that are already or about to be mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with nouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of the archaic pronoun ''thee' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secant (trigonometry)
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple polygon, simple (not self-intersecting), or complex polygon, complex (self-intersecting, or crossed). Simple quadrilaterals are either convex polygon, convex or concave polygon, concave. The Internal and external angle, interior angles of a simple (and Plane (geometry), planar) quadrilateral ''ABCD'' add up to 360 Degree (angle), degrees, that is :\angle A+\angle B+\angle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chessboard Paradox
The chessboard paradoxGreg N. Frederickson: ''Dissections: Plane and Fancy''. Cambridge University Press, 2003, , chapter 23, pp. 268–277 in particular pp. 271–274 Colin Foster: "Slippery Slopes". In: ''Mathematics in School'', vol. 34, no. 3 (May, 2005), pp. 33–34JSTOR or paradox of Loyd and SchlömilchFranz Lemmermeyer: ''Mathematik à la Carte: Elementargeometrie an Quadratwurzeln mit einigen geschichtlichen Bemerkungen''. Springer 2014, , pp95–96(German) is a falsidical paradox based on an optical illusion. A chessboard or a square with a side length of 8 units is cut into four pieces. Those four pieces are used to form a rectangle with side lengths of 13 and 5 units. Hence the combined area of all four pieces is 64 area units in the square but 65 area units in the rectangle, this seeming contradiction is due an optical illusion as the four pieces don't fit exactly in the rectangle, but leave a small barely visible gap around the rectangle's diagonal. The paradox is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |