|
Meta-regression
Meta-regression is defined to be a meta-analysis that uses regression analysis to combine, compare, and synthesize research findings from multiple studies while adjusting for the effects of available covariates on a response variable. A meta-regression analysis aims to reconcile conflicting studies or corroborate consistent ones; a meta-regression analysis is therefore characterized by the collated studies and their corresponding data sets—whether the response variable is study-level (or equivalently ''aggregate'') data or individual participant data (or individual patient data in medicine). A data set is ''aggregate'' when it consists of summary statistics such as the sample mean, effect size, or odds ratio. On the other hand, individual participant data are in a sense ''raw'' in that all observations are reported with no abridgment and therefore no information loss. Aggregate data are easily compiled through internet search engines and therefore not expensive. However, indi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meta-analysis
A meta-analysis is a statistical analysis that combines the results of multiple scientific studies. Meta-analyses can be performed when there are multiple scientific studies addressing the same question, with each individual study reporting measurements that are expected to have some degree of error. The aim then is to use approaches from statistics to derive a pooled estimate closest to the unknown common truth based on how this error is perceived. Meta-analytic results are considered the most trustworthy source of evidence by the evidence-based medicine literature.Herrera Ortiz AF., Cadavid Camacho E, Cubillos Rojas J, Cadavid Camacho T, Zoe Guevara S, Tatiana Rincón Cuenca N, Vásquez Perdomo A, Del Castillo Herazo V, & Giraldo Malo R. A Practical Guide to Perform a Systematic Literature Review and Meta-analysis. Principles and Practice of Clinical Research. 2022;7(4):47–57. https://doi.org/10.21801/ppcrj.2021.74.6 Not only can meta-analyses provide an estimate of the u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (that is, the variables tend to show opposite behavior), the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation. A distinction must be made between (1) the covariance of two ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the '' average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results of an experiment or an observational study, or frequently a set of results from a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics, because it helps distinguish it from other means, such as the geometric mean and the harmonic mean. In addition to mathematics and statistics, the arithmetic mean is used frequently in many diverse fields such as economics, anthropology and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effect Size
In statistics, an effect size is a value measuring the strength of the relationship between two variables in a population, or a sample-based estimate of that quantity. It can refer to the value of a statistic calculated from a sample of data, the value of a parameter for a hypothetical population, or to the equation that operationalizes how statistics or parameters lead to the effect size value. Examples of effect sizes include the correlation between two variables, the regression coefficient in a regression, the mean difference, or the risk of a particular event (such as a heart attack) happening. Effect sizes complement statistical hypothesis testing, and play an important role in power analyses, sample size planning, and in meta-analyses. The cluster of data-analysis methods concerning effect sizes is referred to as estimation statistics. Effect size is an essential component when evaluating the strength of a statistical claim, and it is the first item (magnitude) in the MA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odds Ratio
An odds ratio (OR) is a statistic that quantifies the strength of the association between two events, A and B. The odds ratio is defined as the ratio of the odds of A in the presence of B and the odds of A in the absence of B, or equivalently (due to symmetry), the ratio of the odds of B in the presence of A and the odds of B in the absence of A. Two events are independent if and only if the OR equals 1, i.e., the odds of one event are the same in either the presence or absence of the other event. If the OR is greater than 1, then A and B are associated (correlated) in the sense that, compared to the absence of B, the presence of B raises the odds of A, and symmetrically the presence of A raises the odds of B. Conversely, if the OR is less than 1, then A and B are negatively correlated, and the presence of one event reduces the odds of the other event. Note that the odds ratio is symmetric in the two events, and there is no causal direction implied ( correlation does not imply c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
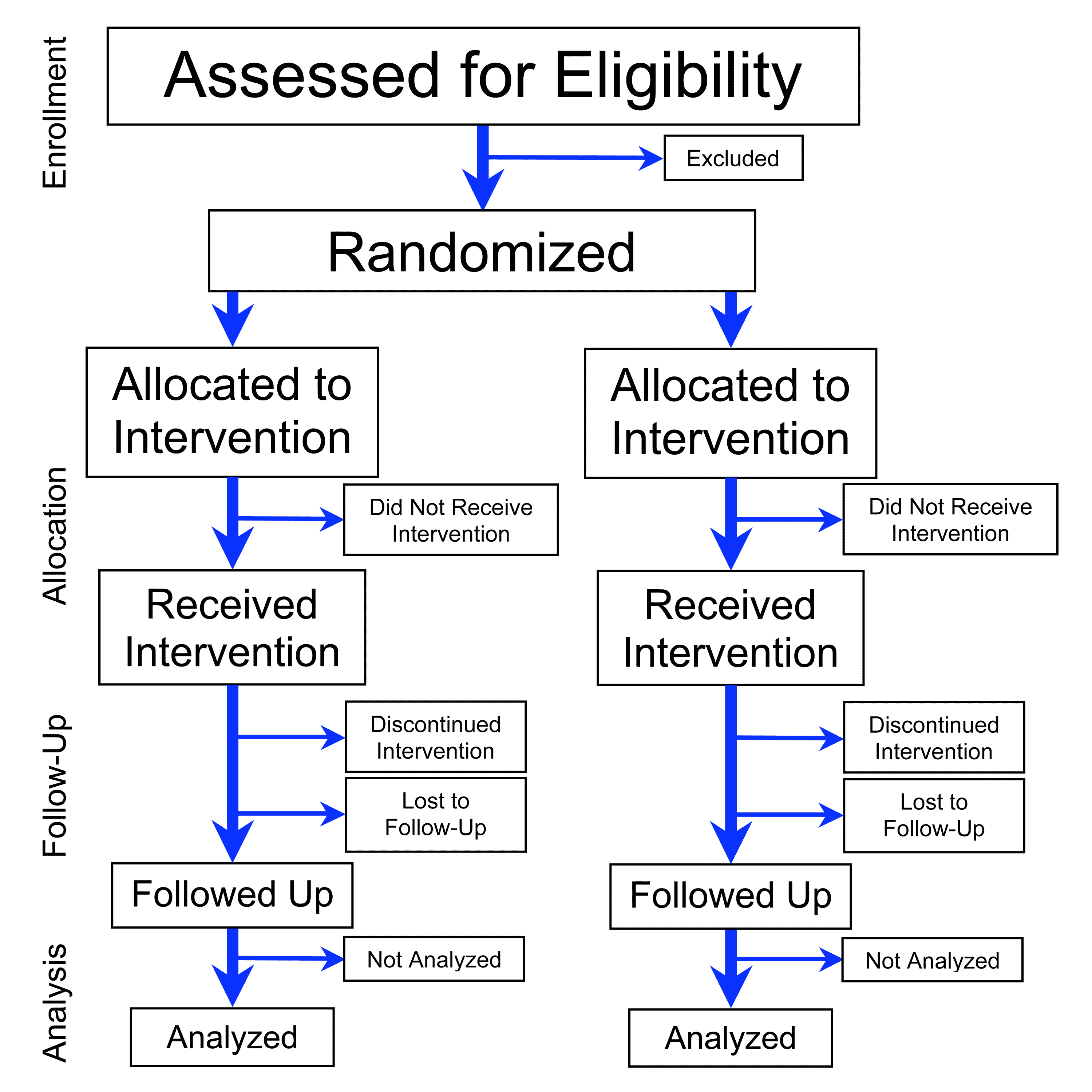
Randomized Controlled Trial
A randomized controlled trial (or randomized control trial; RCT) is a form of scientific experiment used to control factors not under direct experimental control. Examples of RCTs are clinical trials that compare the effects of drugs, surgical techniques, medical devices, diagnostic procedures or other medical treatments. Participants who enroll in RCTs differ from one another in known and unknown ways that can influence study outcomes, and yet cannot be directly controlled. By randomly allocating participants among compared treatments, an RCT enables ''statistical control'' over these influences. Provided it is designed well, conducted properly, and enrolls enough participants, an RCT may achieve sufficient control over these confounding factors to deliver a useful comparison of the treatments studied. Definition and examples An RCT in clinical research typically compares a proposed new treatment against an existing standard of care; these are then termed the 'experime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Therapy
A therapy or medical treatment (often abbreviated tx, Tx, or Tx) is the attempted remediation of a health problem, usually following a medical diagnosis. As a rule, each therapy has indications and contraindications. There are many different types of therapy. Not all therapies are effective. Many therapies can produce unwanted adverse effects. ''Medical treatment'' and ''therapy'' are generally considered synonyms. However, in the context of mental health, the term ''therapy'' may refer specifically to psychotherapy. History Before the creating of therapy as a formal procedure, people told stories to one another to inform and assist about the world. The term "healing through words" was used over 3,500 years ago in Greek and Egyptian writing. The term psychotherapy was invented in the 19th century, and psychoanalysis was founded by Sigmund Freud under a decade later. Semantic field The words ''care'', ''therapy'', ''treatment'', and ''intervention'' overlap in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hierarchy Of Evidence
A hierarchy of evidence (or levels of evidence) is a heuristic used to rank the relative strength of results obtained from scientific research. There is broad agreement on the relative strength of large-scale, epidemiological studies. More than 80 different hierarchies have been proposed for assessing medical evidence. The design of the study (such as a case report for an individual patient or a blinded randomized controlled trial) and the endpoints measured (such as survival or quality of life) affect the strength of the evidence. In clinical research, the best evidence for treatment efficacy is mainly from meta-analyses of randomized controlled trials (RCTs). Systematic reviews of completed, high-quality randomized controlled trials – such as those published by the Cochrane Collaboration – rank the same as systematic review of completed high-quality observational studies in regard to the study of side effects. Evidence hierarchies are often applied in evidence-based pra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
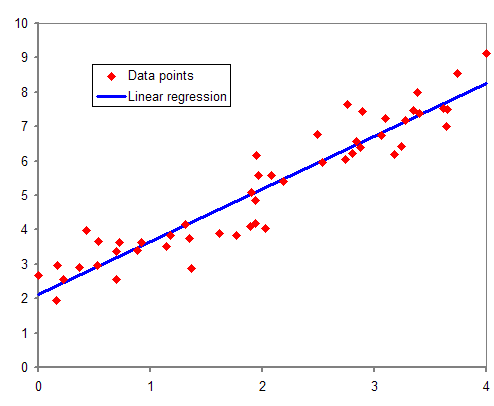
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance-stabilizing Transformation
In applied statistics, a variance-stabilizing transformation is a data transformation that is specifically chosen either to simplify considerations in graphical exploratory data analysis or to allow the application of simple regression-based or analysis of variance techniques. Overview The aim behind the choice of a variance-stabilizing transformation is to find a simple function ''ƒ'' to apply to values ''x'' in a data set to create new values such that the variability of the values ''y'' is not related to their mean value. For example, suppose that the values x are realizations from different Poisson distributions: i.e. the distributions each have different mean values ''μ''. Then, because for the Poisson distribution the variance is identical to the mean, the variance varies with the mean. However, if the simple variance-stabilizing transformation :y=\sqrt \, is applied, the sampling variance associated with observation will be nearly constant: see Anscombe transform fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fisher Transformation
In statistics, the Fisher transformation (or Fisher ''z''-transformation) of a Pearson correlation coefficient is its inverse hyperbolic tangent (artanh). When the sample correlation coefficient ''r'' is near 1 or -1, its distribution is highly skewed, which makes it difficult to estimate confidence intervals and apply tests of significance for the population correlation coefficient ρ. The Fisher transformation solves this problem by yielding a variable whose distribution is approximately normally distributed, with a variance that is stable over different values of ''r''. Definition Given a set of ''N'' bivariate sample pairs (''X''''i'', ''Y''''i''), ''i'' = 1, …, ''N'', the sample correlation coefficient ''r'' is given by :r = \frac = \frac. Here \operatorname(X,Y) stands for the covariance between the variables X and Y and \sigma stands for the standard deviation of the respective variable. Fisher's z-transformation of ''r'' is defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |