|
Mechanical Amplifier
A mechanical amplifier or a mechanical amplifying element is a linkage mechanism that amplifies the magnitude of mechanical quantities such as force, displacement, velocity, acceleration and torque in linear and rotational systems.B.C. Nakra and K.K. Chaudhry, (1985), Instrumentation, Measurement and Analysis, Tata McGraw-Hill Publishing, , page 153. In some applications, mechanical amplification induced by nature or unintentional oversights in man-made designs can be disastrous, causing situations such as the 1940 Tacoma Narrows Bridge collapse. When employed appropriately, it can help to magnify small mechanical signals for practical applications. No additional energy can be created from any given mechanical amplifier due to conservation of energy. Claims of using mechanical amplifiers for perpetual motion machines are false, due to either a lack of understanding of the working mechanism or a simple hoax. Generic mechanical amplifiers Amplifiers, in the most general sense, are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
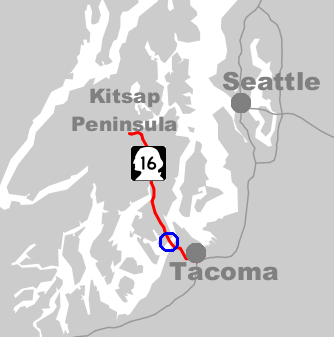
Tacoma Narrows Bridge (1940)
The 1940 Tacoma Narrows Bridge, the first bridge at this location, was a suspension bridge in the U.S. state of Washington that spanned the Tacoma Narrows strait of Puget Sound between Tacoma and the Kitsap Peninsula. It opened to traffic on July 1, 1940, and dramatically collapsed into Puget Sound on November 7 of the same year. The bridge's collapse has been described as "spectacular" and in subsequent decades "has attracted the attention of engineers, physicists, and mathematicians". Throughout its short existence, it was the world's third-longest suspension bridge by main span, behind the Golden Gate Bridge and the George Washington Bridge. Construction began in September 1938. From the time the deck was built, it began to move vertically in windy conditions, so construction workers nicknamed the bridge "Galloping Gertie". The motion continued after the bridge opened to the public, despite several damping measures. The bridge's main span finally collapsed in wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass-Spring-Damper
The mass-spring-damper model consists of discrete mass nodes distributed throughout an object and interconnected via a network of springs and dampers. This form of model is also well-suited for modelling objects with complex material behavior such as those with nonlinearity or viscoelasticity. As well as engineering simulation, these systems have applications in computer graphics and computer animation. Derivation (Single Mass) Deriving the equations of motion for this model is usually done by summing the forces on the mass (including any applied external forces F_\text): :\Sigma F = -kx - c \dot x +F_\text = m \ddot x By rearranging this equation, we can derive the standard form: :\ddot x + 2 \zeta \omega_n \dot x + \omega_n^2 x = u where \omega_n=\sqrt\frac; \quad \zeta = \frac; \quad u=\frac \omega_n is the undamped natural frequency and \zeta is the damping ratio. The homogeneous equation for the mass spring system is: :\ddot x + 2 \zeta \omega_n \dot x + \omega ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transient State
In systems theory, a system is said to be transient or in a transient state when a process variable or variables have been changed and the system has not yet reached a steady state. In electrical engineering, the time taken for an electronic circuit to change from one steady state to another steady state is called the transient time. Examples Chemical Engineering When a chemical reactor is being brought into operation, the concentrations, temperatures, species compositions, and reaction rates are changing with time until operation reaches its nominal process variables. Electrical engineering When a switch is closed in an electrical circuit containing a capacitor or inductor, the component draws out the resulting change in voltage or current, causing the system to take a substantial amount of time to reach a new steady state. This period of time is known as the transient state. A capacitor acts as a short circuit immediately after the switch is closed, increasing its impedanc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Little Girl On Swing
Little is a synonym for small size and may refer to: Arts and entertainment * ''Little'' (album), 1990 debut album of Vic Chesnutt * ''Little'' (film), 2019 American comedy film *The Littles, a series of children's novels by American author John Peterson ** ''The Littles'' (TV series), an American animated series based on the novels Places *Little, Kentucky, United States *Little, West Virginia, United States Other uses *Clan Little, a Scottish clan *Little (surname), an English surname *Little (automobile), an American automobile manufactured from 1912 to 1915 *Little, Brown and Company, an American publishing company * USS ''Little'', multiple United States Navy ships See also * * *Little Mountain (other) *Little River (other) *Little Island (other) Little Island can refer to: Geographical areas Australia * Little Island (South Australia) * Little Island (Tasmania) * Little Island (Western Australia) Canada * Little Island (Lake Kagawong), Ontario ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathieu Function
In mathematics, Mathieu functions, sometimes called angular Mathieu functions, are solutions of Mathieu's differential equation : \frac + (a - 2q\cos(2x))y = 0, where are real-valued parameters. Since we may add to to change the sign of , it is a usual convention to set . They were first introduced by Émile Léonard Mathieu, who encountered them while studying vibrating elliptical drumheads.Morse and Feshbach (1953).Brimacombe, Corless and Zamir (2021) They have applications in many fields of the physical sciences, such as optics, quantum mechanics, and general relativity. They tend to occur in problems involving periodic motion, or in the analysis of partial differential equation (PDE) boundary value problems possessing elliptic symmetry.Gutiérrez-Vega (2015). Definition Mathieu functions In some usages, ''Mathieu function'' refers to solutions of the Mathieu differential equation for arbitrary values of a and q. When no confusion can arise, other authors use the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic
In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the ''fundamental frequency'' of a periodic signal. The fundamental frequency is also called the ''1st harmonic''; the other harmonics are known as ''higher harmonics''. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a '' harmonic series''. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz. In music, harmonics are used on string instruments and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Value Problem
In the study of differential equations, a boundary-value problem is a differential equation subjected to constraints called boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems, in the linear case, involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential equations is devot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Mode
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies. These fixed frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge, or molecule, has a set of normal modes and their natural frequencies that depend on its structure, materials and boundary conditions. The most general motion of a linear system is a superposition of its normal modes. The modes are normal in the sense that they can move independently, that is to say that an excitation of one mode will never cause motion of a different mode. In mathematical terms, normal modes are orthogonal to each other. General definitions Mode In the wave theory of physics and engineering, a mode in a dynamical system is a standing wave st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Q Factor
In physics and engineering, the quality factor or factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in one radian of the cycle of oscillation. factor is alternatively defined as the ratio of a resonator's centre frequency to its bandwidth when subject to an oscillating driving force. These two definitions give numerically similar, but not identical, results. Higher indicates a lower rate of energy loss and the oscillations die out more slowly. A pendulum suspended from a high-quality bearing, oscillating in air, has a high , while a pendulum immersed in oil has a low one. Resonators with high quality factors have low damping, so that they ring or vibrate longer. Explanation The factor is a parameter that describes the resonance behavior of an underdamped harmonic oscillator (resonator). Sinusoidally driven resonators having high ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Damping
In physical systems, damping is the loss of energy of an oscillating system by dissipation. Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. Examples of damping include viscous damping in a fluid (see viscous drag), surface friction, radiation, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes (ex. Suspension (mechanics)). Damping is not to be confused with friction, which is a type of dissipative force acting on a system. Friction can cause or be a factor of damping. Many systems exhibit oscillatory behavior when they are disturbed from their position of static equilibrium. A mass suspended from a spring, for example, might, if pulled and released, bounce up and down. On each bounce, the system tends to return to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Frequency
The fundamental frequency, often referred to simply as the ''fundamental'' (abbreviated as 0 or 1 ), is defined as the lowest frequency of a Periodic signal, periodic waveform. In music, the fundamental is the musical pitch (music), pitch of a note that is perceived as the lowest Harmonic series (music)#Partial, partial present. In terms of a superposition of Sine wave, sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as 0, indicating the lowest frequency Zero-based numbering, counting from zero. In other contexts, it is more common to abbreviate it as 1, the first harmonic. (The second harmonic is then 2 = 2⋅1, etc.) According to Benward and Saker's ''Music: In Theory and Practice'': Explanation All sinusoidal and many non-sinusoidal waveforms repeat exactly over time – they are per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |