|
Matrix Norm
In the field of mathematics, norms are defined for elements within a vector space. Specifically, when the vector space comprises matrices, such norms are referred to as matrix norms. Matrix norms differ from vector norms in that they must also interact with matrix multiplication. Preliminaries Given a field \ K\ of either real or complex numbers (or any complete subset thereof), let \ K^\ be the -vector space of matrices with m rows and n columns and entries in the field \ K ~. A matrix norm is a norm on \ K^~. Norms are often expressed with double vertical bars (like so: \ \, A\, \ ). Thus, the matrix norm is a function \ \, \cdot\, : K^ \to \R^\ that must satisfy the following properties: For all scalars \ \alpha \in K\ and matrices \ A, B \in K^\ , * \, A\, \ge 0\ (''positive-valued'') * \, A\, = 0 \iff A=0_ (''definite'') * \left\, \alpha\ A \right\, = \left, \alpha \\ \left\, A\right\, \ (''absolutely homogeneous'') * \, A + B \, \le \, A \, + \, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Radius
''Spectral'' is a 2016 Hungarian-American military science fiction action film co-written and directed by Nic Mathieu. Written with Ian Fried (screenwriter), Ian Fried & George Nolfi, the film stars James Badge Dale as DARPA research scientist Mark Clyne, with Max Martini, Emily Mortimer, Clayne Crawford, and Bruce Greenwood in supporting roles. The film is set in a civil war-ridden Moldova as invisible entities slaughter any living being caught in their path. The film was released worldwide on December 9, 2016 on Netflix. On February 1, 2017, Netflix released a prequel graphic novel of the film called ''Spectral: Ghosts of War'' which was made available digitally through the website ComiXology. Plot DARPA researcher Mark Clyne is sent to a United States, US United States Armed Forces, military Air base, airbase on the outskirts of Chișinău, to consult his created line of hyperspectral imaging goggles issued to United States Army, US Army United States Army Special Forces, S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Matrix
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, Because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So if a_ denotes the entry in the ith row and jth column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero. Similarly in characteristic different from 2, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative. In linear algebra, a real symmetric matrix represents a self-adjoint operator represented in an orthonormal basis over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norm (mathematics)
In mathematics, a norm is a function (mathematics), function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the Origin (mathematics), origin: it Equivariant map, commutes with scaling, obeys a form of the triangle inequality, and zero is only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the #Euclidean norm, Euclidean norm, the #p-norm, 2-norm, or, sometimes, the magnitude or length of the vector. This norm can be defined as the square root of the inner product of a vector with itself. A seminorm satisfies the first two properties of a norm but may be zero for vectors other than the origin. A vector space with a specified norm is called a normed vector space. In a similar manner, a vector space with a seminorm is called a ''seminormed vector space''. The term pseudonorm has been used for several related meaning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermitian Matrix
In mathematics, a Hermitian matrix (or self-adjoint matrix) is a complex square matrix that is equal to its own conjugate transpose—that is, the element in the -th row and -th column is equal to the complex conjugate of the element in the -th row and -th column, for all indices and : A \text \quad \iff \quad a_ = \overline or in matrix form: A \text \quad \iff \quad A = \overline . Hermitian matrices can be understood as the complex extension of real symmetric matrices. If the conjugate transpose of a matrix A is denoted by A^\mathsf, then the Hermitian property can be written concisely as A \text \quad \iff \quad A = A^\mathsf Hermitian matrices are named after Charles Hermite, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of always having real eigenvalues. Other, equivalent notations in common use are A^\mathsf = A^\dagger = A^\ast, although in quantum mechanics, A^\ast typically means the complex conjugate onl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Matrix
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, Because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So if a_ denotes the entry in the ith row and jth column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero. Similarly in characteristic different from 2, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative. In linear algebra, a real symmetric matrix represents a self-adjoint operator represented in an orthonormal basis over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Radius
''Spectral'' is a 2016 Hungarian-American military science fiction action film co-written and directed by Nic Mathieu. Written with Ian Fried (screenwriter), Ian Fried & George Nolfi, the film stars James Badge Dale as DARPA research scientist Mark Clyne, with Max Martini, Emily Mortimer, Clayne Crawford, and Bruce Greenwood in supporting roles. The film is set in a civil war-ridden Moldova as invisible entities slaughter any living being caught in their path. The film was released worldwide on December 9, 2016 on Netflix. On February 1, 2017, Netflix released a prequel graphic novel of the film called ''Spectral: Ghosts of War'' which was made available digitally through the website ComiXology. Plot DARPA researcher Mark Clyne is sent to a United States, US United States Armed Forces, military Air base, airbase on the outskirts of Chișinău, to consult his created line of hyperspectral imaging goggles issued to United States Army, US Army United States Army Special Forces, S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consistent And Compatible Norms
In deductive logic, a consistent theory is one that does not lead to a logical contradiction. A theory T is consistent if there is no formula \varphi such that both \varphi and its negation \lnot\varphi are elements of the set of consequences of T. Let A be a set of closed sentences (informally "axioms") and \langle A\rangle the set of closed sentences provable from A under some (specified, possibly implicitly) formal deductive system. The set of axioms A is consistent when there is no formula \varphi such that \varphi \in \langle A \rangle and \lnot \varphi \in \langle A \rangle. A ''trivial'' theory (i.e., one which proves every sentence in the language of the theory) is clearly inconsistent. Conversely, in an explosive formal system (e.g., classical or intuitionistic propositional or first-order logics) every inconsistent theory is trivial. Consistency of a theory is a syntactic notion, whose semantic counterpart is satisfiability. A theory is satisfiable if it has a mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frobenius Norm
In the field of mathematics, norms are defined for elements within a vector space. Specifically, when the vector space comprises matrices, such norms are referred to as matrix norms. Matrix norms differ from vector norms in that they must also interact with matrix multiplication. Preliminaries Given a field \ K\ of either real or complex numbers (or any complete subset thereof), let \ K^\ be the -vector space of matrices with m rows and n columns and entries in the field \ K ~. A matrix norm is a norm on \ K^~. Norms are often expressed with double vertical bars (like so: \ \, A\, \ ). Thus, the matrix norm is a function \ \, \cdot\, : K^ \to \R^\ that must satisfy the following properties: For all scalars \ \alpha \in K\ and matrices \ A, B \in K^\ , * \, A\, \ge 0\ (''positive-valued'') * \, A\, = 0 \iff A=0_ (''definite'') * \left\, \alpha\ A \right\, = \left, \alpha \\ \left\, A\right\, \ (''absolutely homogeneous'') * \, A + B \, \le \, A \, + \, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Value Decomposition
In linear algebra, the singular value decomposition (SVD) is a Matrix decomposition, factorization of a real number, real or complex number, complex matrix (mathematics), matrix into a rotation, followed by a rescaling followed by another rotation. It generalizes the eigendecomposition of a square normal matrix with an orthonormal eigenbasis to any matrix. It is related to the polar decomposition#Matrix polar decomposition, polar decomposition. Specifically, the singular value decomposition of an m \times n complex matrix is a factorization of the form \mathbf = \mathbf, where is an complex unitary matrix, \mathbf \Sigma is an m \times n rectangular diagonal matrix with non-negative real numbers on the diagonal, is an n \times n complex unitary matrix, and \mathbf V^* is the conjugate transpose of . Such decomposition always exists for any complex matrix. If is real, then and can be guaranteed to be real orthogonal matrix, orthogonal matrices; in such contexts, the SVD ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
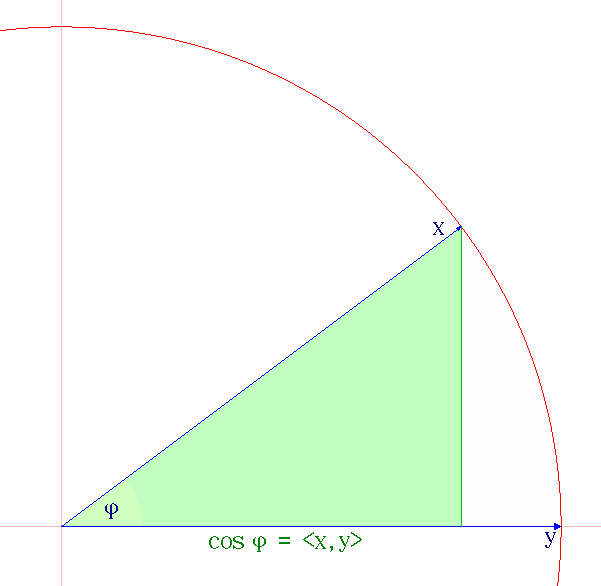
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the absolute value of the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics. Inner products of vectors can describe finite sums (via finite-dimensional vector spaces), infinite series (via vectors in sequence spaces), and integrals (via vectors in Hilbert spaces). The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |