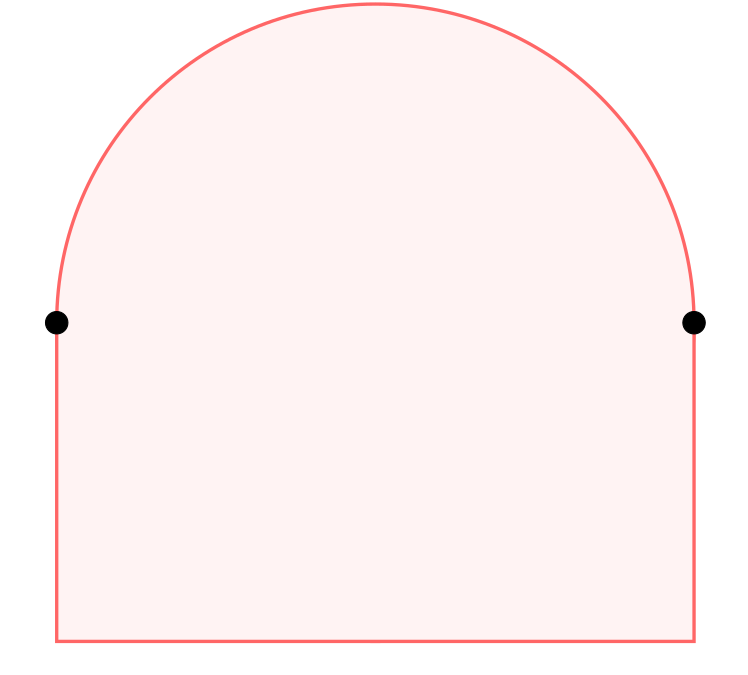
Exposed Face

picture info	Exposed Face In mathematics, most commonly in convex geometry, an extreme set or face of a set C\subseteq V in a vector space V is a subset F\subseteq C with the property that if for any two points x,y\in C some in-between point z=\theta x + (1-\theta) y,\theta\in ,1/math> lies in F, then we must have had x,y\in F. An extreme point of C is a point p\in C for which \ is a face. An exposed face of C is the subset of points of C where a linear functional achieves its minimum on C. Thus, if f is a linear functional on V and \alpha =\inf\>-\infty, then \ is an exposed face of C. An exposed point of C is a point p\in C such that \ is an exposed face. That is, f(p) > f(c) for all c\in C\setminus\. An exposed face is a face, but the converse is not true (see the figure). An exposed face of C is convex if C is convex. If F is a face of C\subseteq V, then E\subseteq F is a face of F if and only if E is a face of C. Competing definitions Some authors do not include C and/or \varnothing am ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Convex Geometry In mathematics, convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space. Convex sets occur naturally in many areas: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming, probability theory, game theory, etc. Classification According to the Mathematics Subject Classification MSC2010, the mathematical discipline ''Convex and Discrete Geometry'' includes three major branches: * general convexity * polytopes and polyhedra * discrete geometry (though only portions of the latter two are included in convex geometry). General convexity is further subdivided as follows: axiomatic and generalized convexity convex sets without dimension restrictions convex sets in topological vector spaces convex sets in 2 dimensions (including convex curves) convex sets in 3 dimensions (including convex surfaces) convex sets in ''n'' dimensions (including convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Vector Space In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called scalar (mathematics), ''scalars''. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. Real vector spaces and complex vector spaces are kinds of vector spaces based on different kinds of scalars: real numbers and complex numbers. Scalars can also be, more generally, elements of any field (mathematics), field. Vector spaces generalize Euclidean vectors, which allow modeling of Physical quantity, physical quantities (such as forces and velocity) that have not only a Magnitude (mathematics), magnitude, but also a Orientation (geometry), direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix (mathematics), matrices, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Extreme Point In mathematics, an extreme point of a convex set S in a Real number, real or Complex number, complex vector space is a point in S that does not lie in any open line segment joining two points of S. The extreme points of a line segment are called its ''endpoint (geometry), endpoints''. In linear programming problems, an extreme point is also called ''vertex (geometry), vertex'' or ''corner point'' of S. Definition Throughout, it is assumed that X is a Real number, real or Complex number, complex vector space. For any p, x, y \in X, say that p x and y if x \neq y and there exists a 0 < t < 1 such that $p = t x + (1-t) y.$ If $K$ is a subset of $X$ and $p \in K,$ then $p$ is called an of $K$ if it does not lie between any two points of $K.$ That is, if there does exist $x, y \in K$ and $0 < t < 1$ such that $x \neq y$ and $p = t x + (1-t) y.$ The s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Exposed Face In mathematics, most commonly in convex geometry, an extreme set or face of a set C\subseteq V in a vector space V is a subset F\subseteq C with the property that if for any two points x,y\in C some in-between point z=\theta x + (1-\theta) y,\theta\in ,1/math> lies in F, then we must have had x,y\in F. An extreme point of C is a point p\in C for which \ is a face. An exposed face of C is the subset of points of C where a linear functional achieves its minimum on C. Thus, if f is a linear functional on V and \alpha =\inf\>-\infty, then \ is an exposed face of C. An exposed point of C is a point p\in C such that \ is an exposed face. That is, f(p) > f(c) for all c\in C\setminus\. An exposed face is a face, but the converse is not true (see the figure). An exposed face of C is convex if C is convex. If F is a face of C\subseteq V, then E\subseteq F is a face of F if and only if E is a face of C. Competing definitions Some authors do not include C and/or \varnothing am ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Exposed Point In mathematics, an exposed point of a convex set C is a point x\in C at which some continuous linear functional attains its strict maximum over C. Such a functional is then said to ''expose'' x. There can be many exposing functionals for x. The set of exposed points of C is usually denoted \exp(C). A stronger notion is that of ''strongly exposed point'' of C which is an exposed point x \in C such that some exposing functional f of x attains its strong maximum over C at x, i.e. for each sequence (x_n) \subset C we have the following implication: f(x_n) \to \max f(C) \Longrightarrow \, x_n -x\, \to 0. The set of all strongly exposed points of C is usually denoted \operatorname\exp(C). There are two weaker notions, that of extreme point and that of support point of C. See also * Exposed face In mathematics, most commonly in convex geometry, an extreme set or face of a set C\subseteq V in a vector space V is a subset F\subseteq C with the property that if for any two points x ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Convex Set In geometry, a set of points is convex if it contains every line segment between two points in the set. For example, a solid cube (geometry), cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary (topology), boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval (mathematics), interval with the property that its epigraph (mathematics), epigraph (the set of points on or above the graph of a function, graph of the function) is a convex set. Convex minimization is a subfield of mathematical optimization, optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Vector Topology In mathematics, a topological vector space (also called a linear topological space and commonly abbreviated TVS or t.v.s.) is one of the basic structures investigated in functional analysis. A topological vector space is a vector space that is also a topological space with the property that the vector space operations (vector addition and scalar multiplication) are also Continuous function, continuous functions. Such a topology is called a and every topological vector space has a Uniform space, uniform topological structure, allowing a notion of uniform convergence and Complete topological vector space, completeness. Some authors also require that the space is a Hausdorff space (although this article does not). One of the most widely studied categories of TVSs are locally convex topological vector spaces. This article focuses on TVSs that are not necessarily locally convex. Other well-known examples of TVSs include Banach spaces, Hilbert spaces and Sobolev spaces. Many topological ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]