|
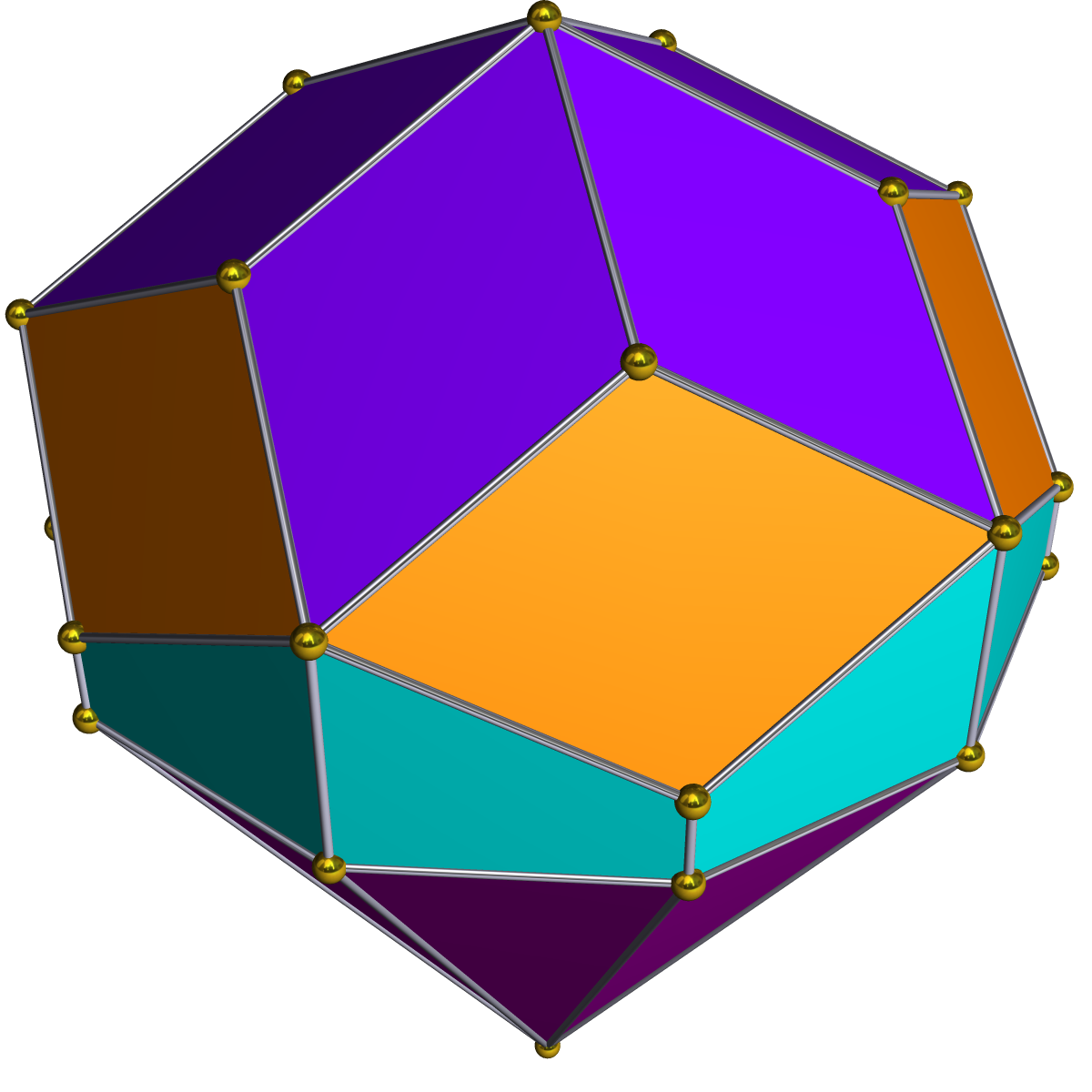
Elongated Pentagonal Rotunda
In geometry, the elongated pentagonal rotunda is one of the Johnson solids (''J''21). As the name suggests, it can be constructed by elongating a pentagonal rotunda (''J''6) by attaching a decagonal prism to its base. It can also be seen as an elongated pentagonal orthobirotunda (''J''42) with one pentagonal rotunda removed. Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal rotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 22, 2010. V=\frac\left(45+17\sqrt+30\sqrt\right)a^3\approx14.612...a^3 A=\frac\left(20+\sqrt\right)a^2\approx32.3472...a^2 Dual polyhedron The dual of the elongated pentagonal rotunda has 30 faces: 10 isos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, solids with such a property: the first solids are the Pyramid (geometry), pyramids, Cupola (geometry), cupolas, and a Rotunda (geometry), rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. Definition and background A Johnson solid is a convex polyhedron whose faces are all regular polygons. The convex polyhedron means as bounded intersections of finitely many Half-space (geometry), half-spaces, or as the convex hull of finitely many points. Although there is no restriction that any given regular polygon cannot be a face of a Johnson solid, some authors required that Johnson solids are not Uniform polyhedron, uniform. This means that a Johnson solid is not a Platonic solid, Arc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Orthobirotunda
In geometry, the elongated pentagonal orthobirotunda is one of the Johnson solids (). Its Conway polyhedron notation iat5jP5 As the name suggests, it can be constructed by elongating a pentagonal orthobirotunda () by inserting a decagonal prism between its congruent halves. Rotating one of the pentagonal rotundae () through 36 degrees before inserting the prism yields the elongated pentagonal gyrobirotunda (). Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal orthobirotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 26, 2010. :V=\frac\left(45+17\sqrt+15\sqrt\right)a^3\approx21.5297...a^3 :A=\left(10+\sqrt\right)a^2\approx39 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
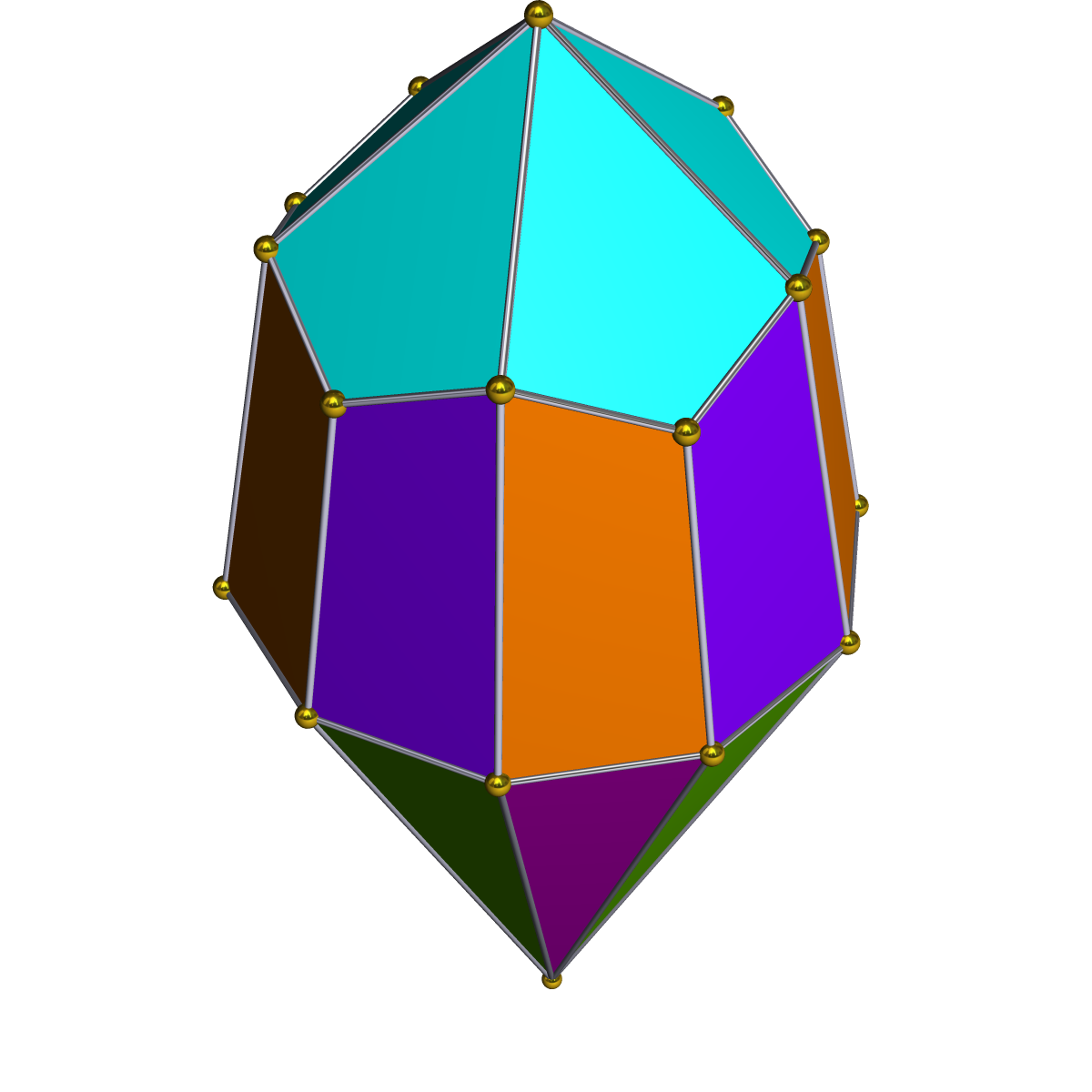
Dual Elongated Pentagonal Rotunda
Dual or Duals may refer to: Paired/two things * Dual (mathematics), a notion of paired concepts that mirror one another ** Dual (category theory), a formalization of mathematical duality *** see more cases in :Duality theories * Dual number, a number system used in automatic differentiation * Dual (grammatical number) Dual ( abbreviated ) is a grammatical number that some languages use in addition to singular and plural. When a noun or pronoun appears in dual form, it is interpreted as referring to precisely two of the entities (objects or persons) identifie ..., a grammatical category used in some languages * Dual county, a Gaelic games county which competes in both Gaelic football and hurling * Dual diagnosis, a psychiatric diagnosis of co-occurrence of substance abuse and a mental problem * Dual fertilization, simultaneous application of a P-type and N-type fertilizer * Dual impedance, electrical circuits that are the dual of each other * Dual SIM cellphone supporting use o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wolfram Alpha
WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on May 15, 2009, at 7:00 pm CDT with a live broadcast on Justin.tv. The plan was to publicly launch the service a few hours later. However, there were issues due to extreme load. The service officially launched on May 18, 2009, receiving mixed reviews. The engine is based on Wolfram's earlier product Wolfram Mathematica, a technical computing platform. The coding is written in Wolfram Language, a general multi-paradigm programming language, and implemented in Mathematica. WolframAlpha gathers data from academic and commercial websites such as the CIA's ''The World Factbook'', the United States Geological Survey, a Cornell University Library publication called ''All About Birds'', '' Chambers Biographical Dictionary'', Dow Jones, the ''Cat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stephen Wolfram
Stephen Wolfram ( ; born 29 August 1959) is a British-American computer scientist, physicist, and businessman. He is known for his work in computer algebra and theoretical physics. In 2012, he was named a fellow of the American Mathematical Society. As a businessman, he is the founder and CEO of the software company Wolfram Research, where he works as chief designer of Mathematica and the Wolfram Alpha answer engine. Early life Family Stephen Wolfram was born in London in 1959 to Hugo and Sybil Wolfram, both German Jewish refugees to the United Kingdom. His maternal grandmother was British psychoanalyst Kate Friedlander. Wolfram's father, Hugo Wolfram, was a textile manufacturer and served as managing director of the Lurex Company—makers of the fabric Lurex. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex polygon, convex'' or ''star polygon, star''. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties These properties apply to all regular polygons, whether convex or star polygon, star: *A regular ''n''-sided polygon has rotational symmetry of order ''n''. *All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. *Together with the property of equal-length sides, this implies that every regular polygon also h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face (geometry)
In solid geometry, a face is a flat surface (a Plane (geometry), planar region (mathematics), region) that forms part of the boundary of a solid object. For example, a cube has six faces in this sense. In more modern treatments of the geometry of polyhedra and higher-dimensional polytopes, a "face" is defined in such a way that it may have any dimension. The vertices, edges, and (2-dimensional) faces of a polyhedron are all faces in this more general sense. Polygonal face In elementary geometry, a face is a polygon on the boundary of a polyhedron. (Here a "polygon" should be viewed as including the 2-dimensional region inside it.) Other names for a polygonal face include polyhedron side and Euclidean plane ''tessellation, tile''. For example, any of the six square (geometry), squares that bound a cube is a face of the cube. Sometimes "face" is also used to refer to the 2-dimensional features of a 4-polytope. With this meaning, the 4-dimensional tesseract has 24 square faces, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region (e.g., bounding volume). In ancient times, volume was measured using similar-shaped natural containers. Later on, standardized containers were used. Some simple three-dimensional shapes can have their volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship between given quantities. The plural of ''formula'' can be either ''formulas'' (from the most common English plural noun form) or, under the influence of scientific Latin, ''formulae'' (from the original Latin). In mathematics In mathematics, a formula generally refers to an equation or inequality relating one mathematical expression to another, with the most important ones being mathematical theorems. For example, determining the volume of a sphere requires a significant amount of integral calculus or its geometrical analogue, the method of exhaustion. However, having done this once in terms of some parameter (the radius for example), mathematicians have produced a formula to describe the volume of a sphere in terms of its radius: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decagonal Prism
In geometry, a prism is a polyhedron comprising an polygon base, a second base which is a translated copy (rigidly moved without rotation) of the first, and other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's ''Elements''. Euclid defined the term in Book XI as "a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms". However, this definition has been criticized for not being specific enough in regard to the nature of the bases (a cause of some confusion amongst generations of later geometry writers). Oblique vs right An oblique prism is a prism in which the joining edges and faces are ''not perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Cupola
In geometry, the elongated pentagonal cupola is one of the Johnson solids (). As the name suggests, it can be constructed by elongating a pentagonal cupola () by attaching a decagonal prism to its base. The solid can also be seen as an elongated pentagonal orthobicupola () with its "lid" (another pentagonal cupola) removed. Formulas The following formulas for the volume and surface area can be used if all face (geometry), faces are regular polygon, regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal cupola from Wolfram Alpha. Retrieved July 22, 2010. :V=\left(\frac\left(5+4\sqrt+15\sqrt\right)\right)a^3\approx10.0183...a^3 :A=\left(\frac\left(60+\sqrt\right)\right)a^2\approx26.5797...a^2 Dual polyhedron The dual of the elongated pentagonal cupola has 25 faces: 10 isosceles triangles, 5 kites, and 10 quadrilaterals. References External links * {{Johnson solids navigator Johnson solids ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |