|
Elongated Pentagonal Orthobirotunda
In geometry, the elongated pentagonal orthobirotunda is one of the Johnson solids (). Its Conway polyhedron notation iat5jP5 As the name suggests, it can be constructed by elongating a pentagonal orthobirotunda () by inserting a decagonal prism between its congruent halves. Rotating one of the pentagonal rotundae () through 36 degrees before inserting the prism yields the elongated pentagonal gyrobirotunda (). Formulae The following formulae for volume and surface area The surface area of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc ... can be used if all faces are regular, with edge length ''a'': Stephen Wolfram,Elongated pentagonal orthobirotunda from Wolfram Alpha. Retrieved July 26, 2010. :V=\frac\left(45+17\sqrt+15\sqrt\right)a^3\approx21.5297...a^3 :A=\left(10+\sqrt\right)a^2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides ( ); it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform (i.e., not Platonic solid, Archimedean solid, uniform prism, or uniform antiprism) before they refer to it as a “Johnson solid”. As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid () is an example that has a degree-5 vertex. Although there is no obvious restriction that any given regular polygon cannot be a face of a Johnson solid, it turns out that the face ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decagonal Prism
In geometry, the decagonal prism is the eighth in the infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra. The decagonal prism has 12 faces, 30 edges, and 20 vertices, so, it is a dodecahedron (while the term is usually applied to regular dodecahedron or rhombic dodecahedron.). If faces are all regular, it is a semiregular or prismatic uniform polyhedron. Uses The decagonal prism exists as cells in two four-dimensional uniform 4-polytope In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons. There are 47 non-prismatic convex uniform 4-polytopes. There ...s: Related polyhedra External links * 3-d model of a Decagonal Prism Prismatoid polyhedra Zonohedra {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stephen Wolfram
Stephen Wolfram (; born 29 August 1959) is a British-American computer scientist, physicist, and businessman. He is known for his work in computer science, mathematics, and theoretical physics. In 2012, he was named a fellow of the American Mathematical Society. He is currently an adjunct professor at the University of Illinois Department of Computer Science. As a businessman, he is the founder and CEO of the software company Wolfram Research where he works as chief designer of Mathematica and the Wolfram Alpha answer engine. Early life Family Stephen Wolfram was born in London in 1959 to Hugo and Sybil Wolfram, both German Jewish refugees to the United Kingdom. His maternal grandmother was British psychoanalyst Kate Friedlander. Wolfram's father, Hugo Wolfram, was a textile manufacturer and served as managing director of the Lurex Company—makers of the fabric Lurex. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is direct equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Regular polygons may be either convex, star or skew. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a straight line), if the edge length is fixed. General properties ''These properties apply to all regular polygons, whether convex or star.'' A regular ''n''-sided polygon has rotational symmetry of order ''n''. All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. Together with the property of equal-length sides, this implies that every regular polygon also has an inscribed circle or incircle that is tangent to every side at the midpoint. Thus a regular polygon is a tangen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Faces (geometry)
In solid geometry, a face is a flat surface (a planar region) that forms part of the boundary of a solid object; a three-dimensional solid bounded exclusively by faces is a ''polyhedron''. In more technical treatments of the geometry of polyhedra and higher-dimensional polytopes, the term is also used to mean an element of any dimension of a more general polytope (in any number of dimensions).. Polygonal face In elementary geometry, a face is a polygon on the boundary of a polyhedron. Other names for a polygonal face include polyhedron side and Euclidean plane ''tile''. For example, any of the six squares that bound a cube is a face of the cube. Sometimes "face" is also used to refer to the 2-dimensional features of a 4-polytope. With this meaning, the 4-dimensional tesseract has 24 square faces, each sharing two of 8 cubic cells. Number of polygonal faces of a polyhedron Any convex polyhedron's surface has Euler characteristic :V - E + F = 2, where ''V'' is the number of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is the Minkows ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. In ancient times, volume is measured using similar-shaped natural containers and later on, standardized containers. Some simple three-dimensional shapes can have its volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape's boundary. Zero-, one- and two-dimensional objects have no volume; in fourth and higher dimensions, an analogous concept to the no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a '' chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship between given quantities. The plural of ''formula'' can be either ''formulas'' (from the most common English plural noun form) or, under the influence of scientific Latin, ''formulae'' (from the original Latin). In mathematics In mathematics, a formula generally refers to an identity which equates one mathematical expression to another, with the most important ones being mathematical theorems. Syntactically, a formula (often referred to as a '' well-formed formula'') is an entity which is constructed using the symbols and formation rules of a given logical language. For example, determining the volume of a sphere requires a significant amount of integral calculus or its geometrical analogue, the method of exhaustion. However, ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Rotunda
In geometry, the pentagonal rotunda is one of the Johnson solids (). It can be seen as half of an icosidodecahedron, or as half of a pentagonal orthobirotunda. It has a total of 17 faces. Formulae The following formulae for volume, surface area, circumradius, and height are valid if all faces are regular The term regular can mean normal or in accordance with rules. It may refer to: People * Moses Regular (born 1971), America football player Arts, entertainment, and media Music * "Regular" (Badfinger song) * Regular tunings of stringed instrum ..., with edge length ''a'': :V=\left(\frac\left(45+17\sqrt\right)\right)a^3\approx6.91776...a^3 :\begin A&=\left(\frac\sqrt\right)a^2 \\ &=\left(\frac\left(5\sqrt+\sqrt\right)\right)a^2\approx22.3472...a^2 \end :R=\left(\frac\left(1+\sqrt\right)\right)a\approx1.61803...a :H=\left(\sqrt\right)a\approx1.37638...a Dual polyhedron The dual of the pentagonal rotunda has 20 faces: 10 triangular, 5 rhombic, and 5 kites. References E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Orthobirotunda
In geometry, the pentagonal orthobirotunda is one of the Johnson solids (). It can be constructed by joining two pentagonal rotundae () along their decagonal faces, matching like faces. Related polyhedra The pentagonal orthobirotunda is also related to an Archimedean solid, the icosidodecahedron, which can also be called a ''pentagonal gyrobirotunda'', similarly created by two pentagonal rotunda but with a 36-degree rotation Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional .... External links * Johnson solids {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Gyrocupolarotunda
In geometry, the elongated pentagonal gyrocupolarotunda is one of the Johnson solids (). As the name suggests, it can be constructed by elongating a pentagonal gyrocupolarotunda () by inserting a decagonal prism between its halves. Rotating either the pentagonal cupola () or the pentagonal rotunda () through 36 degrees before inserting the prism yields an elongated pentagonal orthocupolarotunda (). Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'': Stephen Wolfram,Elongated pentagonal gyrocupolarotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It answers factual queries by computing answers from externally sourced data. WolframAlpha was released on May 18, 2009 and is based on Wolfram's earlier product Wolfram Mathe .... Retrieved July 25, 2010. :V=\frac\left(11+5\sqrt+6\sqrt\right)a^3\approx16.936...a^3 :A=\frac\left(60+\sqrt\right)a^2\approx33.53 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
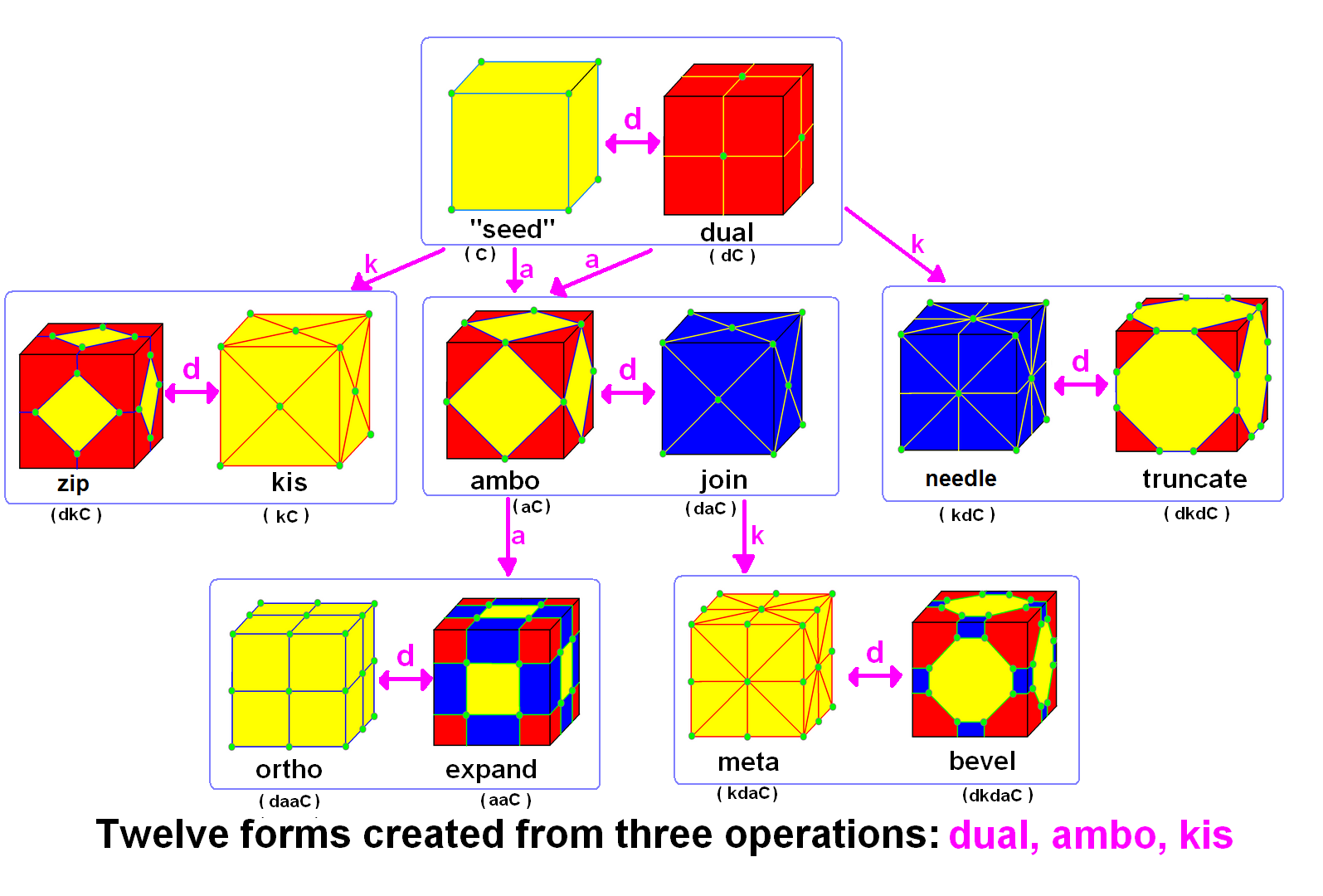
Conway Polyhedron Notation
In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is (topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), (snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the Archimedean and Cat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |