|
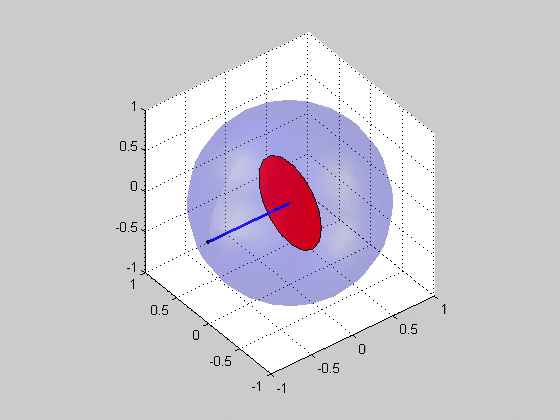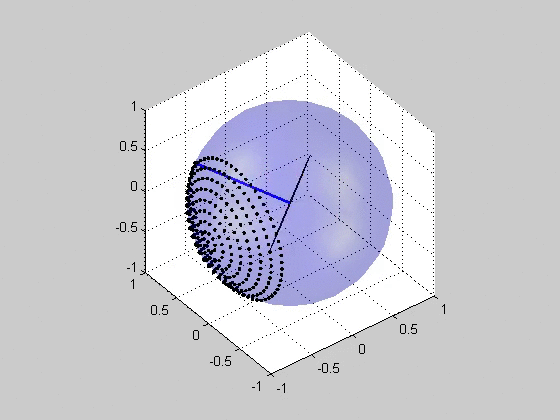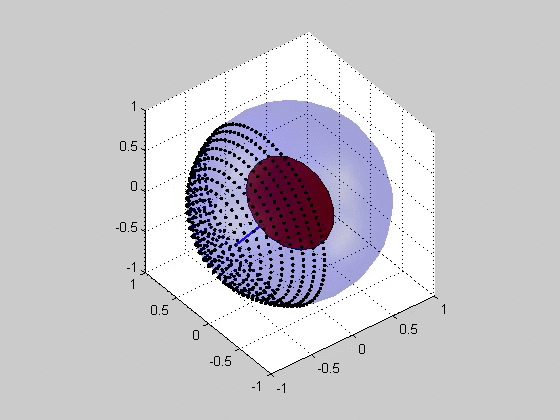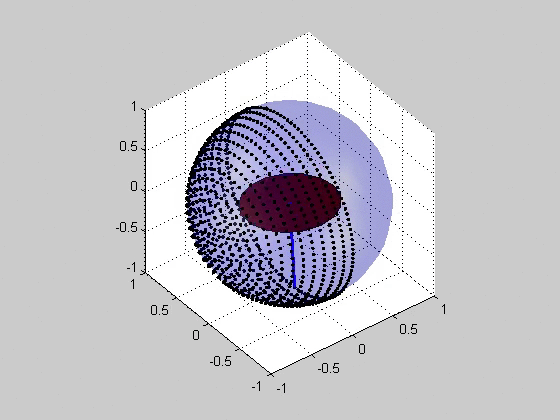
Critical Plane Analysis
Critical plane analysis refers to the analysis of Stress (mechanics), stresses or Deformation (mechanics), strains as they are experienced by a particular plane in a material, as well as the identification of which plane is likely to experience the most extreme damage mechanics, damage. Critical plane analysis is widely used in engineering to account for the effects of cyclic, multiaxial load histories on the fatigue (material), fatigue life of materials and structures. When a structure is under cyclic multiaxial loading, it is necessary to use multiaxial fatigue criteria that account for the multiaxial loading. If the cyclic multiaxial loading is nonproportional it is mandatory to use a proper multiaxial fatigue criteria. The multiaxial criteria based on the Critical Plane Method are the most effective criteria. For the plane stress case, the orientation of the plane may be specified by an angle in the plane, and the stresses and strains acting on this plane may be computed via Mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity that describes forces present during deformation. For example, an object being pulled apart, such as a stretched elastic band, is subject to ''tensile'' stress and may undergo elongation. An object being pushed together, such as a crumpled sponge, is subject to ''compressive'' stress and may undergo shortening. The greater the force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Stress has dimension of force per area, with SI units of newtons per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while ''strain'' is the measure of the relative deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushes on the particles immediately below it. When a liquid is in a closed container under pressure, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation (mechanics)
In physics and continuum mechanics, deformation is the change in the shape (geometry), shape or size of an object. It has dimension (physics), dimension of length with SI unit of metre (m). It is quantified as the residual displacement (geometry), displacement of particles in a non-rigid body, from an configuration to a configuration, excluding the body's average translation (physics), translation and rotation (its rigid transformation). A ''configuration'' is a set containing the position (geometry), positions of all particles of the body. A deformation can occur because of structural load, external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. In a continuous body, a ''deformation field'' results from a Stress (physics), stress field due to applied forces or because of some changes in the conditions of the body. The relation between stre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Damage Mechanics
Damage mechanics is concerned with the representation, or modeling, of damage of materials that is suitable for making engineering predictions about the initiation, propagation, and fracture of materials without resorting to a microscopic description that would be too complex for practical engineering analysis. Damage mechanics illustrates the typical engineering approach to model complex phenomena. To quote Dusan Krajcinovic, "It is often argued that the ultimate task of engineering research is to provide not so much a better insight into the examined phenomenon but to supply a rational predictive tool applicable in design." Damage mechanics is a topic of applied mechanics that relies heavily on continuum mechanics. Most of the work on damage mechanics uses state variables to represent the ''effects'' of damage on the stiffness and remaining life of the material that is damaging as a result of thermomechanical load and ageing. The state variables may be measurable, e.g., crack den ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fatigue (material)
In materials science, fatigue is the initiation and propagation of cracks in a material due to cyclic loading. Once a fatigue crack has initiated, it grows a small amount with each loading cycle, typically producing striations on some parts of the fracture surface. The crack will continue to grow until it reaches a critical size, which occurs when the stress intensity factor of the crack exceeds the fracture toughness of the material, producing rapid propagation and typically complete fracture of the structure. Fatigue has traditionally been associated with the failure of metal components which led to the term metal fatigue. In the nineteenth century, the sudden failing of metal railway axles was thought to be caused by the metal crystallising because of the brittle appearance of the fracture surface, but this has since been disproved. Most materials, such as composites, plastics and ceramics, seem to experience some sort of fatigue-related failure. To aid in predicting the f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Stress
In continuum mechanics, a material is said to be under plane stress if the stress (mechanics), stress vector is zero across a particular plane. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2 (representable as a 2×2 matrix rather than 3×3). A related notion, plane strain, is often applicable to very thick members. Plane stress typically occurs in thin flat plates that are acted upon only by load forces that are parallel to them. In certain situations, a gently curved thin plate may also be assumed to have plane stress for the purpose of stress analysis. This is the case, for example, of a thin-walled cylinder filled with a fluid under pressure. In such cases, stress components perpendicular to the plate are negligible compared to those parallel to it. In other situations, however, the bending stress of a thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mohr's Circle
Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor. Mohr's circle is often used in calculations relating to mechanical engineering for materials' strength, geotechnical engineering for strength of soils, and structural engineering for strength of built structures. It is also used for calculating stresses in many planes by reducing them to vertical and horizontal components. These are called principal planes in which principal stresses are calculated; Mohr's circle can also be used to find the principal planes and the principal stresses in a graphical representation, and is one of the easiest ways to do so. After performing a stress analysis on a material body assumed as a continuum, the components of the Cauchy stress tensor at a particular material point are known with respect to a coordinate system. The Mohr circle is then used to determine graphically the stress components acting on a rotated coordinate sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Stress Tensor
In continuum mechanics, the Cauchy stress tensor (symbol \boldsymbol\sigma, named after Augustin-Louis Cauchy), also called true stress tensor or simply stress tensor, completely defines the state of stress at a point inside a material in the deformed state, placement, or configuration. The second order tensor consists of nine components \sigma_ and relates a unit-length direction vector e to the ''traction vector'' T(e) across an imaginary surface perpendicular to e: :\mathbf^ = \mathbf e \cdot\boldsymbol\quad \text \quad T_^= \sum_\sigma_e_i. The SI base units of both stress tensor and traction vector are newton per square metre (N/m2) or pascal (Pa), corresponding to the stress scalar. The unit vector is dimensionless. The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle for stress. The Cauchy stress tensor is used for stress analysis of mater ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Critical Plane Analysis
Critical plane analysis refers to the analysis of Stress (mechanics), stresses or Deformation (mechanics), strains as they are experienced by a particular plane in a material, as well as the identification of which plane is likely to experience the most extreme damage mechanics, damage. Critical plane analysis is widely used in engineering to account for the effects of cyclic, multiaxial load histories on the fatigue (material), fatigue life of materials and structures. When a structure is under cyclic multiaxial loading, it is necessary to use multiaxial fatigue criteria that account for the multiaxial loading. If the cyclic multiaxial loading is nonproportional it is mandatory to use a proper multiaxial fatigue criteria. The multiaxial criteria based on the Critical Plane Method are the most effective criteria. For the plane stress case, the orientation of the plane may be specified by an angle in the plane, and the stresses and strains acting on this plane may be computed via Mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sines Rule
Sines () is a town and a municipality in Portugal. The municipality, divided into two parishes, has around 14,214 inhabitants (2021) in an area of . Sines holds an important oil refinery and several petrochemical industries. It is also a popular beach spot and the main fishing harbour of Alentejo region. The municipality is bordered to the north and east by the municipality of Santiago do Cacém, south by Odemira and west by the Atlantic Ocean. The coastline of the city, south of São Torpes, is part of the Southwest Alentejo and Vicentine Coast Natural Park. History Vestiges of a few settlements have today been discovered in archaeological sites, such as Palmeirinha and Quitéria, that attest to the age of human settlements in Sines. Arnaldo Soledade (1981) noted that these Visigoths, identified as ''Cinetos'', may have been the original civilization that gave rise to the community, suggesting the local toponymy may have derived from this; ''Cinetos'', to Cines and, finally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Stress Tensor
In continuum mechanics, the Cauchy stress tensor (symbol \boldsymbol\sigma, named after Augustin-Louis Cauchy), also called true stress tensor or simply stress tensor, completely defines the state of stress at a point inside a material in the deformed state, placement, or configuration. The second order tensor consists of nine components \sigma_ and relates a unit-length direction vector e to the ''traction vector'' T(e) across an imaginary surface perpendicular to e: :\mathbf^ = \mathbf e \cdot\boldsymbol\quad \text \quad T_^= \sum_\sigma_e_i. The SI base units of both stress tensor and traction vector are newton per square metre (N/m2) or pascal (Pa), corresponding to the stress scalar. The unit vector is dimensionless. The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle for stress. The Cauchy stress tensor is used for stress analysis of mater ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strain Energy Density Function
A strain energy density function or stored energy density function is a scalar (mathematics), scalar-valued function (mathematics), function that relates the strain energy density of a material to the deformation gradient. : W = \hat(\boldsymbol) = \hat(\boldsymbol^T\cdot\boldsymbol) =\bar(\boldsymbol) = \bar(\boldsymbol^\cdot\boldsymbol)=\tilde(\boldsymbol,\boldsymbol) Equivalently, : W = \hat(\boldsymbol) = \hat(\boldsymbol^T\cdot\boldsymbol\cdot\boldsymbol) =\tilde(\boldsymbol,\boldsymbol) where \boldsymbol is the (two-point) deformation gradient tensor, \boldsymbol is the Finite strain theory#The_right_Cauchy–Green_deformation_tensor, right Cauchy–Green deformation tensor, \boldsymbol is the Finite strain theory#The_left_Cauchy–Green_or_Finger_deformation_tensor, left Cauchy–Green deformation tensor, and \boldsymbol is the rotation tensor from the polar decomposition of \boldsymbol. For an anisotropic material, the strain energy density function \hat(\bolds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crack Closure
Crack closure is a phenomenon in fatigue loading, where the opposing faces of a crack remain in contact even with an external load acting on the material. As the load is increased, a critical value will be reached at which time the crack becomes ''open''. Crack closure occurs from the presence of material propping open the crack faces and can arise from many sources including plastic deformation or phase transformation during crack propagation, corrosion of crack surfaces, presence of fluids in the crack, or roughness at cracked surfaces. Description During cyclic loading, a crack will open and close causing the crack tip opening displacement (CTOD) to vary cyclically in phase with the applied force. If the loading cycle includes a period of negative force or stress ratio R (i.e. R < 0), the CTOD will remain equal to zero as the crack faces are pressed together. However, it was discovered that the CTOD can also be zero at other times even when the applied force is positi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |