|
Coriolis Parameter
The Coriolis frequency ''ƒ'', also called the Coriolis parameter or Coriolis coefficient, is equal to twice the rotation rate ''Ω'' of the Earth multiplied by the sine of the latitude \varphi. f = 2 \Omega \sin \varphi.\, The rotation rate of the Earth (''Ω'' = 7.2921 × 10−5 rad/s) can be calculated as 2''π'' / ''T'' radians per second, where ''T'' is the rotation period of the Earth which is one ''sidereal'' day (23 h 56 min 4.1 s). In the midlatitudes, the typical value for f is about 10−4 rad/s. Inertial oscillations on the surface of the Earth have this frequency. These oscillations are the result of the Coriolis effect. Explanation Consider a body (for example a fixed volume of atmosphere) moving along at a given latitude \varphi at velocity v in the Earth's rotating reference frame. In the local reference frame of the body, the vertical direction is parallel to the radial vector poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound and light waves, the posit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Longitudes
Longitude (, ) is a geographic coordinate that specifies the east-west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians are imaginary semicircular lines running from pole to pole that connect points with the same longitude. The prime meridian defines 0° longitude; by convention the International Reference Meridian for the Earth passes near the Royal Observatory in Greenwich, south-east London on the island of Great Britain. Positive longitudes are east of the prime meridian, and negative ones are west. Because of the Earth's rotation, there is a close connection between longitude and time measurement. Scientifically precise local time varies with longitude: a difference of 15° longitude corresponds to a one-hour difference in local time, due to the differing position in relation to the Sun. Comparing local time to an absolute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Atmospheric Dynamics
Meteorology is the scientific study of the Earth's atmosphere and short-term atmospheric phenomena (i.e. weather), with a focus on weather forecasting. It has applications in the military, aviation, energy production, transport, agriculture, construction, weather warnings and disaster management. Along with climatology, atmospheric physics and atmospheric chemistry, meteorology forms the broader field of the atmospheric sciences. The interactions between Earth's atmosphere and its oceans (notably El Niño and La Niña) are studied in the interdisciplinary field of hydrometeorology. Other interdisciplinary areas include biometeorology, space weather and planetary meteorology. Marine weather forecasting relates meteorology to maritime and coastal safety, based on atmospheric interactions with large bodies of water. Meteorologists study List of meteorological phenomena, meteorological phenomena driven by solar radiation, Earth's rotation, ocean currents and other factors. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Rossby-gravity Waves
Rossby-gravity waves are equatorially trapped waves (much like Kelvin waves), meaning that they rapidly decay as their distance increases away from the equator (so long as the Brunt–Vaisala frequency does not remain constant). These waves have the same trapping scale as Kelvin waves, more commonly known as the equatorial Rossby deformation radius.Gill, Adrian E., 1982: ''Atmosphere-Ocean Dynamics,'' International Geophysics Series, Volume 30, Academic Press, 662 pp. They always carry energy eastward, but their 'crests' and 'troughs' may propagate westward if their periods are long enough. Derivation The eastward speed of propagation of these waves can be derived for an inviscid slowly moving layer of fluid of uniform depth H.Zhang, Dalin, 2008: Personal Communication, “Waves in Rotating, Homogeneous Fluids,” University of Maryland, College Park. Because the Coriolis parameter (''f'' = 2Ω sin(''θ'') where Ω is the angular velocity of the earth, 7.2921&n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Beta Plane
In geophysical fluid dynamics, an approximation whereby the Coriolis parameter, ''f'', is set to vary linearly in space is called a beta plane approximation. On a rotating sphere such as the Earth, ''f'' varies with the sine of latitude; in the so-called f-plane approximation, this variation is ignored, and a value of ''f'' appropriate for a particular latitude is used throughout the domain. This approximation can be visualized as a tangent plane touching the surface of the sphere at this latitude. A more accurate model is a linear Taylor series approximation to this variability about a given latitude \phi_0: f = f_0 + \beta y, where f_0 is the Coriolis parameter at \phi_0, \beta = (\mathrmf/\mathrmy), _ = 2\Omega\cos(\phi_0)/a is the Rossby parameter, y is the meridional distance from \phi_0, \Omega is the angular rotation rate of the Earth, and a is the Earth's radius. In analogy with the f-plane, this approximation is termed the beta plane, even though it no longer describe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Rossby Waves
Rossby waves, also known as planetary waves, are a type of inertial wave naturally occurring in rotating fluids. They were first identified by Sweden-born American meteorologist Carl-Gustaf Arvid Rossby in the Earth's atmosphere in 1939. They are observed in the atmospheres and oceans of Earth and other planets, owing to the rotation of Earth or of the planet involved. Atmospheric Rossby waves on Earth are giant meanders in high-altitude winds that have a major influence on weather. These waves are associated with pressure systems and the jet stream (especially around the Polar vortex, polar vortices). Oceanic Rossby waves move along the thermocline: the boundary between the warm upper layer and the cold deeper part of the ocean. Rossby wave types Atmospheric waves Atmospheric Rossby waves result from the conservation of potential vorticity and are influenced by the Coriolis force and pressure gradient. The image on the left sketches fundamental principles of the wave, e.g., its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Rossby Parameter
The Rossby parameter (or simply beta \beta) is a number used in geophysics and meteorology which arises due to the meridional variation of the Coriolis force caused by the spherical shape of the Earth. It is important in the generation of Rossby waves. The Rossby parameter \beta is given by for Atmospheric Science Mesoscale Dynamics (MEA 713). . Accessed 14 July 2007. : where is the , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
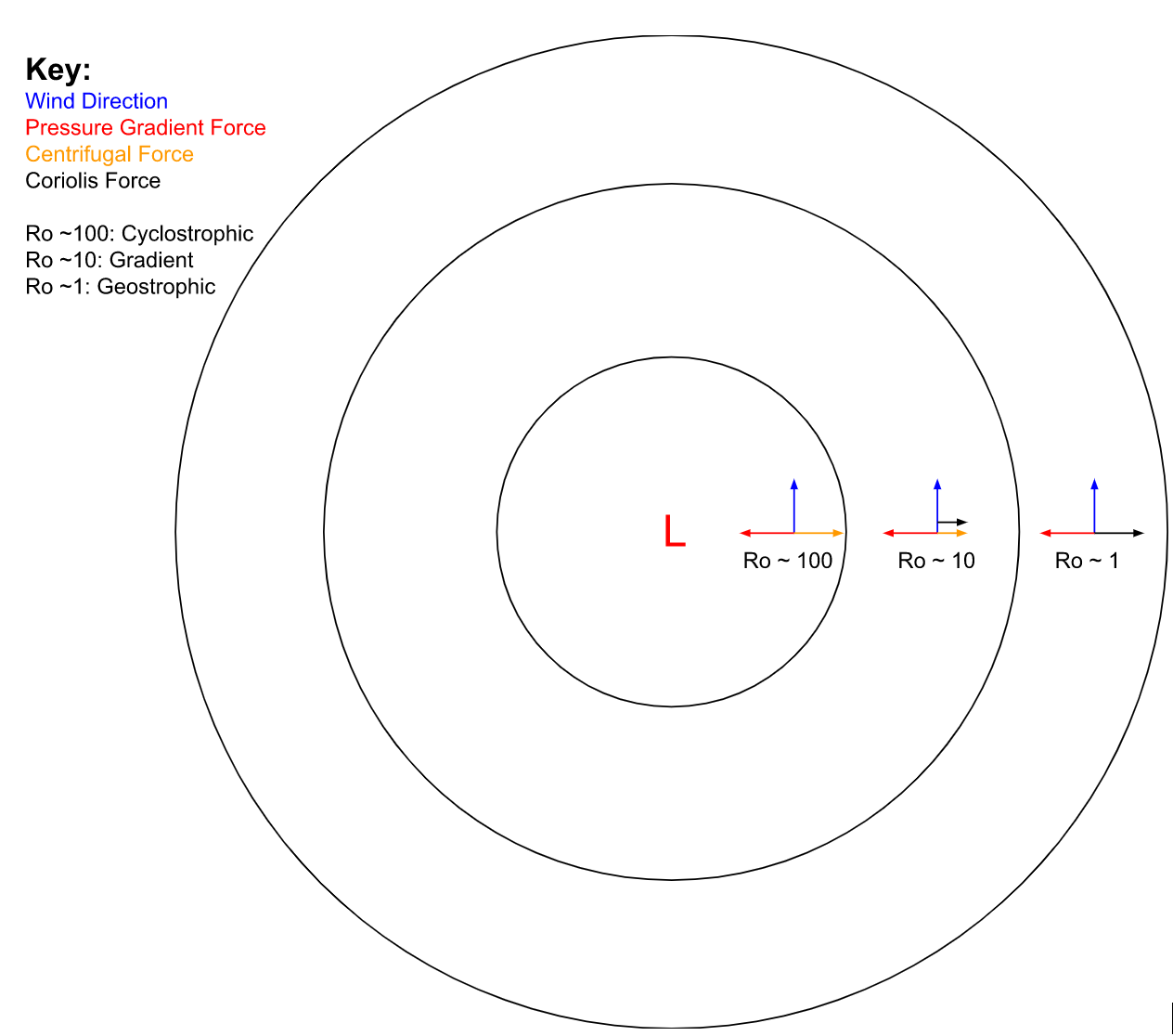 |
Rossby Number
The Rossby number (Ro), named for Carl-Gustav Arvid Rossby, is a dimensionless number used in describing fluid flow. The Rossby number is the ratio of inertial force to Coriolis force, terms , \mathbf \cdot \nabla \mathbf, \sim U^2 / L and \Omega \times \mathbf \sim U\Omega in the Navier–Stokes equations respectively. It is commonly used in geophysical phenomena in the oceans and atmosphere, where it characterizes the importance of Coriolis accelerations arising from planetary rotation. It is also known as the Kibel number. Definition and theory The Rossby number (Ro, not Ro) is defined as : \text = \frac, where ''U'' and ''L'' are respectively characteristic velocity and length scales of the phenomenon, and f = 2\Omega \sin \phi is the Coriolis frequency, with \Omega being the angular frequency of planetary rotation, and \phi the latitude. A small Rossby number signifies a system strongly affected by Coriolis forces, and a large Rossby number signifies a system in which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Latitude
In geography, latitude is a geographic coordinate system, geographic coordinate that specifies the north-south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at the south pole to 90° at the north pole, with 0° at the Equator. Parallel (latitude), Lines of constant latitude, or ''parallels'', run east-west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth. On its own, the term "latitude" normally refers to the ''geodetic latitude'' as defined below. Briefly, the geodetic latitude of a point is the angle formed between the vector perpendicular (or ''Normal (geometry), normal'') to the ellipsoidal surface from the point, and the equatorial plane, plane of the equator. Background Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Coriolis Effect
In physics, the Coriolis force is a pseudo force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise (or counterclockwise) rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term ''Coriolis force'' began to be used in connection with meteorology. Newton's laws of motion describe the motion of an object in an inertial (non-accelerating) frame of reference. When Newton's laws are transformed to a rotating frame of reference, the Coriolis and centrifugal accelerations appear. When applied ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Oscillation
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms. Oscillations occur not only in mechanical systems but also in dynamic systems in virtually every area of science: for example the beating of the human heart (for circulation), business cycles in economics, predator–prey population cycles in ecology, geothermal geysers in geology, vibration of strings in guitar and other string instruments, periodic firing of nerve cells in the brain, and the periodic swelling of Cepheid variable stars in astronomy. The term ''vibration'' is precisely used to describe a mechanical oscillation. Oscillation, especially rapid oscillation, may be an undesirable phenomenon in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |