|
Conditional Convergence
In mathematics, a series or integral is said to be conditionally convergent if it converges, but it does not converge absolutely. Definition More precisely, a series of real numbers \sum_^\infty a_n is said to converge conditionally if \lim_\,\sum_^m a_n exists (as a finite real number, i.e. not \infty or -\infty), but \sum_^\infty \left, a_n\ = \infty. A classic example is the alternating harmonic series given by 1 - + - + - \cdots =\sum\limits_^\infty , which converges to \ln (2), but is not absolutely convergent (see Harmonic series). Bernhard Riemann Georg Friedrich Bernhard Riemann (; ; 17September 182620July 1866) was a German mathematician who made profound contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the f ... proved that a conditionally convergent series may be rearranged to converge to any value at all, including ∞ or −∞; see Riemann series theorem. Agnew' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series (mathematics)
In mathematics, a series is, roughly speaking, an addition of Infinity, infinitely many Addition#Terms, terms, one after the other. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures in combinatorics through generating functions. The mathematical properties of infinite series make them widely applicable in other quantitative disciplines such as physics, computer science, statistics and finance. Among the Ancient Greece, Ancient Greeks, the idea that a potential infinity, potentially infinite summation could produce a finite result was considered paradoxical, most famously in Zeno's paradoxes. Nonetheless, infinite series were applied practically by Ancient Greek mathematicians including Archimedes, for instance in the Quadrature of the Parabola, quadrature of the parabola. The mathematical side of Zeno's paradoxes was resolved using the concept of a limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Convergence
In mathematics, an infinite series of numbers is said to converge absolutely (or to be absolutely convergent) if the sum of the absolute values of the summands is finite. More precisely, a real or complex series \textstyle\sum_^\infty a_n is said to converge absolutely if \textstyle\sum_^\infty \left, a_n\ = L for some real number \textstyle L. Similarly, an improper integral of a function, \textstyle\int_0^\infty f(x)\,dx, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if \textstyle\int_0^\infty , f(x), dx = L. A convergent series that is not absolutely convergent is called conditionally convergent. Absolute convergence is important for the study of infinite series, because its definition guarantees that a series will have some "nice" behaviors of finite sums that not all convergent series possess. For instance, rearrangements do not change the value of the sum, which is not necessarily true for conditionally converge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Series
In mathematics, an alternating series is an infinite series of terms that alternate between positive and negative signs. In capital-sigma notation this is expressed \sum_^\infty (-1)^n a_n or \sum_^\infty (-1)^ a_n with for all . Like any series, an alternating series is a convergent series if and only if the sequence of partial sums of the series converges to a limit. The alternating series test guarantees that an alternating series is convergent if the terms converge to 0 monotonically, but this condition is not necessary for convergence. Examples The geometric series − + − + ⋯ sums to . The alternating harmonic series has a finite sum but the harmonic series does not. The series 1-\frac+\frac-\ldots=\sum_^\infty\frac converges to \frac, but is not absolutely convergent. The Mercator series provides an analytic power series expression of the natural logarithm, given by \sum_^\infty \frac x^n = \ln (1+x),\;\;\;, x, \le1, x\ne-1. The functions si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Series (mathematics)
In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions: \sum_^\infty\frac = 1 + \frac + \frac + \frac + \frac + \cdots. The first n terms of the series sum to approximately \ln n + \gamma, where \ln is the natural logarithm and \gamma\approx0.577 is the Euler–Mascheroni constant. Because the logarithm has arbitrarily large values, the harmonic series does not have a finite limit: it is a divergent series. Its divergence was proven in the 14th century by Nicole Oresme using a precursor to the Cauchy condensation test for the convergence of infinite series. It can also be proven to diverge by comparing the sum to an integral, according to the integral test for convergence. Applications of the harmonic series and its partial sums include Divergence of the sum of the reciprocals of the primes, Euler's proof that there are infinitely many prime numbers, the analysis of the coupon collector's problem on how many random trials are nee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernhard Riemann
Georg Friedrich Bernhard Riemann (; ; 17September 182620July 1866) was a German mathematician who made profound contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as a foundational paper of analytic number theory. Through his pioneering contributions to differential geometry, Riemann laid the foundations of the mathematics of general relativity. He is considered by many to be one of the greatest mathematicians of all time. Early years Riemann was born on 17 September 1826 in Breselenz, a village near Danne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutation
In mathematics, a permutation of a set can mean one of two different things: * an arrangement of its members in a sequence or linear order, or * the act or process of changing the linear order of an ordered set. An example of the first meaning is the six permutations (orderings) of the set : written as tuples, they are (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). Anagrams of a word whose letters are all different are also permutations: the letters are already ordered in the original word, and the anagram reorders them. The study of permutations of finite sets is an important topic in combinatorics and group theory. Permutations are used in almost every branch of mathematics and in many other fields of science. In computer science, they are used for analyzing sorting algorithms; in quantum physics, for describing states of particles; and in biology, for describing RNA sequences. The number of permutations of distinct objects is factorial, us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Series Theorem
In mathematics, the Riemann series theorem, also called the Riemann rearrangement theorem, named after 19th-century German mathematician Bernhard Riemann, says that if an infinite series of real numbers is conditionally convergent, then its terms can be arranged in a permutation so that the new series converges to an arbitrary real number, and rearranged such that the new series diverges. This implies that a series of real numbers is absolutely convergent if and only if it is unconditionally convergent. As an example, the series : 1-1+\frac-\frac+\frac-\frac+\frac-\frac+\dots converges to 0 (for a sufficiently large number of terms, the partial sum gets arbitrarily near to 0); but replacing all terms with their absolute values gives : 1 + 1 + \frac + \frac + \frac + \frac + \dots which sums to infinity. Thus, the original series is conditionally convergent, and can be rearranged (by taking the first two positive terms followed by the first negative term, followed by the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Agnew's Theorem
Agnew's theorem, proposed by American mathematician Ralph Palmer Agnew, characterizes reorderings of terms of infinite series that preserve convergence for all series. Statement We call a permutation In mathematics, a permutation of a set can mean one of two different things: * an arrangement of its members in a sequence or linear order, or * the act or process of changing the linear order of an ordered set. An example of the first mean ... p: \mathbb \to \mathbb an ''Agnew permutation'' if there exists K \in \mathbb such that any interval that starts with 1 is mapped by to a union of at most intervals, i.e., \exists K \in \mathbb \, : \; \forall n \in \mathbb \;\; \#_(p( ,\,n) \le K\,, where \#_ counts the number of intervals. Agnew's theorem. p is an Agnew permutation \iff for all converging series of real or complex terms \sum_^\infty a_i\,, the series \sum_^\infty a_ converges to the same sum. Corollary 1. p^ (the inverse of p) is an Agnew permutati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lévy–Steinitz Theorem
In mathematics, the Lévy–Steinitz theorem identifies the set of values to which sums of rearrangements of an infinite series of vectors in R''n'' can converge. It was proved by Paul Lévy in his first published paper when he was 19 years old. In 1913 Ernst Steinitz filled in a gap in Lévy's proof and also proved the result by a different method. In an expository article, Peter Rosenthal stated the theorem in the following way.. : The set of all sums of rearrangements of a given series of vectors in a finite-dimensional real Euclidean space is either the empty set or a translate of a linear subspace (i.e., a set of the form ''v'' + ''M'', where ''v'' is a given vector and ''M'' is a linear subspace). See also *Riemann series theorem In mathematics, the Riemann series theorem, also called the Riemann rearrangement theorem, named after 19th-century German mathematician Bernhard Riemann, says that if an infinite series of real numbers is conditionally convergent, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
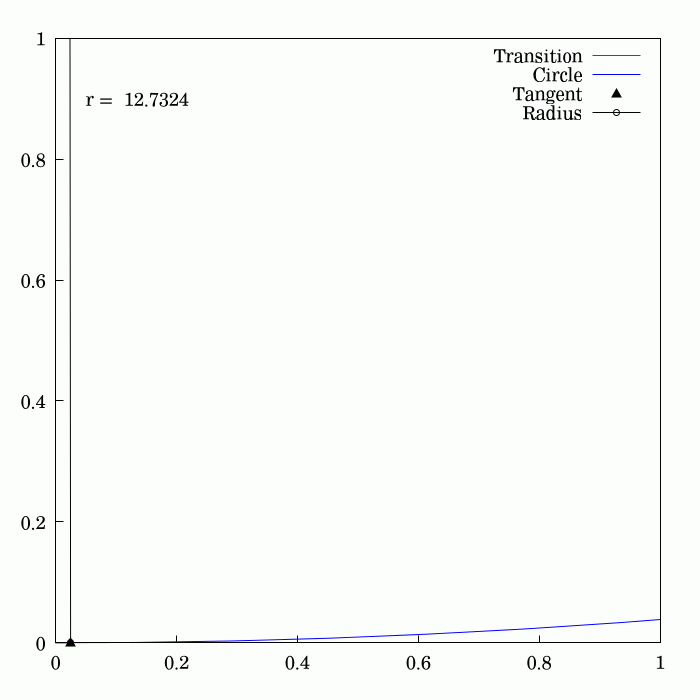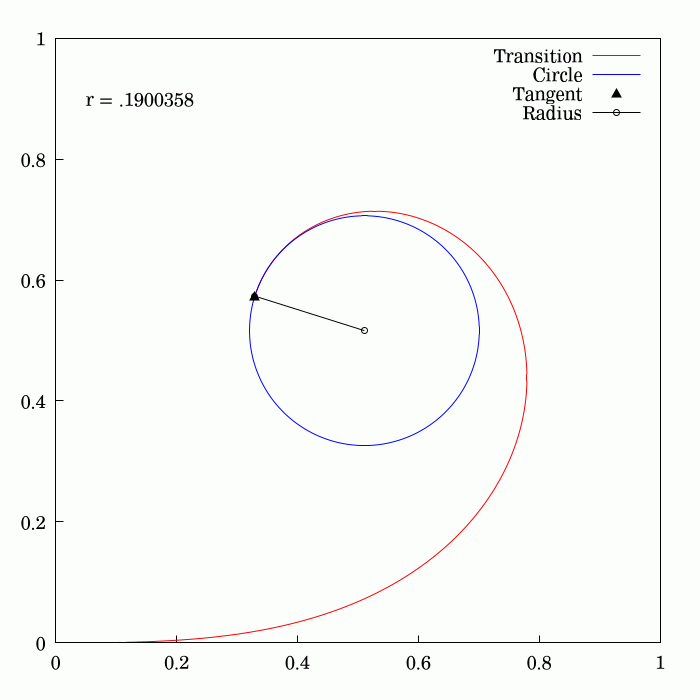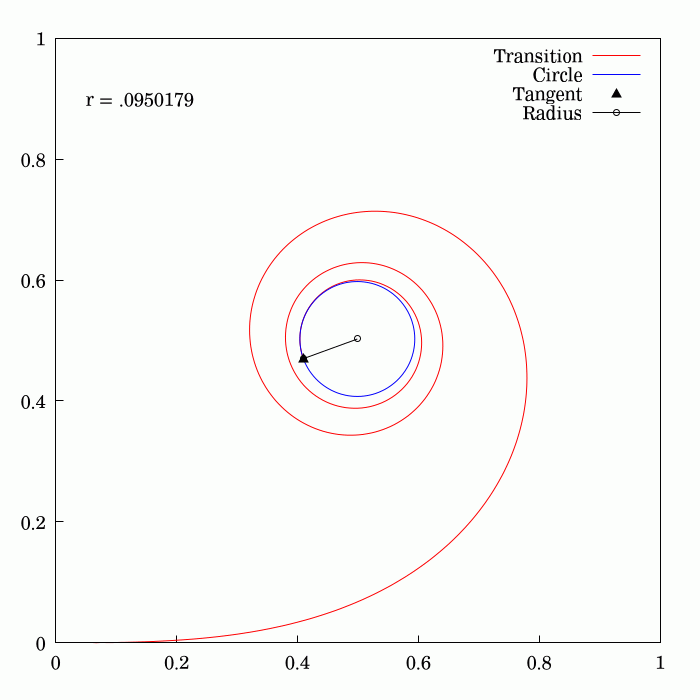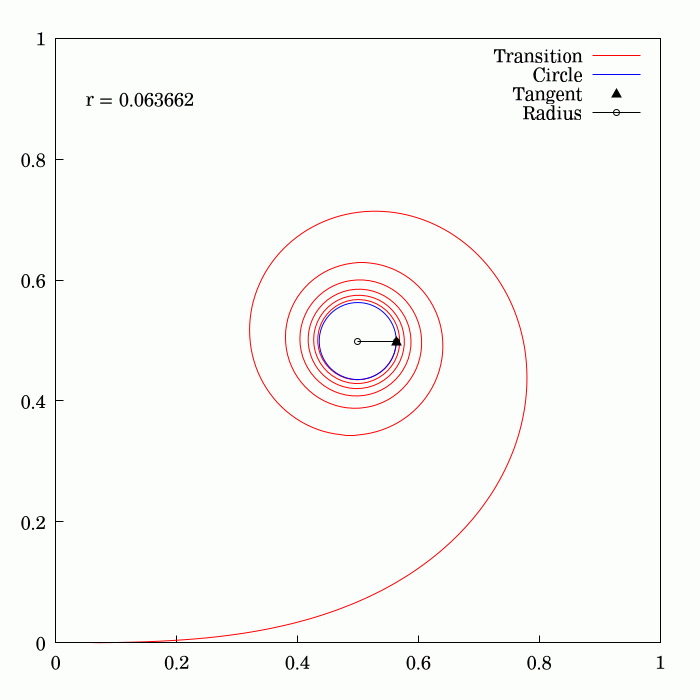
Fresnel Integral
250px, Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below). The Fresnel integrals and are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (). They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations: S(x) = \int_0^x \sin\left(t^2\right)\,dt, \quad C(x) = \int_0^x \cos\left(t^2\right)\,dt. The parametric curve is the Euler spiral or clothoid, a curve whose curvature varies linearly with arclength. The term Fresnel integral may also refer to the complex definite integral \int_^\infty e^ dx = \sqrte^ where is real and positive; this can be evaluated by closing a contour in the complex plane and applying Cauchy's integral theorem. Definition 250px, Fresnel integrals with arguments in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |