|
Arithmetic Derivative
In number theory, the Lagarias arithmetic derivative or number derivative is a function defined for integers, based on prime factorization, by analogy with the product rule for the derivative of a function that is used in mathematical analysis. There are many versions of "arithmetic derivatives", including the one discussed in this article (the Lagarias arithmetic derivative), such as Ihara's arithmetic derivative and Buium's arithmetic derivatives. Early history The arithmetic derivative was introduced by Spanish mathematician Josè Mingot Shelly in 1911. The arithmetic derivative also appeared in the 1950 Putnam Competition. Definition For natural numbers , the arithmetic derivative In this article we use Oliver Heaviside's notation for the arithmetic derivative of . There are various other notations possible, such as ; a full discussion is available here for general differential operators, of which the arithmetic derivative can be considered one. Heaviside's notation is used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Number Theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example, rational numbers), or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory can often be understood through the study of Complex analysis, analytical objects, such as the Riemann zeta function, that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, as for instance how irrational numbers can be approximated by fractions (Diophantine approximation). Number theory is one of the oldest branches of mathematics alongside geometry. One quirk of number theory is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example, The set of all rational numbers is often referred to as "the rationals", and is closed under addition, subtraction, multiplication, and division by a nonzero rational number. It is a field under these operations and therefore also called the field of rationals or the field of rational numbers. It is usually denoted by boldface , or blackboard bold A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Univariate
In mathematics, a univariate object is an expression (mathematics), expression, equation, function (mathematics), function or polynomial involving only one Variable (mathematics), variable. Objects involving more than one variable are ''wikt:multivariate, multivariate''. In some cases the distinction between the univariate and multivariate cases is fundamental; for example, the fundamental theorem of algebra and Euclid's algorithm for polynomials are fundamental properties of univariate polynomials that cannot be generalized to multivariate polynomials. In statistics, a univariate Frequency distribution, distribution characterizes one variable, although it can be applied in other ways as well. For example, univariate data are composed of a single scalar (mathematics), scalar component. In time series analysis, the whole time series is the "variable": a univariate time series is the series of values over time of a single quantity. Correspondingly, a "multivariate time series" charac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Derivation (differential Algebra)
In mathematics, a derivation is a function on an algebra that generalizes certain features of the derivative operator. Specifically, given an algebra ''A'' over a ring or a field ''K'', a ''K''-derivation is a ''K''-linear map that satisfies Leibniz's law: : D(ab) = a D(b) + D(a) b. More generally, if ''M'' is an ''A''-bimodule, a ''K''-linear map that satisfies the Leibniz law is also called a derivation. The collection of all ''K''-derivations of ''A'' to itself is denoted by Der''K''(''A''). The collection of ''K''-derivations of ''A'' into an ''A''-module ''M'' is denoted by . Derivations occur in many different contexts in diverse areas of mathematics. The partial derivative with respect to a variable is an R-derivation on the algebra of real-valued differentiable functions on R''n''. The Lie derivative with respect to a vector field is an R-derivation on the algebra of differentiable functions on a differentiable manifold; more generally it is a derivation on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Polynomial Ring
In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates (traditionally also called variables) with coefficients in another ring, often a field. Often, the term "polynomial ring" refers implicitly to the special case of a polynomial ring in one indeterminate over a field. The importance of such polynomial rings relies on the high number of properties that they have in common with the ring of the integers. Polynomial rings occur and are often fundamental in many parts of mathematics such as number theory, commutative algebra, and algebraic geometry. In ring theory, many classes of rings, such as unique factorization domains, regular rings, group rings, rings of formal power series, Ore polynomials, graded rings, have been introduced for generalizing some properties of polynomial rings. A closely related notion is that of the ring of polynomial functions on a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Field Of Fractions
In abstract algebra, the field of fractions of an integral domain is the smallest field in which it can be embedded. The construction of the field of fractions is modeled on the relationship between the integral domain of integers and the field of rational numbers. Intuitively, it consists of ratios between integral domain elements. The field of fractions of an integral domain R is sometimes denoted by \operatorname(R) or \operatorname(R), and the construction is sometimes also called the fraction field, field of quotients, or quotient field of R. All four are in common usage, but are not to be confused with the quotient of a ring by an ideal, which is a quite different concept. For a commutative ring that is not an integral domain, the analogous construction is called the localization or ring of quotients. Definition Given an integral domain R and letting R^* = R \setminus \, we define an equivalence relation on R \times R^* by letting (n,d) \sim (m,b) whenever nb = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
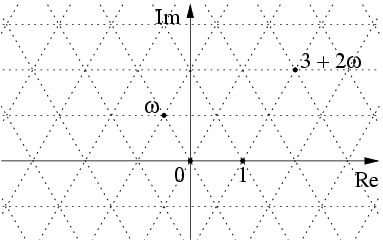 |
Eisenstein Integer
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form : z = a + b\omega , where and are integers and : \omega = \frac = e^ is a Root of unity#General definition, primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a Countable set, countably infinite set. Properties The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field – the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial : z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~. In particular, satisfies the equation : \omega^2 + \omega + 1 = 0~. The product of two Eisenstein integers and i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Gaussian Integer
In number theory, a Gaussian integer is a complex number whose real and imaginary parts are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as \mathbf[i] or \Z[i]. Gaussian integers share many properties with integers: they form a Euclidean domain, and thus have a Euclidean division and a Euclidean algorithm; this implies unique factorization and many related properties. However, Gaussian integers do not have a total order that respects arithmetic. Gaussian integers are algebraic integers and form the simplest ring of quadratic integers. Gaussian integers are named after the German mathematician Carl Friedrich Gauss. Basic definitions The Gaussian integers are the set :\mathbf[i]=\, \qquad \text i^2 = -1. In other words, a Gaussian integer is a complex number such that its real part, real and imaginary parts are both integers. Since the Gaussian integers are closed under addition a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Unique Factorization Domain
In mathematics, a unique factorization domain (UFD) (also sometimes called a factorial ring following the terminology of Bourbaki) is a ring in which a statement analogous to the fundamental theorem of arithmetic holds. Specifically, a UFD is an integral domain (a nontrivial commutative ring in which the product of any two non-zero elements is non-zero) in which every non-zero non- unit element can be written as a product of irreducible elements, uniquely up to order and units. Important examples of UFDs are the integers and polynomial rings in one or more variables with coefficients coming from the integers or from a field. Unique factorization domains appear in the following chain of class inclusions: Definition Formally, a unique factorization domain is defined to be an integral domain ''R'' in which every non-zero element ''x'' of ''R'' which is not a unit can be written as a finite product of irreducible elements ''p''''i'' of ''R'': : ''x'' = ''p''1 ''p''2 � ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Irrational Number
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the case of irrational numbers, the decimal expansion does not terminate, nor end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Bo Åhlander
Bo or BO may refer to Arts and entertainment *Box office, where tickets to an event are sold, and by extension, the amount of business a production receives *'' BA:BO'', 2008 South Korean film * ''Bo'' (film), a Belgian film starring Ella-June Henrard and directed by Hans Herbots * Bo (instrument), a Chinese cymbal * Bo, a Greek rapper *'' Bō: Path of the Teal Lotus'', a platform game *'' Call of Duty: Black Ops'', a first-person shooter video game *'' Blood Omen: Legacy of Kain'', first in the ''Legacy of Kain'' video game series People * Bo (given name), name origin, plus a list of people and fictional characters with the name or nickname * Bo (surname), name origin, plus a list of people with the surname ** Bo (Chinese surname), Chinese family names ** Bő (genus), Hungarian medieval noble clan * Bø (other), which includes several people with the surname *Bo people (China), a nearly extinct minority population in Southern China *Bo people of Laos, see List of eth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |