|
Zeroth-order Approximation
In science, engineering, and other quantitative disciplines, order of approximation refers to formal or informal expressions for how accurate an approximation is. Usage in science and engineering In formal expressions, the ordinal number used before the word order refers to the highest power in the series expansion used in the approximation. The expressions: a ''zeroth-order approximation'', a ''first-order approximation'', a ''second-order approximation'', and so forth are used as fixed phrases. The expression a ''zero-order approximation'' is also common. Cardinal numerals are occasionally used in expressions like an ''order-zero approximation'', an ''order-one approximation'', etc. The omission of the word ''order'' leads to phrases that have less formal meaning. Phrases like first approximation or to a first approximation may refer to ''a roughly approximate value of a quantity''. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
English Numerals
English number words include numerals and various words derived from them, as well as a large number of words borrowed from other languages. Cardinal numbers Cardinal numbers refer to the size of a group. In English, these words are numerals. If a number is in the range 21 to 99, and the second digit is not zero, the number is typically written as two words separated by a hyphen. In English, the hundreds are perfectly regular, except that the word ''hundred'' remains in its singular form regardless of the number preceding it. So too are the thousands, with the number of thousands followed by the word "thousand". The number one thousand may be written 1 000 or 1000 or 1,000; larger numbers are written for example 10 000 or 10,000 for ease of reading. European languages that use the comma as a decimal separator may correspondingly use the period as a thousands separator. As a result, some style guides recommend avoidance of the comma (,) as either separator and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
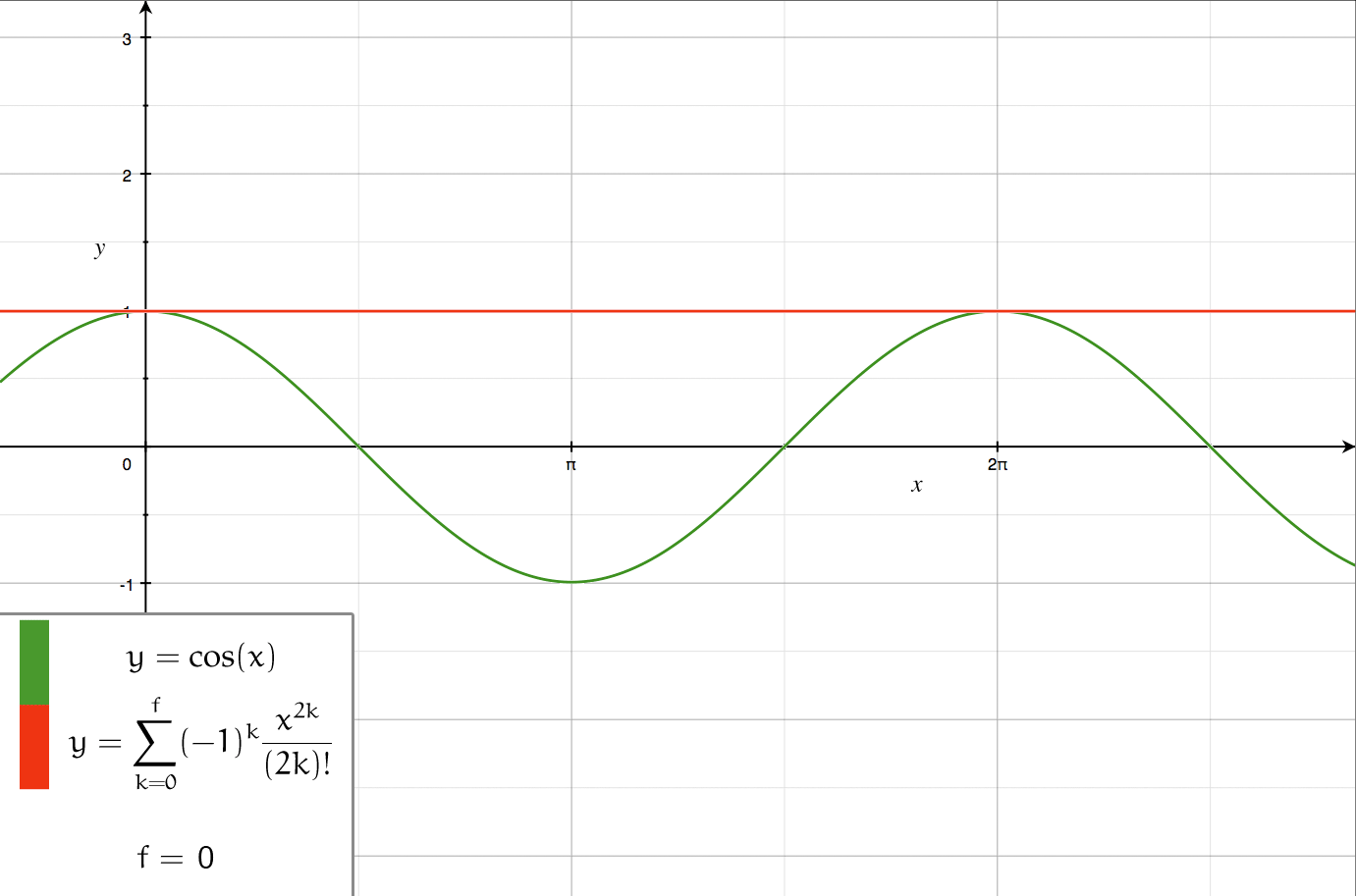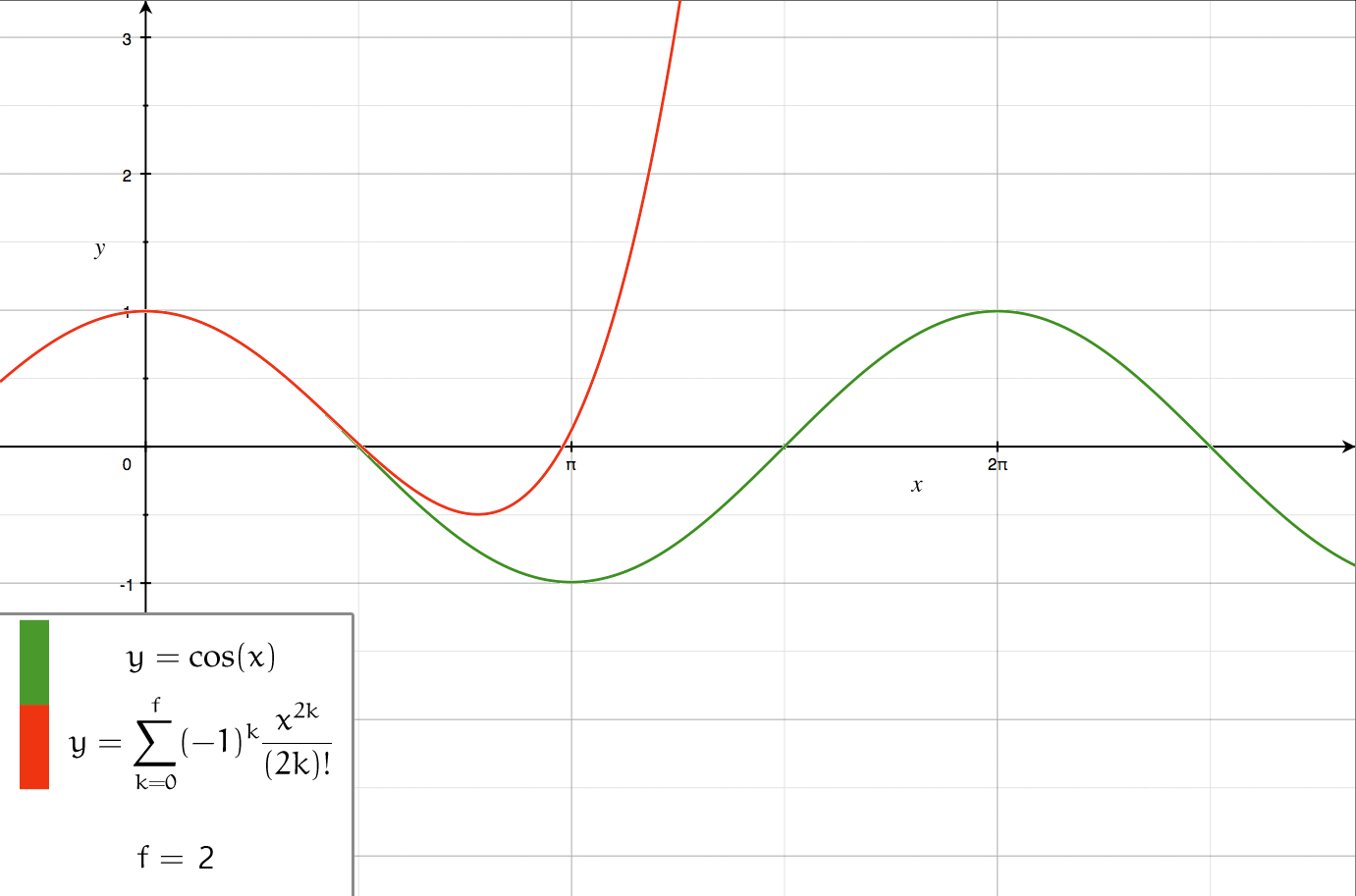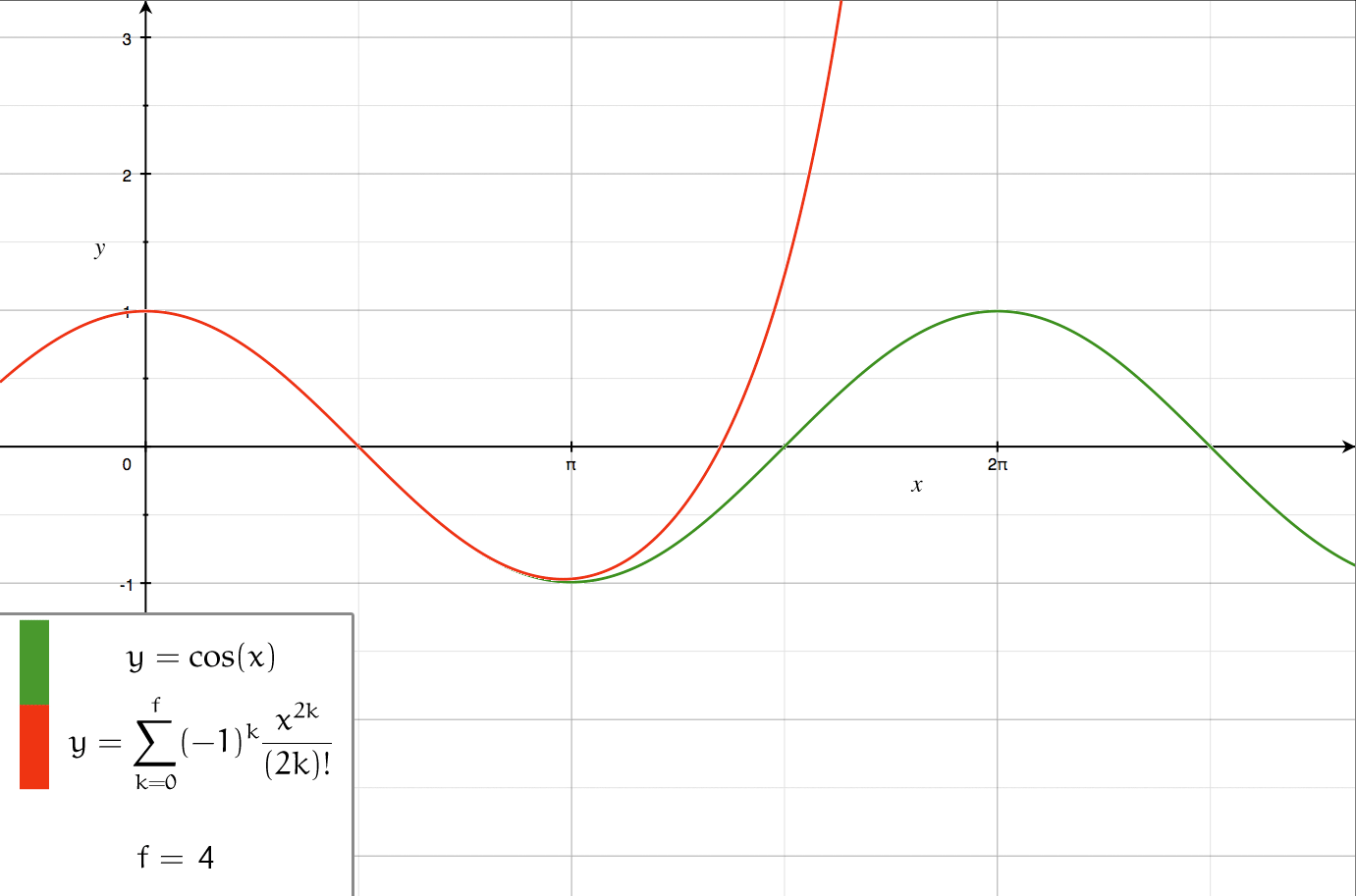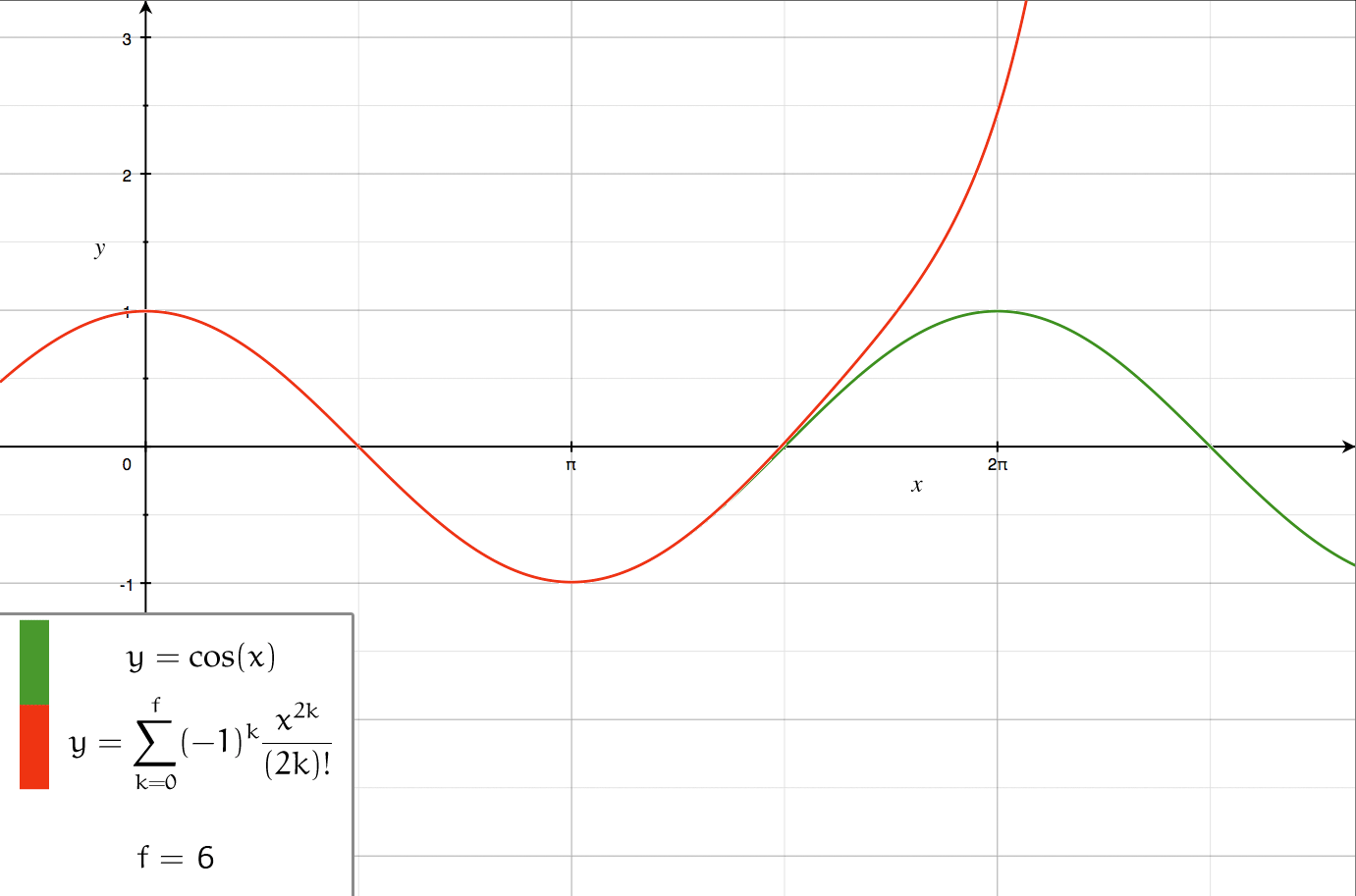
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scientist
A scientist is a person who Scientific method, researches to advance knowledge in an Branches of science, area of the natural sciences. In classical antiquity, there was no real ancient analog of a modern scientist. Instead, philosophers engaged in the philosophical study of nature called natural philosophy, a precursor of natural science. Though Thales ( 624–545 BC) was arguably the first scientist for describing how cosmic events may be seen as natural, not necessarily caused by gods,Frank N. Magill''The Ancient World: Dictionary of World Biography'', Volume 1 Routledge, 2003 it was not until the 19th century in science, 19th century that the term ''scientist'' came into regular use after it was coined by the theologian, philosopher, and historian of science William Whewell in 1833. History The roles of "scientists", and their predecessors before the emergence of modern scientific disciplines, have evolved considerably over time. Scientists of different er ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor's Theorem
In calculus, Taylor's theorem gives an approximation of a k-times differentiable function around a given point by a polynomial of degree k, called the k-th-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order ''k'' of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial. Taylor's theorem is named after the mathematician Brook Taylor, who stated a version of it in 1715, although an earlier version of the result was already mentioned in 1671 in science, 1671 by James Gregory (astronomer and mathematician), James Gregory. Taylor's theorem is taught in introductory-level calculus courses and is one of the central elementary tools in mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Significant Figures
Significant figures, also referred to as significant digits, are specific digits within a number that is written in positional notation that carry both reliability and necessity in conveying a particular quantity. When presenting the outcome of a measurement (such as length, pressure, volume, or mass), if the number of digits exceeds what the measurement instrument can resolve, only the digits that are determined by the resolution are dependable and therefore considered significant. For instance, if a length measurement yields 114.8 mm, using a ruler with the smallest interval between marks at 1 mm, the first three digits (1, 1, and 4, representing 114 mm) are certain and constitute significant figures. Further, digits that are uncertain yet meaningful are also included in the significant figures. In this example, the last digit (8, contributing 0.8 mm) is likewise considered significant despite its uncertainty. Therefore, this measurement contains ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percent Error
In any quantitative science, the terms relative change and relative difference are used to compare two quantities while taking into account the "sizes" of the things being compared, i.e. dividing by a ''standard'' or ''reference'' or ''starting'' value. The comparison is expressed as a ratio and is a unitless number. By multiplying these ratios by 100 they can be expressed as percentages so the terms percentage change, percent(age) difference, or relative percentage difference are also commonly used. The terms "change" and "difference" are used interchangeably. Relative change is often used as a quantitative indicator of quality assurance and quality control for repeated measurements where the outcomes are expected to be the same. A special case of percent change (relative change expressed as a percentage) called '' percent error'' occurs in measuring situations where the reference value is the accepted or actual value (perhaps theoretically determined) and the value being compa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Accuracy And Precision
Accuracy and precision are two measures of ''observational error''. ''Accuracy'' is how close a given set of measurements (observations or readings) are to their ''true value''. ''Precision'' is how close the measurements are to each other. The International Organization for Standardization (ISO) defines a related measure: ''trueness'', "the closeness of agreement between the arithmetic mean of a large number of test results and the true or accepted reference value." While ''precision'' is a description of ''random errors'' (a measure of statistical variability), ''accuracy'' has two different definitions: # More commonly, a description of ''systematic errors'' (a measure of statistical bias of a given measure of central tendency, such as the mean). In this definition of "accuracy", the concept is independent of "precision", so a particular set of data can be said to be accurate, precise, both, or neither. This concept corresponds to ISO's ''trueness''. # A combination of both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series Expansion
In mathematics, a series expansion is a technique that expresses a Function (mathematics), function as an infinite sum, or Series (mathematics), series, of simpler functions. It is a method for calculating a Function (mathematics), function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called ''Series (mathematics), series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. Taylor series A ''Taylor series'' is a power ser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series (mathematics)
In mathematics, a series is, roughly speaking, an addition of Infinity, infinitely many Addition#Terms, terms, one after the other. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures in combinatorics through generating functions. The mathematical properties of infinite series make them widely applicable in other quantitative disciplines such as physics, computer science, statistics and finance. Among the Ancient Greece, Ancient Greeks, the idea that a potential infinity, potentially infinite summation could produce a finite result was considered paradoxical, most famously in Zeno's paradoxes. Nonetheless, infinite series were applied practically by Ancient Greek mathematicians including Archimedes, for instance in the Quadrature of the Parabola, quadrature of the parabola. The mathematical side of Zeno's paradoxes was resolved using the concept of a limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |