|
Vladimir Bogachev
Vladimir Igorevich Bogachev (russian: Владимир Игоревич Богачёв; born in 1961) is an eminent Russian mathematician and Full Professor of the Department of Mechanics and Mathematics of the Lomonosov Moscow State University. He is an expert in measure theory, probability theory Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set o ..., infinite-dimensional analysis and partial differential equations arising in mathematical physics. His research was distinguished by several awards including the medal and the prize of the Academy of Sciences of the Soviet Union (1990); Award of the Japan Society for the Promotion of Science (2000); the Doob Lecture of the Bernoulli Society for Mathematical Statistics and Probability, Bernoulli Society (2017); and the Kolmogorov Prize of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematical model, models, and mathematics#Calculus and analysis, change. History One of the earliest known mathematicians were Thales of Miletus (c. 624–c.546 BC); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem. The number of known mathematicians grew when Pythagoras of Samos (c. 582–c. 507 BC) established the Pythagoreans, Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand ( yi, ישראל געלפֿאַנד, russian: Изра́иль Моисе́евич Гельфа́нд, uk, Ізраїль Мойсейович Гельфанд; – 5 October 2009) was a prominent Soviet-American mathematician. He made significant contributions to many branches of mathematics, including group theory, representation theory and functional analysis. The recipient of many awards, including the Order of Lenin and the first Wolf Prize, he was a Foreign Fellow of the Royal Society and professor at Moscow State University and, after immigrating to the United States shortly before his 76th birthday, at Rutgers University. Gelfand is also a 1994 MacArthur Fellow. His legacy continues through his students, who include Endre Szemerédi, Alexandre Kirillov, Edward Frenkel, Joseph Bernstein, David Kazhdan, as well as his own son, Sergei Gelfand. Early years A native of Kherson G ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
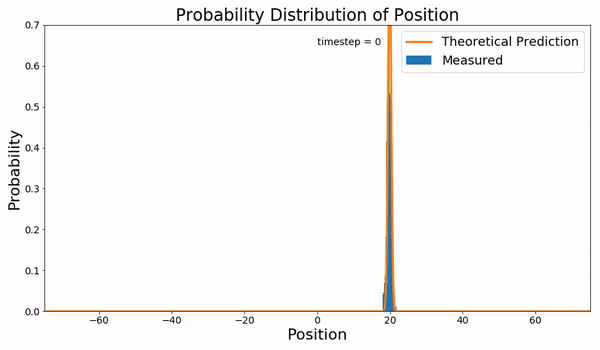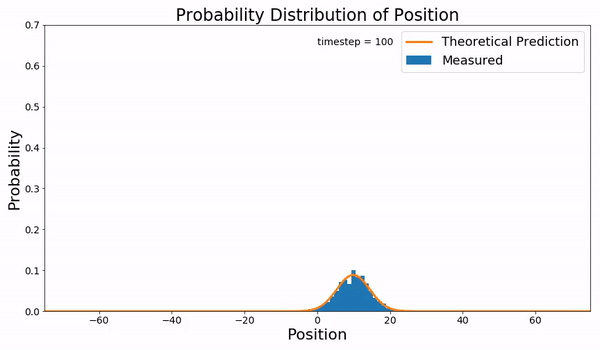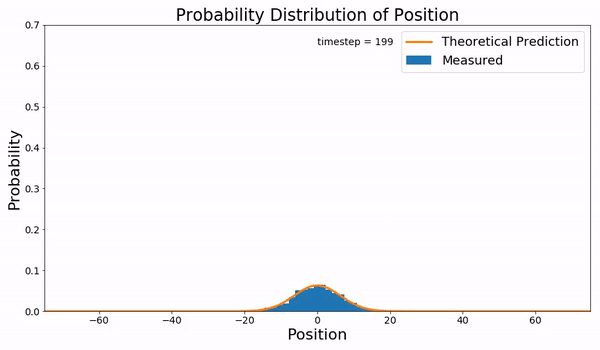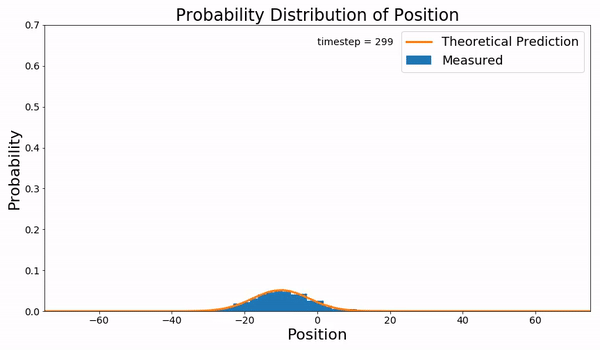
Fokker–Planck Equation
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comm
The command in the Unix family of computer operating systems is a utility that is used to compare two files for common and distinct lines. is specified in the POSIX standard. It has been widely available on Unix-like operating systems since the mid to late 1980s. History Written by Lee E. McMahon, first appeared in Version 4 Unix. The version of bundled in GNU coreutils was written by Richard Stallman and David MacKenzie. Usage reads two files as input, regarded as lines of text. outputs one file, which contains three columns. The first two columns contain lines unique to the first and second file, respectively. The last column contains lines common to both. This functionally is similar to . Columns are typically distinguished with the character. If the input files contain lines beginning with the separator character, the output columns can become ambiguous. For efficiency, standard implementations of expect both input files to be sequenced in the same line collati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Coefficient
Diffusivity, mass diffusivity or diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species (or the driving force for diffusion). Diffusivity is encountered in Fick's law and numerous other equations of physical chemistry. The diffusivity is generally prescribed for a given pair of species and pairwise for a multi-species system. The higher the diffusivity (of one substance with respect to another), the faster they diffuse into each other. Typically, a compound's diffusion coefficient is ~10,000× as great in air as in water. Carbon dioxide in air has a diffusion coefficient of 16 mm2/s, and in water its diffusion coefficient is 0.0016 mm2/s. Diffusivity has dimensions of length2 / time, or m2/s in SI units and cm2/s in CGS units. Temperature dependence of the diffusion coefficient Solids The diffusion coefficient in solids at different temperatures is generally found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions that are given on a hypersurface in the domain. A Cauchy problem can be an initial value problem or a boundary value problem (for this case see also Cauchy boundary condition). It is named after Augustin-Louis Cauchy. Formal statement For a partial differential equation defined on R''n+1'' and a smooth manifold ''S'' ⊂ R''n+1'' of dimension ''n'' (''S'' is called the Cauchy surface), the Cauchy problem consists of finding the unknown functions u_1,\dots,u_N of the differential equation with respect to the independent variables t,x_1,\dots,x_n that satisfiesPetrovskii, I. G. (1954). Lectures on partial differential equations. Interscience Publishers, Inc, Translated by A. Shenitzer, (Dover publications, 1991) \begin&\frac = F_i\left(t,x_1,\dots,x_n,u_1,\dots,u_N,\dots,\frac,\dots\right) \\ &\text i,j = 1,2,\dots,N;\, k_0+k_1+\dots+k_n=k\leq n_j;\, k_0 [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov ( rus, Андре́й Никола́евич Колмого́ров, p=ɐnˈdrʲej nʲɪkɐˈlajɪvʲɪtɕ kəlmɐˈɡorəf, a=Ru-Andrey Nikolaevich Kolmogorov.ogg, 25 April 1903 – 20 October 1987) was a Soviet mathematician who contributed to the mathematics of probability theory, topology, intuitionistic logic, turbulence, classical mechanics, algorithmic information theory and computational complexity. Biography Early life Andrey Kolmogorov was born in Tambov, about 500 kilometers south-southeast of Moscow, in 1903. His unmarried mother, Maria Y. Kolmogorova, died giving birth to him. Andrey was raised by two of his aunts in Tunoshna (near Yaroslavl) at the estate of his grandfather, a well-to-do nobleman. Little is known about Andrey's father. He was supposedly named Nikolai Matveevich Kataev and had been an agronomist. Kataev had been exiled from St. Petersburg to the Yaroslavl province after his participation in the revolutionary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Distribution
Stationary distribution may refer to: * A special distribution for a Markov chain such that if the chain starts with its stationary distribution, the marginal distribution of all states at any time will always be the stationary distribution. Assuming irreducibility, the stationary distribution is always unique if it exists, and its existence can be implied by positive recurrence of all states. The stationary distribution has the interpretation of the limiting distribution when the chain is irreducible and aperiodic. * The marginal distribution of a stationary process or stationary time series * The set of joint probability distributions of a stationary process or stationary time series In some fields of application, the term stable distribution is used for the equivalent of a stationary (marginal) distribution, although in probability and statistics the term has a rather different meaning: see stable distribution. Crudely stated, all of the above are specific cases of a common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sergio Albeverio
Sergio Albeverio (born 17 January 1939) is a Swiss mathematician and mathematical physicist working in numerous fields of mathematics and its applications. In particular he is known for his work in probability theory, analysis (including infinite dimensional, non-standard, and stochastic analysis), mathematical physics, and in the areas algebra, geometry, number theory, as well as in applications, from natural to social-economic sciences. He initiated (with Raphael Høegh-Krohn) a systematic mathematical theory of Feynman path integrals and of infinite dimensional Dirichlet forms and associated stochastic processes (with applications particularly in quantum mechanics, statistical mechanics and quantum field theory). He also gave essential contributions to the development of areas such as ''p''-adic functional and stochastic analysis as well as to the singular perturbation theory for differential operators. Other important contributions concern constructive quantum field the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant Measure
In mathematics, an invariant measure is a measure that is preserved by some function. The function may be a geometric transformation. For examples, circular angle is invariant under rotation, hyperbolic angle is invariant under squeeze mapping, and a difference of slopes is invariant under shear mapping. Ergodic theory is the study of invariant measures in dynamical systems. The Krylov–Bogolyubov theorem proves the existence of invariant measures under certain conditions on the function and space under consideration. Definition Let (X, \Sigma) be a measurable space and let f : X \to X be a measurable function from X to itself. A measure \mu on (X, \Sigma) is said to be invariant under f if, for every measurable set A in \Sigma, \mu\left(f^(A)\right) = \mu(A). In terms of the pushforward measure, this states that f_*(\mu) = \mu. The collection of measures (usually probability measures) on X that are invariant under f is sometimes denoted M_f(X). The collection of ergodic m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Continuity
In calculus, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship between the two central operations of calculus— differentiation and integration. This relationship is commonly characterized (by the fundamental theorem of calculus) in the framework of Riemann integration, but with absolute continuity it may be formulated in terms of Lebesgue integration. For real-valued functions on the real line, two interrelated notions appear: absolute continuity of functions and absolute continuity of measures. These two notions are generalized in different directions. The usual derivative of a function is related to the '' Radon–Nikodym derivative'', or ''density'', of a measure. We have the following chains of inclusions for functions over a compact subset of the real line: : '' absolutely continuous'' ⊆ '' uniformly continuous'' = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michael Röckner
Michael Röckner is a mathematician working in the fields of Stochastic analysis and Mathematical Physics. He obtained his PhD at the University of Bielefeld in 1984 under the supervision of Sergio Albeverio Sergio Albeverio (born 17 January 1939) is a Swiss mathematician and mathematical physicist working in numerous fields of mathematics and its applications. In particular he is known for his work in probability theory, analysis (including infini ... and Christopher John Preston. Together with Claudia Prévôt, he wrote the book ''A Concise Course on Stochastic Partial Differential Equations''. * References Living people 20th-century German mathematicians Probability theorists Year of birth missing (living people) 21st-century German mathematicians Sir Edmund Whittaker Memorial Prize winners Presidents of the German Mathematical Society {{Germany-mathematician-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |