|
Virial Expansion
The virial expansion is a model of thermodynamic equations of state. It expresses the pressure of a gas in local Thermodynamic equilibrium, equilibrium as a power series of the density. This equation may be represented in terms of the compressibility factor, , as Z \equiv \frac = A + B\rho + C\rho^2 + \cdots This equation was first proposed by Heike Kamerlingh Onnes, Kamerlingh Onnes.Kamerlingh Onnes, H."Expression of the equation of state of gases and liquids by means of series" ''KNAW, Proceedings'', 4, 1901-1902, Amsterdam, 125-147 (1902). The terms , , and represent the virial coefficients. The leading coefficient is defined as the constant value of 1, which ensures that the equation reduces to the ideal gas expression as the gas density approaches zero. Second and third virial coefficients The second, , and third, , virial coefficients have been studied extensively and tabulated for many fluids for more than a century. Two of the most extensive compilations are in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equations Of State
In physics and chemistry, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Though there are many equations of state, none accurately predicts properties of substances under all conditions. The quest for a universal equation of state has spanned three centuries. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Van Der Waals Equation
The van der Waals equation is a mathematical formula that describes the behavior of real gases. It is an equation of state that relates the pressure, volume, Avogadro's law, number of molecules, and temperature in a fluid. The equation modifies the ideal gas law in two ways: first, it considers particles to have a finite diameter (whereas an ideal gas consists of point particles); second, its particles interact with each other (unlike an ideal gas, whose particles move as though alone in the volume). The equation is named after Dutch physicist Johannes Diderik van der Waals, who first derived it in 1873 as part of his doctoral thesis. Van der Waals based the equation on the idea that fluids are composed of discrete particles, which few scientists believed existed. However, the equation accurately predicted the behavior of a fluid around its Critical point (thermodynamics), critical point, which had been discovered a few years earlier. Its qualitative and quantitative agreement w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ..., information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virial Theorem
In mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by a conservative force (where the work done is independent of path), with that of the total potential energy of the system. Mathematically, the theorem states that \langle T \rangle = -\frac12\,\sum_^N \langle\mathbf_k \cdot \mathbf_k\rangle, where T is the total kinetic energy of the N particles, F_k represents the force on the kth particle, which is located at position , and angle brackets represent the average over time of the enclosed quantity. The word virial for the right-hand side of the equation derives from , the Latin word for "force" or "energy", and was given its technical definition by Rudolf Clausius in 1870. The significance of the virial theorem is that it allows the average total kinetic energy to be calculated even for very complicated systems that defy an exact solution, such as those co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and Thermodynamic temperature, temperature respectively; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory of gases, kinetic theory, as was achieved (independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state function, state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triple Point
In thermodynamics, the triple point of a substance is the temperature and pressure at which the three Phase (matter), phases (gas, liquid, and solid) of that substance coexist in thermodynamic equilibrium.. It is that temperature and pressure at which the sublimation (phase transition), sublimation, Melting, fusion, and vaporisation curves meet. For example, the triple point of Mercury (element), mercury occurs at a temperature of and a pressure of 0.165 Milli, mPascal (unit), Pa. In addition to the triple point for solid, liquid, and gas phases, a triple point may involve more than one solid phase, for substances with multiple polymorphism (materials science), polymorphs. Helium-4 is unusual in that it has no sublimation/deposition curve and therefore no triple points where its solid phase meets its gas phase. Instead, it has a vapor-liquid-superfluid point, a solid-liquid-superfluid point, a solid-solid-liquid point, and a solid-solid-superfluid point. None of these should be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molar Volume
In chemistry and related fields, the molar volume, symbol ''V''m, or \tilde V of a substance is the ratio of the volume (''V'') occupied by a substance to the amount of substance (''n''), usually at a given temperature and pressure. It is also equal to the molar mass (''M'') divided by the mass density (''ρ''): V_ = \frac = \frac The molar volume has the SI unit of cubic metres per mole (m3/mol), although it is more typical to use the units cubic decimetres per mole (dm3/mol) for gases, and cubic centimetres per mole (cm3/mol) for liquids and solids. Definition The molar volume of a substance ''i'' is defined as its molar mass divided by its density ''ρ''''i''0: V_ = For an ideal mixture containing ''N'' components, the molar volume of the mixture is the weighted sum of the molar volumes of its individual components. For a real mixture the molar volume cannot be calculated without knowing the density: V_ = \frac There are many liquid–liquid mixtures, for instance mix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
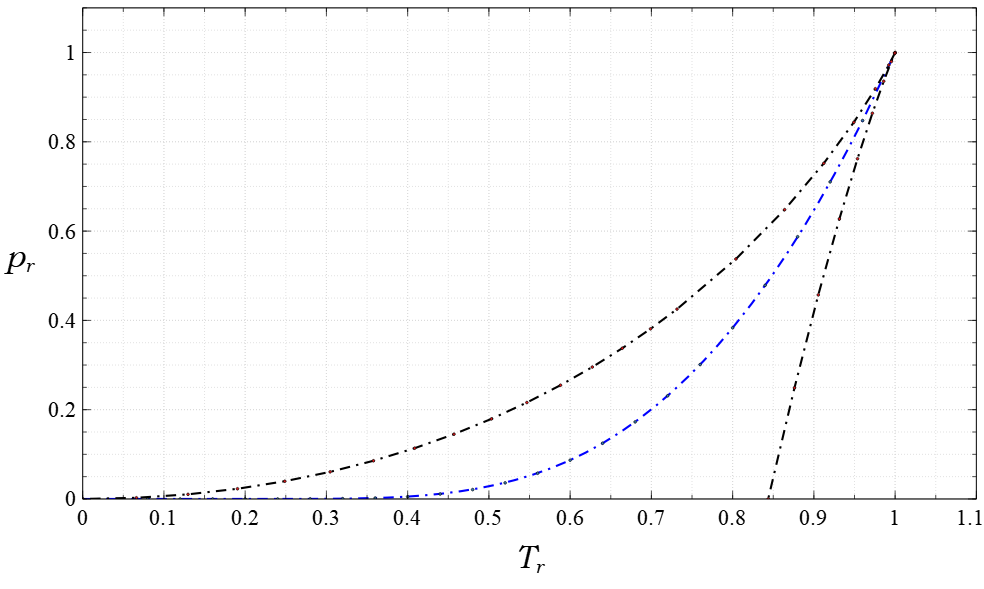
Argon B C
Argon is a chemical element; it has symbol Ar and atomic number 18. It is in group 18 of the periodic table and is a noble gas. Argon is the third most abundant gas in Earth's atmosphere, at 0.934% (9340 ppmv). It is more than twice as abundant as water vapor (which averages about 4000 ppmv, but varies greatly), 23 times as abundant as carbon dioxide (400 ppmv), and more than 500 times as abundant as neon (18 ppmv). Argon is the most abundant noble gas in Earth's crust, comprising 0.00015% of the crust. Nearly all argon in Earth's atmosphere is radiogenic argon-40, derived from the decay of potassium-40 in Earth's crust. In the universe, argon-36 is by far the most common argon isotope, as it is the most easily produced by stellar nucleosynthesis in supernovas. The name "argon" is derived from the Greek word , neuter singular form of meaning 'lazy' or 'inactive', as a reference to the fact that the element undergoes almost no chemical reactions. The complete octet (eight ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and even by industry. Further, both spellings are often used ''within'' a particular industry or country. Industries in British English-speaking countries typically use the "gauge" spelling. is the pressure relative to the ambient pressure. Various #Units, units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the International System of Units, SI unit of pressure, the Pascal (unit), pascal (Pa), for example, is one newton (unit), newton per square metre (N/m2); similarly, the Pound (force), pound-force per square inch (Pound per square inch, psi, symbol lbf/in2) is the traditional unit of pressure in the imperial units, imperial and United States customary units, US customary systems. Pressure ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
National Institute Of Standards And Technology
The National Institute of Standards and Technology (NIST) is an agency of the United States Department of Commerce whose mission is to promote American innovation and industrial competitiveness. NIST's activities are organized into Outline of physical science, physical science laboratory programs that include Nanotechnology, nanoscale science and technology, engineering, information technology, neutron research, material measurement, and physical measurement. From 1901 to 1988, the agency was named the National Bureau of Standards. History Background The Articles of Confederation, ratified by the colonies in 1781, provided: The United States in Congress assembled shall also have the sole and exclusive right and power of regulating the alloy and value of coin struck by their own authority, or by that of the respective states—fixing the standards of weights and measures throughout the United States. Article 1, section 8, of the Constitution of the United States, ratified i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |