|
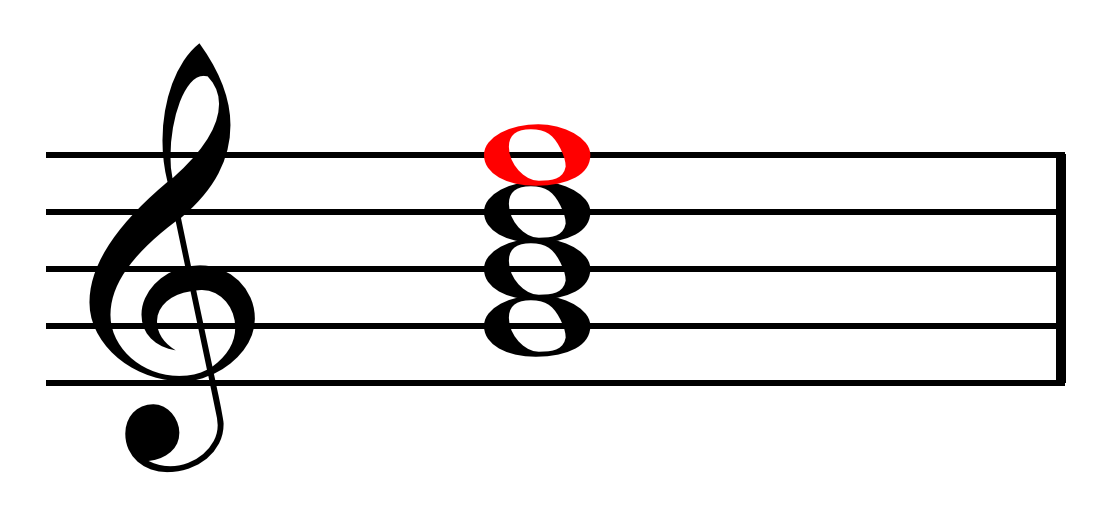
Viennese Trichord
In music theory, a Viennese trichord (also known as Viennese fourth chord and tritone-fourth chordDeLone, Richard, et al (1975). ''Aspects of 20th Century Music'', p. 348. Englewood Cliffs, New Jersey: Prentice-Hall .), named for the Second Viennese School, is a pitch set with prime form (0,1,6). Its Forte number is 3-5. The sets C–D–G and C–F–G are both examples of Viennese trichords, though they may be voiced in many ways. According to Henry Martin, " mposers such as Webern ... are partial to 016 trichords, given their 'more dissonant' inclusion of ics 1 and 6."Martin, Henry (Winter, 2000). "Seven Steps to Heaven: A Species Approach to Twentieth-Century Analysis and Composition", p. 149, ''Perspectives of New Music'', vol. 38, no. 1, pp. 129–168. In jazz and popular music, the chord formed by the inversion of the set usually has a dominant function, being the third, seventh, and added fourth/eleventh of a dominant chord with elided root Forte, Allen (2000). "Har ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root (chord)
In the music theory of harmony, the root is a specific Note (music), note that names and typifies a given chord (music), chord. Chords are often spoken about in terms of their root, their Chord quality, quality, and their Chord extensions, extensions. When a chord is named without reference to quality, it is assumed to be major chord, major—for example, a "C chord" refers to a C major triad, containing the notes C, E, and G. In a given harmonic context, the root of a chord need not be in bass note, the bass position, as chords may be Inversion (music), inverted while retaining the same name, and therefore the same root. In tertian harmonic theory, wherein chords can be considered stacks of third intervals (e.g. in common practice period, common practice tonality), the root of a chord is the Musical note, note on which the subsequent thirds are stacked. For instance, the root of a triad (music), triad such as E Minor is E, independently of the vertical order in which the three n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consonance And Dissonance
In music, consonance and dissonance are categorizations of simultaneous or successive sounds. Within the Western tradition, some listeners associate consonance with sweetness, pleasantness, and acceptability, and dissonance with harshness, unpleasantness, or unacceptability, although there is broad acknowledgement that this depends also on familiarity and musical expertise. The terms form a structural dichotomy in which they define each other by mutual exclusion: a consonance is what is not dissonant, and a dissonance is what is not consonant. However, a finer consideration shows that the distinction forms a gradation, from the most consonant to the most dissonant. In casual discourse, as German composer and music theorist Paul Hindemith stressed, : "The two concepts have never been completely explained, and for a thousand years the definitions have varied". The term ''sonance'' has been proposed to encompass or refer indistinctly to the terms ''consonance'' and ''dissonance''. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Walter Everett (musicologist)
Walter Everett is a music theorist specializing in popular music who teaches at the University of Michigan. His books include ''The Beatles as Musicians: Revolver through the Anthology'' (1999, ), which has been called "the most important work to appear on the Beatles thus far",The 2007/2008 Kjell Meling Award , ''Penn State Altoona''. and its follow-up volume, ''The Beatles as Musicians: The Quarry Men through Rubber Soul'' (2001). He also wrote ''The Foundations of Rock: From 'Blue Suede Shoes' to 'Suite: Judy Blue Eyes (2008, ) and has contributed to titles in the Cambridge Companions to Music series. Gary Burns, editor of the journal ''Popular Music and Society'', describes Everett's ''Beatles as Musicians'' volumes as a "monumental two-book set" that has furthered the field of musicological study begun in 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Allen Forte
Allen Forte (December 23, 1926 – October 16, 2014) was an American music theorist and musicologist. He was Battell Professor Emeritus of the Theory of Music at Yale University and specialized in 20th-century atonal music and music analysis. Early life and education Forte was born in Portland, Oregon. At the age of ten he appeared "on a ocalradio show as a solo pianist among a bevy of similarly youthful performers," where he played the music of Cole Porter and others. He was in the US Navy and served in the Pacific Theatre toward the end of World War II. Afterwards, he relocated to New York City to study music at Columbia University where he received his bachelor's, master's, and doctoral degrees. There, he studied composition with Otto Luening and Vladimir Ussachevsky, although his main interests were forming around music theory and analysis. Academic career In the late 1950s, Forte taught music at various New York institutions: Columbia University Teachers College, Man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root (chord)
In the music theory of harmony, the root is a specific Note (music), note that names and typifies a given chord (music), chord. Chords are often spoken about in terms of their root, their Chord quality, quality, and their Chord extensions, extensions. When a chord is named without reference to quality, it is assumed to be major chord, major—for example, a "C chord" refers to a C major triad, containing the notes C, E, and G. In a given harmonic context, the root of a chord need not be in bass note, the bass position, as chords may be Inversion (music), inverted while retaining the same name, and therefore the same root. In tertian harmonic theory, wherein chords can be considered stacks of third intervals (e.g. in common practice period, common practice tonality), the root of a chord is the Musical note, note on which the subsequent thirds are stacked. For instance, the root of a triad (music), triad such as E Minor is E, independently of the vertical order in which the three n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dominant Chord
In music, the dominant is the fifth scale degree () of the diatonic scale. It is called the ''dominant'' because it is second in importance to the first scale degree, the tonic. In the movable do solfège system, the dominant note is sung as "So(l)". The triad built on the dominant note is called the dominant chord. This chord is said to have dominant function, which means that it creates an instability that requires the tonic for resolution. Dominant triads, seventh chords, and ninth chords typically have dominant function. Leading-tone triads and leading-tone seventh chords may also have dominant function. Dominant chords In music theory, the dominant triad is a major chord, symbolized by the Roman numeral "V" in the major scale. In the natural minor scale, the triad is a minor chord, denoted by "v". However, in a minor key, the seventh scale degree is often raised by a half step ( to ), creating a major chord. These chords may also appear as seventh chord ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seventh (chord)
In music, the seventh factor (chord), factor of a chord (music), chord is the note (music), note or pitch (music), pitch seven scale degrees above the root (chord), root or tonality, tonal center.Riemann, Hugo. Dictionary of Music'. Trans. J.A. Shedlock. Augener, 1900. 730. When the seventh is the bass note, or lowest note, of the expressed chord, the chord is in third inversion . Conventionally, the seventh is fourth in importance to the root, fifth (chord), fifth, and third (chord), third, with third inversion being the third strongest Inversion (interval), inversion and the seventh variably minor or major. In jazz In jazz chords and theory, and classical music theory, the seventh is what defines a chord as a "seventh chord". Moreover, most triad (music), triads that appear in lead sheets or fake books can have sevenths added to them, using the performer's discretion and "ear". For example, if a tune is in the key of C, if there is a G chord, the chord-playing performer will ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Third (chord)
In music, the third factor of a chord is the note or pitch two scale degrees above the root or tonal center. When the third is the bass note, or lowest note, of the expressed triad, the chord is in first inversion. Use Conventionally, the third is third in importance to the root and fifth, with the third in all primary triads (I, IV, V and i, iv, v) being either major or minor. In jazz chords and theory, the third is required due to it determining chord quality. The third in both major and augmented chords is major (E in C) and the third in both minor and diminished chords is minor (E in C). Tenth In music and music theory, a tenth is the note ten scale degrees from the root of a chord and also the interval between the root and the tenth. Since there are only seven degrees in a diatonic scale the tenth degree is the same as the mediant and the interval of a tenth is a compound third. See also * List of third intervals Third interval may refer to one of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diatonic Function
In music, function (also referred to as harmonic function) is a term used to denote the relationship of a chord"Function", unsigned article, ''Grove Music Online'', . or a scale degree to a tonal centre. Two main theories of tonal functions exist today: * The German theory created by Hugo Riemann in his ''Vereinfachte Harmonielehre'' of 1893, which soon became an international success (English and Russian translations in 1896, French translation in 1899), and which is the theory of functions properly speaking."It was Riemann who coined the term 'function' in ''Vereinfachte Harmonielehre'' (1893) to describe relations between the dominant and subdominant harmonies and the referential tonic: he borrowed the word from mathematics, where it was used to designate the correlation of two variables, an 'argument' and a 'value'". Brian Hyer, "Tonality", ''Grove Music Online'', . Riemann described three abstract tonal "functions", tonic, dominant and subdominant, denoted by the letters T, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dominant (music)
In music Music is the arrangement of sound to create some combination of Musical form, form, harmony, melody, rhythm, or otherwise Musical expression, expressive content. Music is generally agreed to be a cultural universal that is present in all hum ..., the dominant is the fifth degree (music), scale degree () of the diatonic scale. It is called the ''dominant'' because it is second in importance to the first scale degree, the tonic (music), tonic. In the Solfège#Movable do solf%C3%A8ge, movable do solfège system, the dominant note is sung as "So(l)". The Triad (music), triad built on the dominant note is called the dominant chord. This chord is said to have dominant Function (music), function, which means that it creates an instability that requires the tonic (music), tonic for resolution (music), resolution. Dominant triads, Seventh chord, seventh chords, and Ninth chord, ninth chords typically have dominant function. Leading-tone triad, Leading-tone triads and Leadin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inversion (music)
In music theory, an inversion is a rearrangement of the top-to-bottom elements in an interval, a chord, a melody, or a group of contrapuntal lines of music. In each of these cases, "inversion" has a distinct but related meaning. The concept of inversion also plays an important role in musical set theory. Intervals An interval is inverted by raising or lowering either of the notes by one or more octaves so that the higher note becomes the lower note and vice versa. For example, the inversion of an interval consisting of a C with an E above it (the third measure below) is an E with a C above it – to work this out, the C may be moved up, the E may be lowered, or both may be moved. : The tables to the right show the changes in interval quality and interval number under inversion. Thus, perfect intervals remain perfect, major intervals become minor and vice versa, and augmented intervals become diminished and vice versa. (Doubly diminished intervals become doubly augme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Popular Music
Popular music is music with wide appeal that is typically distributed to large audiences through the music industry. These forms and styles can be enjoyed and performed by people with little or no musical training.Popular Music. (2015). ''Funk & Wagnalls New World Encyclopedia'' As a kind of popular art, it stands in contrast to art music. Art music was historically disseminated through the performances of written music, although since the beginning of the recording industry, it is also disseminated through sound recording, recordings. Traditional music forms such as early blues songs or hymns were passed along orally, or to smaller, local audiences. The original application of the term is to music of the 1880s Tin Pan Alley period in the United States. Although popular music sometimes is known as "pop music", the two terms are not interchangeable. Popular music is a generic term for a wide variety of genres of music that appeal to the tastes of a large segment of the populati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |