|
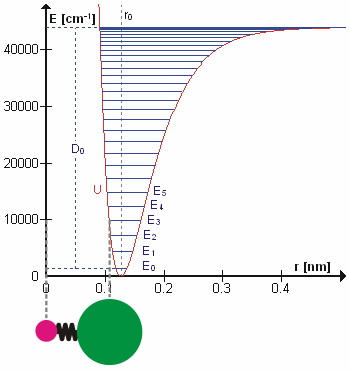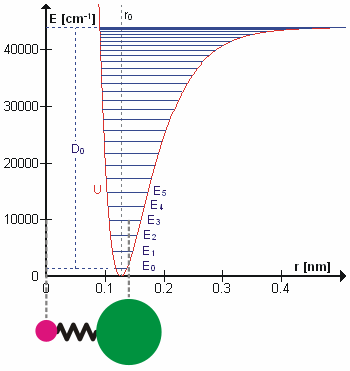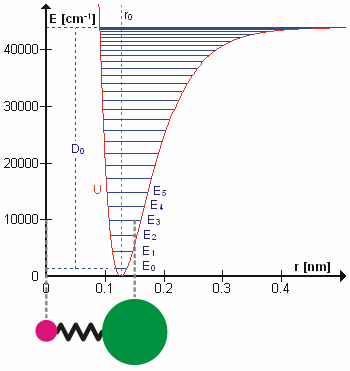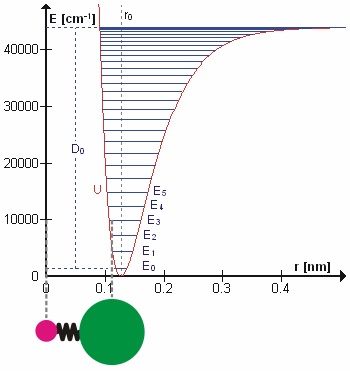
Vibrational Partition Function
The vibrational partition functionDonald A. McQuarrie, ''Statistical Mechanics'', Harper & Row, 1973 traditionally refers to the component of the canonical partition function resulting from the vibrational degrees of freedom of a system. The vibrational partition function is only well-defined in model systems where the vibrational motion is relatively uncoupled with the system's other degrees of freedom. Definition For a system (such as a molecule or solid) with uncoupled vibrational modes the vibrational partition function is defined by Q_\text(T) = \prod_j where T is the absolute temperature of the system, k_B is the Boltzmann constant, and E_ is the energy of the ''j''th mode when it has vibrational quantum number n = 0, 1, 2, \ldots . For an isolated molecule of ''N'' atoms, the number of vibrational modes (i.e. values of ''j'') is for linear molecules and for non-linear ones.G. Herzberg, ''Infrared and Raman Spectra'', Van Nostrand Reinhold, 1945 In crystals, the vib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Partition Function
The adjective canonical is applied in many contexts to mean 'according to the canon (basic principle), canon' the standard (metrology), standard, rule or primary source that is accepted as authoritative for the body of knowledge or literature in that context. In mathematics, ''canonical example'' is often used to mean 'archetype'. Science and technology * Canonical form, a natural unique representation of an object, or a preferred notation for some object Mathematics * * Canonical coordinates, sets of coordinates that can be used to describe a physical system at any given point in time * Canonical map, a morphism that is uniquely defined by its main property * Canonical polyhedron, a polyhedron whose edges are all tangent to a common sphere, whose center is the average of its vertices * Canonical ring, a graded ring associated to an algebraic variety * Canonical injection, in set theory * Canonical representative, in set theory a standard member of each element of a set partitio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion. Thermodynamic temperature is typically expressed using the Kelvin scale, where the unit of measurement is the ''kelvin'' (unit symbol: K). The Kelvin scale uses the same degree interval as the Celsius scale but is offset so that 0 K corresponds to absolute zero. For comparison, a temperature of 295 K corresponds to 21.85 °C and 71.33 °F. Another absolute scale of temperature is the Rankine scale, which is based on the Fahrenheit degree interval. Historically, thermodynamic temperature was defined by Lord Kelvin in terms of a macroscopic relation between Work (thermodynamics), thermodynamic work and Heat, heat transfer as defined in thermodynamics, but the kelvin was redefined by international agreement in 2019 in terms of phenomena that are now understood as man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the molar gas constant, in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating Johnson–Nyquist noise, thermal noise in resistors. The Boltzmann constant has Dimensional analysis, dimensions of energy divided by temperature, the same as entropy and heat capacity. It is named after the Austrian scientist Ludwig Boltzmann. As part of the 2019 revision of the SI, the Boltzmann constant is one of the seven "Physical constant, defining constants" that have been defined so as to have exact finite decimal values in SI units. They are used in various combinations to define the seven SI base units. The Boltzmann constant is defined to be exactly joules per kelvin, with the effect of defining the SI unit ke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Vibration
A molecular vibration is a Periodic function, periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The infrared spectroscopy correlation table, typical vibrational frequencies range from less than 1013 hertz, Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 μm. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of parts of the molecule. In general, a non-linear molecule with ''N'' atoms has vibrational mode, normal modes of vibration, but a ''linear'' molecule has modes, because rotation about the molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration, since it can only stretch or compress the single bond. A molecular vibration is excited when the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phonon
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. In the context of optically trapped objects, the quantized vibration mode can be defined as phonons as long as the modal wavelength of the oscillation is smaller than the size of the object. A type of quasiparticle in physics, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves. The study of phonons is an important part of condensed matter physics. They play a major role in many of the physical properties of condensed matter systems, such as thermal conductivity and electrical conductivity, as well as in models of neutron scattering and related effects. The concept of phonons was introduced in 1930 by Soviet physicist Igor Tamm. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Mode
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies. These fixed frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge, or molecule, has a set of normal modes and their natural frequencies that depend on its structure, materials and boundary conditions. The most general motion of a linear system is a superposition of its normal modes. The modes are normal in the sense that they can move independently, that is to say that an excitation of one mode will never cause motion of a different mode. In mathematical terms, normal modes are orthogonal to each other. General definitions Mode In the wave theory of physics and engineering, a mode in a dynamical system is a standing wave st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Harmonic Oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known. One-dimensional harmonic oscillator Hamiltonian and energy eigenstates The Hamiltonian of the particle is: \hat H = \frac + \frac k ^2 = \frac + \frac m \omega^2 ^2 \, , where is the particle's mass, is the force constant, \omega = \sqrt is the angular frequency of the oscillator, \hat is the position operator (given by in the coordinate basis), and \hat is the momentum operator (given by \hat p = -i \hbar \, \partial / \partial x in the coordinate basis). The first term in the Hamiltonian represents the kinetic energy of the particle, and the second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planck Constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum. The constant was postulated by Max Planck in 1900 as a proportionality constant needed to explain experimental black-body radiation. Planck later referred to the constant as the "quantum of Action (physics), action". In 1905, Albert Einstein associated the "quantum" or minimal element of the energy to the electromagnetic wave itself. Max Planck received the 1918 Nobel Prize in Physics "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta". In metrology, the Planck constant is used, together with other constants, to define the kilogram, the SI unit of mass. The SI units are defined in such a way that, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of reciprocal length, expressed in SI units of cycles per metre or reciprocal metre (m−1). Angular wavenumber, defined as the wave phase divided by time, is a quantity with dimension of angle per length and SI units of radians per metre. They are analogous to temporal frequency, respectively the '' ordinary frequency'', defined as the number of wave cycles divided by time (in cycles per second or reciprocal seconds), and the ''angular frequency'', defined as the phase angle divided by time (in radians per second). In multidimensional systems, the wavenumber is the magnitude of the '' wave vector''. The space of wave vectors is called ''reciprocal space''. Wave numbers and wave vectors play an essential role in optics and the physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speed Of Light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time interval of second. The speed of light is invariant (physics), the same for all observers, no matter their relative velocity. It is the upper limit for the speed at which Information#Physics_and_determinacy, information, matter, or energy can travel through Space#Relativity, space. All forms of electromagnetic radiation, including visible light, travel at the speed of light. For many practical purposes, light and other electromagnetic waves will appear to propagate instantaneously, but for long distances and sensitive measurements, their finite speed has noticeable effects. Much starlight viewed on Earth is from the distant past, allowing humans to study the history of the universe by viewing distant objects. When Data communication, comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Function (mathematics)
The partition function or configuration integral, as used in probability theory, information theory and dynamical systems, is a generalization of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann distribution. The partition function occurs in many problems of probability theory because, in situations where there is a natural symmetry, its associated probability measure, the Gibbs measure, has the Markov property. This means that the partition function occurs not only in physical systems with translation symmetry, but also in such varied settings as neural networks (the Hopfield network), and applications such as genomics, corpus linguistics and artificial intelligence, which employ Markov networks, and Markov logic networks. The Gibbs measure is also the unique measure that has the property of maximizing the entropy for a fixed expectation value of the energy; this under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |