|
Versor Posterior Analytics
In mathematics, a versor is a quaternion of norm one, also known as a unit quaternion. Each versor has the form :u = \exp(a\mathbf) = \cos a + \mathbf \sin a, \quad \mathbf^2 = -1, \quad a \in ,\pi where the r2 = −1 condition means that r is an imaginary unit. There is a sphere of imaginary units in the quaternions. Note that the expression for a versor is just Euler's formula for the imaginary unit r. In case (a right angle), then u = \mathbf, and it is called a ''right versor''. The mapping q \to u^ q u corresponds to 3-dimensional rotation, and has the angle 2''a'' about the axis r in axis–angle representation. The collection of versors, with quaternion multiplication, forms a group, and appears as a 3-sphere in the 4-dimensional quaternion algebra. Presentation on 3- and 2-spheres Hamilton denoted the versor of a quaternion ''q'' by the symbol U ''q''. He was then able to display the general quaternion in polar coordinate form : ''q'' = T ''q'' U ''q'', where T ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
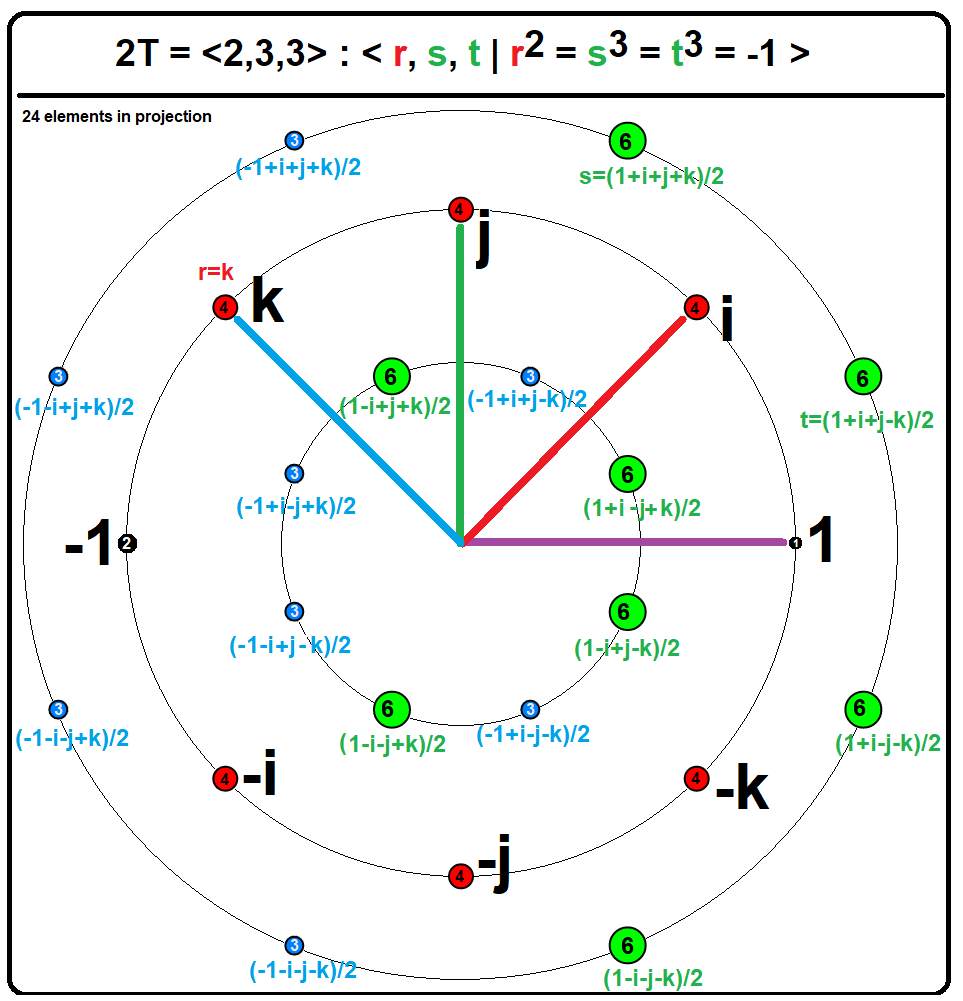
Hurwitz Quaternion
In mathematics, a Hurwitz quaternion (or Hurwitz integer) is a quaternion whose components are ''either'' all integers ''or'' all half-integers (halves of odd integers; a mixture of integers and half-integers is excluded). The set of all Hurwitz quaternions is :H = \left\. That is, either ''a'', ''b'', ''c'', ''d'' are all integers, or they are all half-integers. ''H'' is closed under quaternion multiplication and addition, which makes it a subring of the ring of all quaternions H. Hurwitz quaternions were introduced by . A Lipschitz quaternion (or Lipschitz integer) is a quaternion whose components are all integers. The set of all Lipschitz quaternions :L = \left\ forms a subring of the Hurwitz quaternions ''H''. Hurwitz integers have the advantage over Lipschitz integers that it is possible to perform Euclidean division on them, obtaining a small remainder. Both the Hurwitz and Lipschitz quaternions are examples of noncommutative domains which are not division rings. Str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intersection Point
In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, their intersection is the point at which they meet. More generally, in set theory, the intersection of sets is defined to be the set of elements which belong to all of them. Unlike the Euclidean definition, this does not presume that the objects under consideration lie in a common space. It simply means the overlapping area of two or more objects or geometries. Intersection is one of the basic concepts of geometry. An intersection can have various geometric shapes, but a point is the most common in a plane geometry. Incidence geometry defines an intersection (usually, of flats) as an object of lower dimension that is incident to each of the original objects. In this approach an intersection can be sometimes undefined, such as for parallel lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟂. Perpendicular intersections can happen between two lines (or two line segments), between a line and a plane, and between two planes. ''Perpendicular'' is also used as a noun: a perpendicular is a line which is perpendicular to a given line or plane. Perpendicularity is one particular instance of the more general mathematical concept of '' orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its '' normal vector''. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Mathematical Physics
The ''Journal of Mathematical Physics'' is a peer-reviewed journal published monthly by the American Institute of Physics devoted to the publication of papers in mathematical physics. The journal was first published bimonthly beginning in January 1960; it became a monthly publication in 1963. The current editor is Jan Philip Solovej from University of Copenhagen The University of Copenhagen (, KU) is a public university, public research university in Copenhagen, Copenhagen, Denmark. Founded in 1479, the University of Copenhagen is the second-oldest university in Scandinavia, after Uppsala University. .... Its 2018 Impact Factor is 1.355 Abstracting and indexing This journal is indexed by the following services: 2013. References External ...
|
Equipollence (geometry)
In Euclidean geometry, equipollence is a homogeneous relation between directed line segments. Two segments are said to be ''equipollent'' when they have the same length and direction. Two equipollent segments are parallel but not necessarily colinear nor overlapping. For example, a segment ''AB'', from point ''A'' to point ''B'', has the opposite direction to segment ''BA''; thus ''AB'' and ''BA'' are equipollent. Parallelogram property A property of Euclidean spaces is the parallelogram property of vectors: If two segments are equipollent, then they form two sides of a (possibly degenerate) parallelogram: History The concept of equipollent line segments was advanced by Giusto Bellavitis in 1835. Subsequently, the term vector was adopted for a class of equipollent line segments. Bellavitis's use of the idea of a relation to compare different but similar objects has become a common mathematical technique, particularly in the use of equivalence relations. Bellavitis us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an Circular arc, arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless unit, dimensionless SI derived unit,: "The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units." defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as . Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing. Definition One radian is defined as the angle at the center of a circle in a plane that wikt:subtend, subtends an arc whose length equals the radius of the circle. More generally, the magnit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Sphere
In mathematics, a unit sphere is a sphere of unit radius: the locus (mathematics), set of points at Euclidean distance 1 from some center (geometry), center point in three-dimensional space. More generally, the ''unit -sphere'' is an n-sphere, -sphere of unit radius in -dimensional Euclidean space; the unit circle is a special case, the unit -sphere in the Euclidean plane, plane. An (Open set, open) unit ball is the region inside of a unit sphere, the set of points of distance less than 1 from the center. A sphere or ball with unit radius and center at the origin (mathematics), origin of the space is called ''the'' unit sphere or ''the'' unit ball. Any arbitrary sphere can be transformed to the unit sphere by a combination of translation (geometry), translation and scaling (geometry), scaling, so the study of spheres in general can often be reduced to the study of the unit sphere. The unit sphere is often used as a model for spherical geometry because it has constant sectional cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Discussion Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry are the natural analog of straight lines in Euclidean space. For any pair of distinct non- antipodal points on the sphere, there is a unique great circle passing through both. (Every great circle through any point also passes through its antipodal point, so there are infinitely many great circles through two antipodal points.) The shorter of the two great-circle arcs between two distinct points on the sphere is called the ''minor arc'', and is the shortest surface-path between them. Its arc length is the great-circle distance between the points (the intrinsic distance on a sphere), and is proportional to the measure of the central angle formed by the two points and the center of the sphere. A great circle is the largest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Geometry
300px, A sphere with a spherical triangle on it. Spherical geometry or spherics () is the geometry of the two-dimensional surface of a sphere or the -dimensional surface of higher dimensional spheres. Long studied for its practical applications to astronomy, navigation, and geodesy, spherical geometry and the metrical tools of spherical trigonometry are in many respects analogous to Euclidean plane geometry and trigonometry, but also have some important differences. The sphere can be studied either ''extrinsically'' as a surface embedded in 3-dimensional Euclidean space (part of the study of solid geometry), or ''intrinsically'' using methods that only involve the surface itself without reference to any surrounding space. Principles In plane (Euclidean) geometry, the basic concepts are points and (straight) lines. In spherical geometry, the basic concepts are points and great circles. However, two great circles on a plane intersect in two antipodal points, unlike coplan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special case of an ''arc (geometry), arc'', with zero curvature. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using an overline (vinculum (symbol), vinculum) above the symbols for the two endpoints, such as in . Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. Wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc (geometry)
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line (geometry), line, but that does not have to be Linearity, straight. Intuitively, a curve may be thought of as the trace left by a moving point (geometry), point. This is the definition that appeared more than 2000 years ago in Euclid's Elements, Euclid's ''Elements'': "The [curved] line is […] the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which […] will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image (mathematics), image of an interval (mathematics), interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this artic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |