|
Vandermonde Identity
In combinatorics, Vandermonde's identity (or Vandermonde's convolution) is the following identity for binomial coefficients: :=\sum_^r for any nonnegative integers ''r'', ''m'', ''n''. The identity is named after Alexandre-Théophile Vandermonde (1772), although it was already known in 1303 by the Chinese mathematician Zhu Shijie.See for the history. There is a ''q''-analog to this theorem called the ''q''-Vandermonde identity. Vandermonde's identity can be generalized in numerous ways, including to the identity : = \sum_ \cdots . Proofs Algebraic proof In general, the product of two polynomials with degrees ''m'' and ''n'', respectively, is given by :\biggl(\sum_^m a_ix^i\biggr) \biggl(\sum_^n b_jx^j\biggr) = \sum_^\biggl(\sum_^r a_k b_\biggr) x^r, where we use the convention that ''ai'' = 0 for all integers ''i'' > ''m'' and ''bj'' = 0 for all integers ''j'' > ''n''. By the binomial theorem, :(1+x)^ = \sum_^ x^r. U ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science. Combinatorics is well known for the breadth of the problems it tackles. Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving an ''ad hoc'' solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Series
In mathematics, the binomial series is a generalization of the binomial formula to cases where the exponent is not a positive integer: where \alpha is any complex number, and the power series on the right-hand side is expressed in terms of the (generalized) binomial coefficients :\binom = \frac. The binomial series is the MacLaurin series for the function f(x)=(1+x)^\alpha. It converges when , x, - 1 is assumed. On the other hand, the series does not converge if , x, =1 and \operatorname(\alpha) \le - 1 , again by formula (). Alternatively, we may observe that for all j, \left, \fracj - 1 \ \ge 1 - \fracj \ge 1 . Thus, by formula (), for all k, \left, \ \ge 1 . This completes the proof of (iii). Turning to (iv), we use identity () above with x=-1 and \alpha-1 in place of \alpha, along with formula (), to obtain :\sum_^n \! (-1)^k = \! (-1)^n= \frac1 (1+o(1)) as n\to\infty. Assertion (iv) now follows from the asymptotic behavior of the sequence n^ = e^. (Precisely, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factorial And Binomial Topics
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial: \begin n! &= n \times (n-1) \times (n-2) \times (n-3) \times \cdots \times 3 \times 2 \times 1 \\ &= n\times(n-1)!\\ \end For example, 5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. The value of 0! is 1, according to the convention for an empty product. Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book ''Sefer Yetzirah''. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of n distinct objects: there In mathematical analysis, factorials are used in power series for the exponential function an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hockey-stick Identity
In combinatorics, the hockey-stick identity, Christmas stocking identity, boomerang identity, Fermat's identity or Chu's Theorem, states that if n \geq r \ge 0 are integers, then : \binom + \binom + \binom + \cdots + \binom = \binom. The name stems from the graphical representation of the identity on Pascal's triangle: when the addends represented in the summation and the sum itself are highlighted, the shape revealed is vaguely reminiscent of those objects (see hockey stick, Christmas stocking). Formulations Using sigma notation, the identity states : \sum^n_= \qquad \text n,r\in\mathbb, \quad n\geq r or equivalently, the mirror-image by the substitution j\to i-r, and by using the identify =: : \sum^_=\sum^_= \qquad \text n,r\in\mathbb, \quad n\geq r. Proofs Inductive and algebraic proofs The inductive and algebraic proofs both make use of Pascal's identity: :=+. Inductive proof This identity can be proven by mathematical induction on n. Base case Let n=r; :\sum^n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal's Identity
In mathematics, Pascal's rule (or Pascal's formula) is a combinatorics, combinatorial identity (mathematics), identity about binomial coefficients. The binomial coefficients are the numbers that appear in Pascal's triangle. Pascal's rule states that for natural number, positive integers ''n'' and ''k'', + = , where \tbinom is the binomial coefficient, namely the coefficient of the term in the polynomial expansion, expansion of . There is no restriction on the relative sizes of and ; in particular, the above identity remains valid when since \tbinom = 0 whenever . Together with the boundary conditions \tbinom = \tbinom= 1 for all nonnegative integers ''n'', Pascal's rule determines that \binom = \frac, for all integers . In this sense, Pascal's rule is the recurrence relation that defines the binomial coefficients. Pascal's rule can also be generalized to apply to multinomial coefficients. Combinatorial proof Blaise Pascal, Pascal's rule has an intuitive combinatorial me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
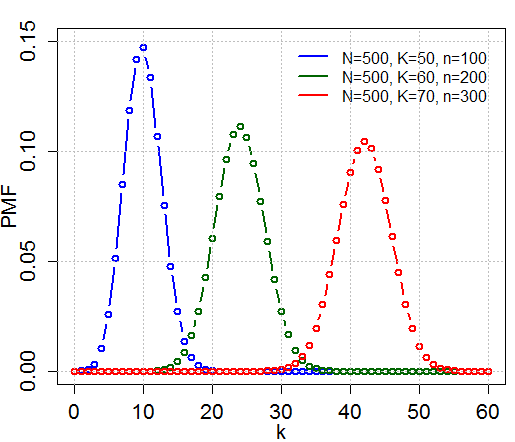
Hypergeometric Distribution
In probability theory and statistics, the hypergeometric distribution is a Probability distribution#Discrete probability distribution, discrete probability distribution that describes the probability of k successes (random draws for which the object drawn has a specified feature) in n draws, ''without'' replacement, from a finite Statistical population, population of size N that contains exactly K objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of k successes in n draws ''with'' replacement. Definitions Probability mass function The following conditions characterize the hypergeometric distribution: * The result of each draw (the elements of the population being sampled) can be classified into one of Binary variable, two mutually exclusive categories (e.g. Pass/Fail or Employed/Unemployed). * The probability of a success changes on each draw, as each draw decreases the population ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rothe–Hagen Identity
In mathematics, the Rothe–Hagen identity is a mathematical identity valid for all complex numbers (x, y, z) except where its denominators vanish: :\sum_^n\frac\frac=\frac. It is a generalization of Vandermonde's identity, and is named after Heinrich August Rothe and Johann Georg Hagen Johann (John) Georg Hagen (March 6, 1847 – September 6, 1930) was an Austrian Society of Jesus, Jesuit priest and astronomer. After serving as Director of the Georgetown University Astronomical Observatory, Georgetown University Observator .... References *. *. See especially pp. 89–91. *. As cited by . *. *. As cited by . Factorial and binomial topics Algebraic identities Complex analysis {{mathapplied-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined for all complex numbers z except non-positive integers, and for every positive integer z=n, \Gamma(n) = (n-1)!\,.The gamma function can be defined via a convergent improper integral for complex numbers with positive real part: \Gamma(z) = \int_0^\infty t^ e^\textt, \ \qquad \Re(z) > 0\,.The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is holomorphic function, holomorphic except at zero and the negative integers, where it has simple Zeros and poles, poles. The gamma function has no zeros, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypergeometric Function
In mathematics, the Gaussian or ordinary hypergeometric function 2''F''1(''a'',''b'';''c'';''z'') is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation. For systematic lists of some of the many thousands of published identities involving the hypergeometric function, see the reference works by and . There is no known system for organizing all of the identities; indeed, there is no known algorithm that can generate all identities; a number of different algorithms are known that generate different series of identities. The theory of the algorithmic discovery of identities remains an active research topic. History The term "hypergeometric series" was first used by John Wallis in his 1655 book ''Arithmetica Infinitor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Type
In mathematics, a polynomial sequence, i.e., a sequence of polynomials indexed by non-negative integers \left\ in which the index of each polynomial equals its degree, is said to be of binomial type if it satisfies the sequence of identities :p_n(x+y)=\sum_^n\, p_k(x)\, p_(y). Many such sequences exist. The set of all such sequences forms a Lie group under the operation of umbral composition, explained below. Every sequence of binomial type may be expressed in terms of the Bell polynomials. Every sequence of binomial type is a Sheffer sequence (but most Sheffer sequences are not of binomial type). Polynomial sequences put on firm footing the vague 19th century notions of umbral calculus. Examples * In consequence of this definition the binomial theorem can be stated by saying that the sequence \ is of binomial type. * The sequence of " lower factorials" is defined by(x)_n=x(x-1)(x-2)\cdot\cdots\cdot(x-n+1).(In the theory of special functions, this same notation denotes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |