|
Uniform Limit Theorem
In mathematics, the uniform limit theorem states that the uniform limit of any sequence of continuous functions is continuous. Statement More precisely, let ''X'' be a topological space, let ''Y'' be a metric space, and let ƒ''n'' : ''X'' → ''Y'' be a sequence of functions converging uniformly to a function ƒ : ''X'' → ''Y''. According to the uniform limit theorem, if each of the functions ƒ''n'' is continuous, then the limit ƒ must be continuous as well. This theorem does not hold if uniform convergence is replaced by pointwise convergence. For example, let ƒ''n'' : , 1nbsp;→ R be the sequence of functions ƒ''n''(''x'') = ''xn''. Then each function ƒ''n'' is continuous, but the sequence converges pointwise to the discontinuous function ƒ that is zero on closed subset of ''YX'' under the uniform metric. In the case where ''Y'' is Complete metric space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Drini Nonuniformconvergence SVG
The Drin (; or ; ) is a river in Southeastern Europe with two major tributaries – the White Drin and the Black Drin and two distributaries – one discharging into the Adriatic Sea, in the Gulf of Drin and the other into the Buna River. Its catchment area extends across Albania, Kosovo, Serbia, Greece, Montenegro and North Macedonia and is home to more than 1.6 million people. The river and its tributaries form the Gulf of Drin, an ocean basin that encompasses the northern Albanian Adriatic Sea Coast. At long, the Drin is the Rivers of Albania, longest river of Albania and its tributaries cross through both Kosovo and North Macedonia. Its northern tributary, the White Drin starts from the foothills of Žljeb mountain, Žljeb, at White Drin Waterfall in west Kosovo, and flows generally south, whereas its southern tributary, the Black Drin originates from Ohrid lake in the town of Struga, North Macedonia and flows north. Both tributaries' confluence occurs near Kukës in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach Space
In mathematics, more specifically in functional analysis, a Banach space (, ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space. Banach spaces are named after the Polish mathematician Stefan Banach, who introduced this concept and studied it systematically in 1920–1922 along with Hans Hahn and Eduard Helly. Maurice René Fréchet was the first to use the term "Banach space" and Banach in turn then coined the term " Fréchet space". Banach spaces originally grew out of the study of function spaces by Hilbert, Fréchet, and Riesz earlier in the century. Banach spaces play a central role in functional analysis. In other areas of analysis, the spaces under study are often Banach spaces. Definition A Banach space is a complete nor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prentice Hall
Prentice Hall was a major American publishing#Textbook_publishing, educational publisher. It published print and digital content for the 6–12 and higher-education market. It was an independent company throughout the bulk of the twentieth century. In its last few years it was owned by, then absorbed into, Savvas Learning Company. In the Web era, it distributed its technical titles through the Safari Books Online e-reference service for some years. History On October 13, 1913, law professor Charles Gerstenberg and his student Richard Ettinger founded Prentice Hall. Gerstenberg and Ettinger took their mothers' maiden names, Prentice and Hall, to name their new company. At the time the name was usually styled as Prentice-Hall (as seen for example on many title pages), per an orthographic norm for Dash#Relationships and connections, coordinate elements within such compounds (compare also ''McGraw-Hill'' with later styling as ''McGraw Hill''). Prentice-Hall became known as a publi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of Degeneracy (mathematics)#Triangle, degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If , , and are the lengths of the sides of a triangle then the triangle inequality states that :c \leq a + b , with equality only in the degenerate case of a triangle with zero area. In Euclidean geometry and some other geometries, the triangle inequality is a theorem about vectors and vector lengths (Norm (mathematics), norms): :\, \mathbf u + \mathbf v\, \leq \, \mathbf u\, + \, \mathbf v\, , where the length of the third side has been replaced by the length of the vector sum . When and are real numbers, they can be viewed as vectors in \R^1, and the triang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood (or neighborhood) is one of the basic concepts in a topological space. It is closely related to the concepts of open set and Interior (topology), interior. Intuitively speaking, a neighbourhood of a point is a Set (mathematics), set of points containing that point where one can move some amount in any direction away from that point without leaving the set. Definitions Neighbourhood of a point If X is a topological space and p is a point in X, then a neighbourhood of p is a subset V of X that includes an open set U containing p, p \in U \subseteq V \subseteq X. This is equivalent to the point p \in X belonging to the Interior (topology)#Interior point, topological interior of V in X. The neighbourhood V need not be an open subset of X. When V is open (resp. closed, compact, etc.) in X, it is called an (resp. closed neighbourhood, compact neighbourhood, etc.). Some authors require neighbourhoods to be open, so i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
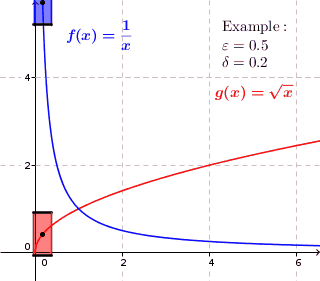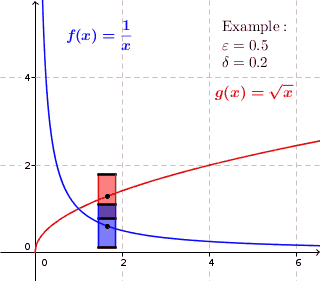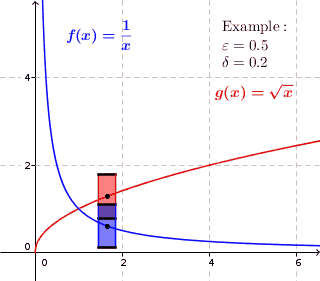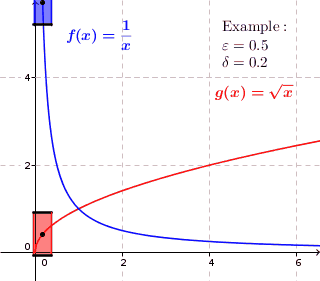
Uniform Continuity
In mathematics, a real function f of real numbers is said to be uniformly continuous if there is a positive real number \delta such that function values over any function domain interval of the size \delta are as close to each other as we want. In other words, for a uniformly continuous real function of real numbers, if we want function value differences to be less than any positive real number \varepsilon, then there is a positive real number \delta such that , f(x) - f(y), 0 there exists a real number \delta > 0 such that for every x,y \in X with d_1(x,y) 0 such that for every x,y \in X , , x - y, 0 \; \forall x \in X \; \forall y \in X : \, d_1(x,y) 0 , \forall x \in X , and \forall y \in X ) are used. * Equivalently, f is uniformly continuous if it admits a modulus of continuity. Definition of (ordinary) continuity * f is called continuous \underline if for every real number \varepsilon > 0 there exists a real number \delta > 0 such that for every y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Norm
In mathematical analysis, the uniform norm (or ) assigns, to real- or complex-valued bounded functions defined on a set , the non-negative number :\, f\, _\infty = \, f\, _ = \sup\left\. This norm is also called the , the , the , or, when the supremum is in fact the maximum, the . The name "uniform norm" derives from the fact that a sequence of functions converges to under the metric derived from the uniform norm if and only if converges to uniformly. If is a continuous function on a closed and bounded interval, or more generally a compact set, then it is bounded and the supremum in the above definition is attained by the Weierstrass extreme value theorem, so we can replace the supremum by the maximum. In this case, the norm is also called the . In particular, if is some vector such that x = \left(x_1, x_2, \ldots, x_n\right) in finite dimensional coordinate space, it takes the form: :\, x\, _\infty := \max \left(\left, x_1\ , \ldots , \left, x_n\\right). This is c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Metric Space
In mathematical analysis, a metric space is called complete (or a Cauchy space) if every Cauchy sequence of points in has a limit that is also in . Intuitively, a space is complete if there are no "points missing" from it (inside or at the boundary). For instance, the set of rational numbers is not complete, because e.g. \sqrt is "missing" from it, even though one can construct a Cauchy sequence of rational numbers that converges to it (see further examples below). It is always possible to "fill all the holes", leading to the ''completion'' of a given space, as explained below. Definition Cauchy sequence A sequence x_1, x_2, x_3, \ldots of elements from X of a metric space (X, d) is called Cauchy if for every positive real number r > 0 there is a positive integer N such that for all positive integers m, n > N, d(x_m, x_n) < r. Complete space A metric space is complete if any of the following equivalent conditions are satisfied: #Every Cauchy seq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Metric
In mathematical analysis, the uniform norm (or ) assigns, to real- or complex-valued bounded functions defined on a set , the non-negative number :\, f\, _\infty = \, f\, _ = \sup\left\. This norm is also called the , the , the , or, when the supremum is in fact the maximum, the . The name "uniform norm" derives from the fact that a sequence of functions converges to under the metric derived from the uniform norm if and only if converges to uniformly. If is a continuous function on a closed and bounded interval, or more generally a compact set, then it is bounded and the supremum in the above definition is attained by the Weierstrass extreme value theorem, so we can replace the supremum by the maximum. In this case, the norm is also called the . In particular, if is some vector such that x = \left(x_1, x_2, \ldots, x_n\right) in finite dimensional coordinate space, it takes the form: :\, x\, _\infty := \max \left(\left, x_1\ , \ldots , \left, x_n\\right). This is cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |