|
Time-varying Microscale Model
The time-varying microscale (TVM) model is a microscale diagnostic model specifically designed to compute data for extremely high-resolution mapping (tens of meters to a few hundred meters) without the high computational costs of running a mesoscale numerical weather prediction (NWP) model such as weather research and forecasting model (WRF). TVM uses high-resolution land surface data to calculate the effects of microscale terrain features, near-surface roughness features, and other terrain blocking effects typically left unresolved by coarser mesoscale NWP models. Microscale terrain features are resolved using a kinematic terrain adjustment, near-surface roughness features are resolved using a log-profile surface roughness adjustment, and a Froude number adjustment is applied to calculate terrain-blocking effects on wind flow. All of these effects are computed at each time-step in the study period and based not only on wind speed and elevation, but on quantities such as wind d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Microscale
The micrometre (Commonwealth English as used by the International Bureau of Weights and Measures; SI symbol: μm) or micrometer (American English), also commonly known by the non-SI term micron, is a unit of length in the International System of Units (SI) equalling (SI standard prefix "micro-" = ); that is, one millionth of a metre (or one thousandth of a millimetre, , or about ). The nearest smaller common SI unit is the nanometre, equivalent to one thousandth of a micrometre, one millionth of a millimetre or one billionth of a metre (). The micrometre is a common unit of measurement for wavelengths of infrared radiation as well as sizes of biological cells and bacteria, and for grading wool by the diameter of the fibres. The width of a single human hair ranges from approximately 20 to . Examples Between 1 μm and 10 μm: * 1–10 μm – length of a typical bacterium * 3–8 μm – width of strand of spider web silk * 5 μm – length of a typical hum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diagnostic Model
In a physical (and especially geophysical) simulation context, a diagnostic equation (or diagnostic model) is an equation (or model) that links the values of these variables simultaneously, either because the equation (or model) is time-independent, or because the variables all refer to the values they have at the identical time. This is by opposition to a prognostic equation. For instance, the so-called ideal gas law (''PV'' = ''nRT'') of classical thermodynamics relates the state variables of that gas, all estimated at the same time. It is understood that the values of any one of these variables can change in time, but the relation between these variables will remain valid at each and every particular instant, which implies that one variable cannot change its value without the value of another variable also being affected. References * James R. Holton (2004) ''An Introduction to Dynamic Meteorology'', Academic Press, International Geophysics Series Volume 88, Fourth Edition, 535 p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mesoscale Meteorology
Mesoscale meteorology is the study of weather systems and processes at horizontal scales of approximately to several hundred kilometres. It is smaller than synoptic scale meteorology, synoptic-scale systems (1,000 km or larger) but larger than Microscale meteorology, microscale (less than 1 km). At the small end, it includes storm-scale phenomena (the size of an individual thunderstorm). Examples of mesoscale weather systems are sea breezes, squall lines, and mesoscale convective complexes. Vertical velocity often equals or exceeds horizontal velocities in mesoscale meteorological systems due to nonhydrostatic processes such as buoyant acceleration of a rising thermal or acceleration through a narrow mountain pass. Classification The History of weather forecasting, earliest networks of weather observations in the late 1800s and early 1900s could detect the movement and evolution of larger, synoptic scale, synoptic-scale systems like high pressure area, high and low-pressure area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Weather Prediction
Numerical weather prediction (NWP) uses mathematical models of the atmosphere and oceans to weather forecasting, predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic results. A number of global and regional forecast models are run in different countries worldwide, using current weather observations relayed from radiosondes, weather satellites and other observing systems as inputs. Mathematical models based on the same physical principles can be used to generate either short-term weather forecasts or longer-term climate predictions; the latter are widely applied for understanding and projecting climate change. The improvements made to regional models have allowed significant improvements in Tropical cyclone track forecasting, tropical cyclone track and air quality forecasts; however, atmospheric models perform poorly at han ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Land Surface
Terrain (), alternatively relief or topographical relief, is the dimension and shape of a given surface of land. In physical geography, terrain is the lay of the land. This is usually expressed in terms of the elevation, slope, and orientation of terrain features. Terrain affects surface water flow and distribution. Over a large area, it can affect weather and climate patterns. Bathymetry is the study of underwater relief, while hypsometry studies terrain relative to sea level. Importance The understanding of terrain is critical for many reasons: * The terrain of a region largely determines its suitability for human settlement: flatter alluvial plains tend to have better farming soils than steeper, rockier uplands. * In terms of environmental quality, agriculture, hydrology and other interdisciplinary sciences; understanding the terrain of an area assists the understanding of watershed boundaries, drainage characteristics, drainage systems, groundwater systems, wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematics
In physics, kinematics studies the geometrical aspects of motion of physical objects independent of forces that set them in motion. Constrained motion such as linked machine parts are also described as kinematics. Kinematics is concerned with systems of specification of objects' positions and velocities and mathematical transformations between such systems. These systems may be rectangular like Cartesian coordinate system, cartesian, Curvilinear coordinates like polar coordinates or other systems. The object trajectories may be specified with respect to other objects which may themselve be in motion relative to a standard reference. Rotating systems may also be used. Numerous practical problems in kinematics involve constraints, such as mechanical linkages, ropes, or rolling disks. Overview Kinematics is a subfield of physics and mathematics, developed in classical mechanics, that describes the motion of points, Physical object, bodies (objects), and systems of bodies (group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
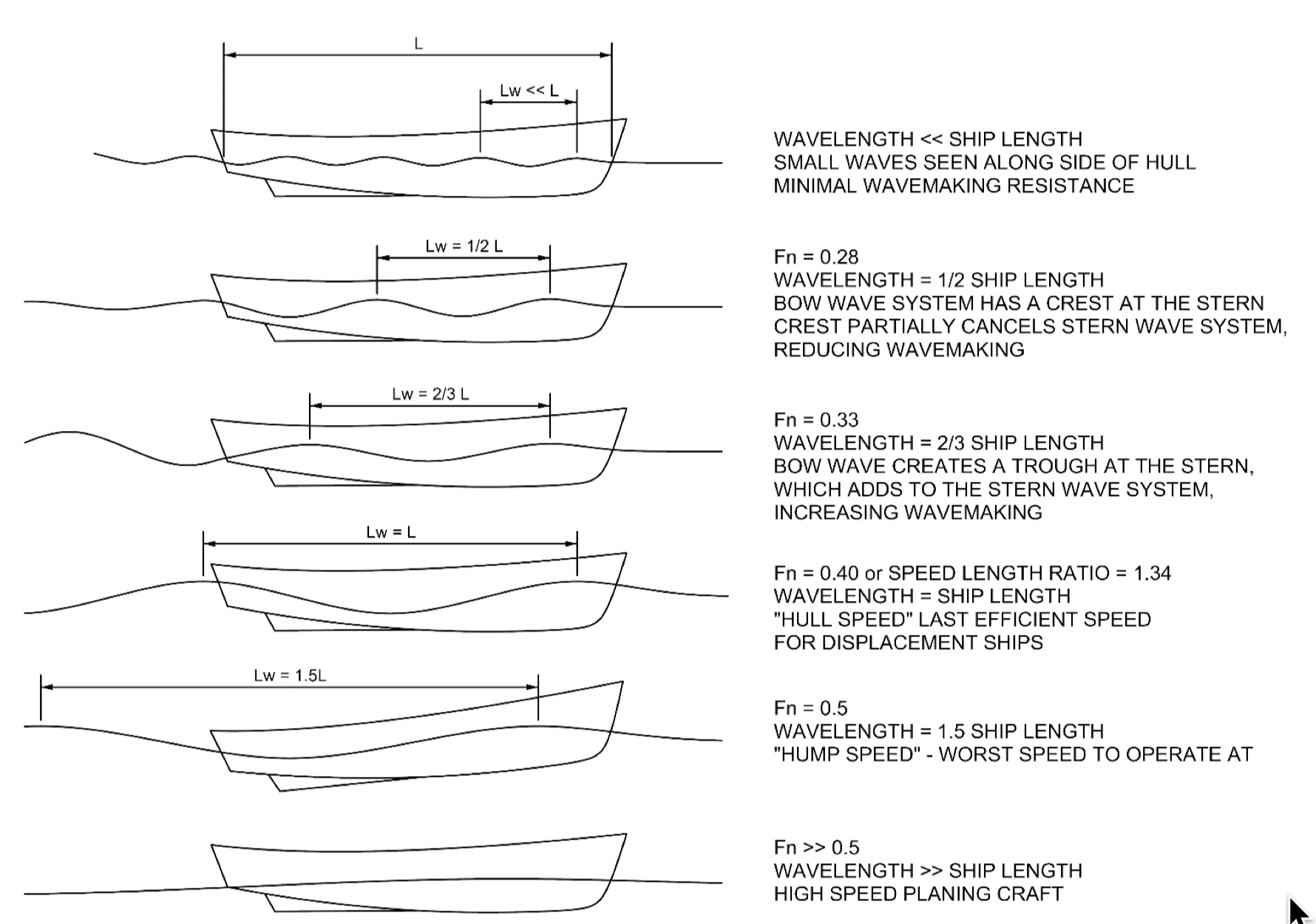
Froude Number
In continuum mechanics, the Froude number (, after William Froude, ) is a dimensionless number defined as the ratio of the flow inertia to the external force field (the latter in many applications simply due to gravity). The Froude number is based on the speed–length ratio which he defined as: \mathrm = \frac where is the local flow velocity (in m/s), is the local gravity field (in m/s2), and is a characteristic length (in m). The Froude number has some analogy with the Mach number. In theoretical fluid dynamics the Froude number is not frequently considered since usually the equations are considered in the high Froude limit of negligible external field, leading to homogeneous equations that preserve the mathematical aspects. For example, homogeneous Euler equations are conservation equations. However, in naval architecture the Froude number is a significant figure used to determine the resistance of a partially submerged object moving through water. Origins In open c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-step
A–K Apple Jacks A step on the spot, with twisting foot and the weight on the heel, likthis Ball change Ball change is a movement where the dancer shifts the weight from the ball of one foot to the other and back. This is mostly used in jazz and jive. Basic (step / figure / movement / or pattern) A basic figure is the very basic step that defines the character of a dance. Often it is called just thus: "basic movement", "basic step" or the like. For some dances it is sufficient to know the basic step performed in different handholds and dance positions to enjoy it socially. Body roll / body wave In this the dancer moves the body like a wave in standing position from head to legs, likthis Box step The box step is a dance figure named so because the steps rest in the four corners of a square. It is used, e.g., in American Style ballroom dances: rumba, waltz, bronze-level foxtrot. The leader begins with the left foot and proceeds as follows. :''First half-box'': ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |