|
Thomas Simpson
Thomas Simpson FRS (20 August 1710 – 14 May 1761) was a British mathematician and inventor known for the eponymous Simpson's rule to approximate definite integrals. The attribution, as often in mathematics, can be debated: this rule had been found 100 years earlier by Johannes Kepler, and in German it is called Keplersche Fassregel, or roughly "Kepler's Barrel Rule". Biography Simpson was born in Sutton Cheney, Leicestershire. The son of a weaver, Simpson taught himself mathematics. At the age of nineteen, he married a fifty-year old widow with two children. As a youth, he became interested in astrology after seeing a solar eclipse. He also dabbled in divination and caused fits in a girl after 'raising a devil' from her. After this incident, he and his wife fled to Derby. He moved with his wife and children to London at age twenty-five, where he supported his family by weaving during the day and teaching mathematics at night. From 1743, he taught mathematics at the Roy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sutton Cheney
Sutton Cheney ( ) is a village and former civil parish, now in the parish of Dadlington and Sutton Cheney, in the borough of Hinckley and Bosworth, in the county of Leicestershire, England, near the county border with Warwickshire.OS Explorer Map 232 : Nuneaton & Tamworth: (1:25 000) : In addition to the village of Sutton Cheney itself, the civil parish also contains the villages of Dadlington and Shenton, a number of farms, and the location of the Battle of Bosworth. Its closest large towns are Nuneaton and Hinckley. Its closest market town is Market Bosworth. The village of Sutton Cheney is clustered around the intersection of four roads: Ambion Lane leading westwards to the village of Shenton; Bosworth Road leading northwest to the neighbouring town of Market Bosworth; Main Street leading northeast to the villages of Cadeby, Leicestershire, Cadeby or Stapleton, Leicestershire, Stapleton; and Wharf Lane leading southwest to Sutton Cheney Wharf on the Ashby-de-la-Zouch Canal. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Royal Swedish Academy Of Sciences
The Royal Swedish Academy of Sciences () is one of the Swedish Royal Academies, royal academies of Sweden. Founded on 2 June 1739, it is an independent, non-governmental scientific organization that takes special responsibility for promoting natural sciences and mathematics and strengthening their influence in society, whilst endeavouring to promote the exchange of ideas between various disciplines. The goals of the academy are: * To be a forum where researchers meet across subject boundaries, * To offer a unique environment for research, * To provide support to younger researchers, * To reward outstanding research efforts, * To communicate internationally among scientists, * To advance the case for science within society and to influence research policy priorities * To stimulate interest in mathematics and science in school, and * To disseminate and popularize scientific information in various forms. Every year, the academy awards the Nobel Prizes in Nobel Prize in Physics, phy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
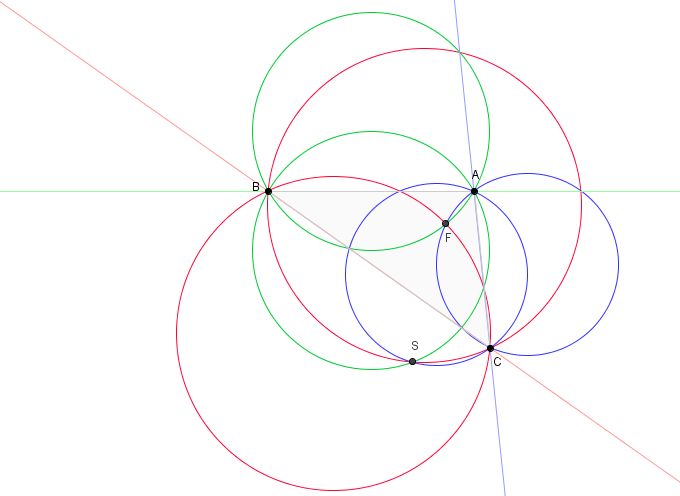
Fermat Point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible or, equivalently, the geometric median of the three vertices. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it. The Fermat point gives a solution to the geometric median and Steiner tree problems for three points. Construction The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows: # Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle. # Draw a line from each new vertex to the opposite vertex of the original triangle. # The two lines intersect at the Fermat point. An alternative method is the following: # On each of two ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Luc-Normand Tellier
Luc-Normand Tellier (born October 10, 1944) is a Professor Emeritus in spatial economics of the University of Quebec at Montreal. Education and teaching After teaching for two years (1964–1966) at the Collège Saint-André of Kigali, Rwanda, as a Canadian Peace Corps (CUSO/SUCO) volunteer, Tellier studied both economics and city planning. He obtained a bachelor's degree in Economics (1968) and a master's degree in City planning (1971) from the University of Montreal, as well as a master's degree (1971) and a Ph.D. (1973) in Regional science from the "Ivy League" University of Pennsylvania. Later, he taught urban economics at the "Institut d’urbanisme" of the University of Montreal before founding, in 1976, the Department of Urban Studies and Tourism of the University of Quebec at Montreal. He was chairman of that department for 13 years as well as, from 1981 to 1983, the director of the "Urbanisation" research center of the Institut National de la Recherche Scientifique (I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weber Problem
In geometry, the Weber problem, named after Alfred Weber, is one of the most famous problems in location theory. It requires finding a point in the plane that minimizes the sum of the transportation costs from this point to destination points, where different destination points are associated with different costs per unit distance. The Weber problem generalizes the geometric median, which assumes transportation costs per unit distance are the same for all destination points, and the problem of computing the Fermat point, the geometric median of three points. For this reason it is sometimes called the Fermat–Weber problem, although the same name has also been used for the unweighted geometric median problem. The Weber problem is in turn generalized by the attraction–repulsion problem, which allows some of the costs to be negative, so that greater distance from some points is better. Definition and history of the Fermat, Weber, and attraction-repulsion problems In the tri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alfred Weber
Carl David Alfred Weber (; 30 July 1868 – 2 May 1958) was a German economist, geographer, sociologist, philosopher, and theoretician of culture whose work was influential in the development of modern economic geography. His other work focused on the sociology of knowledge and the role of intellectuals in society. In particular, he introduced the concept of free-floating intelligentsia (''Freischwebende Intelligenz''). Life Alfred Weber, younger brother of the well-known sociologist Max Weber, was born in Erfurt and raised in Charlottenburg. From 1907 to 1933, he was a professor at Heidelberg University. Weber started his career as a lawyer and worked as a sociologist and cultural philosopher. Work Weber supported reintroducing theory and causal models to the field of economics, in addition to using historical analysis. In this field, his achievements involve work on early models of industrial location. He lived during the period when sociology became a separate fiel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marin Mersenne
Marin Mersenne, OM (also known as Marinus Mersennus or ''le Père'' Mersenne; ; 8 September 1588 – 1 September 1648) was a French polymath whose works touched a wide variety of fields. He is perhaps best known today among mathematicians for Mersenne prime numbers, those written in the form for some integer . He also developed Mersenne's laws, which describe the harmonics of a vibrating string (such as may be found on guitars and pianos), and his seminal work on music theory, '' Harmonie universelle'', for which he is referred to as the "father of acoustics". Mersenne, an ordained Catholic priest, had many contacts in the scientific world and has been called "the center of the world of science and mathematics during the first half of the 1600s" and, because of his ability to make connections between people and ideas, "the post-box of Europe". He was also a member of the ascetical Minim religious order and wrote and lectured on theology and philosophy. Life Mersenne was b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pierre De Fermat
Pierre de Fermat (; ; 17 August 1601 – 12 January 1665) was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he is recognized for his discovery of an original method of finding the greatest and the smallest ordinates of curved lines, which is analogous to that of differential calculus, then unknown, and his research into number theory. He made notable contributions to analytic geometry, probability, and optics. He is best known for his Fermat's principle for light propagation and his Fermat's Last Theorem in number theory, which he described in a note at the margin of a copy of Diophantus' ''Arithmetica''. He was also a lawyer at the ''parlement'' of Toulouse, France. Biography Fermat was born in 1601 in Beaumont-de-Lomagne, France—the late 15th-century mansion where Fermat was born is now a museum. He was from Gascony, where his father, Dominique Fermat, was a wealthy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramount to his method of inquiry, and he connected the previously separate fields of geometry and algebra into analytic geometry. Descartes spent much of his working life in the Dutch Republic, initially serving the Dutch States Army, and later becoming a central intellectual of the Dutch Golden Age. Although he served a Dutch Reformed Church, Protestant state and was later counted as a Deism, deist by critics, Descartes was Roman Catholicism, Roman Catholic. Many elements of Descartes's philosophy have precedents in late Aristotelianism, the Neostoicism, revived Stoicism of the 16th century, or in earlier philosophers like Augustine of Hippo, Augustine. In his natural philosophy, he differed from the Scholasticism, schools on two major point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Gregory (astronomer And Mathematician)
James Gregory (November 1638 – October 1675) was a Scottish mathematician and astronomer. His surname is sometimes spelt as Gregorie, the original Scottish spelling. He described an early practical design for the reflecting telescope – the Gregorian telescope – and made advances in trigonometry, discovering infinite series representations for several trigonometric functions. In his book ''Geometriae Pars Universalis'' (1668) Gregory gave both the first published statement and proof of the fundamental theorem of the calculus (stated from a geometric point of view, and only for a special class of the curves considered by later versions of the theorem), for which he was acknowledged by Isaac Barrow. Biography Gregory was born in 1638. His mother Janet was the daughter of Jean and David Anderson and his father was John Gregory, an Episcopalian Church of Scotland minister, James was youngest of their three children and he was born in the manse at Drumoak, Aberdeenshire, and wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bonaventura Cavalieri
Bonaventura Francesco Cavalieri (; 1598 – 30 November 1647) was an Italian mathematician and a Jesuati, Jesuate. He is known for his work on the problems of optics and motion (physics), motion, work on indivisibles, the precursors of infinitesimal calculus, and the introduction of logarithms to Italy. Cavalieri's principle in geometry partially anticipated integral calculus. Life Born in Milan, Cavalieri joined the Jesuates order (not to be confused with the Society of Jesus, Jesuits) at the age of fifteen, taking the name Bonaventura upon becoming a novice of the order, and remained a member until his death. He took his vows as a full member of the order in 1615, at the age of seventeen, and shortly after joined the Jesuat house in Pisa. By 1616 he was a student of geometry at the University of Pisa. There he came under the tutelage of Benedetto Castelli, who probably introduced him to Galileo Galilei. In 1617 he briefly joined the House of Medici, Medici court in Floren ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simpson's Rule
In numerical integration, Simpson's rules are several approximations for definite integrals, named after Thomas Simpson (1710–1761). The most basic of these rules, called Simpson's 1/3 rule, or just Simpson's rule, reads \int_a^b f(x) \, dx \approx \frac \left (a) + 4f\left(\frac\right) + f(b)\right In German and some other languages, it is named after Johannes Kepler, who derived it in 1615 after seeing it used for wine barrels (barrel rule, ). The approximate equality in the rule becomes exact if is a polynomial up to and including 3rd degree. If the 1/3 rule is applied to ''n'' equal subdivisions of the integration range 'a'', ''b'' one obtains the composite Simpson's 1/3 rule. Points inside the integration range are given alternating weights 4/3 and 2/3. Simpson's 3/8 rule, also called Simpson's second rule, requires one more function evaluation inside the integration range and gives lower error bounds, but does not improve the order of the error. If the 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |