|
Tensorsketch
In statistics, machine learning and algorithms, a tensor sketch is a type of dimensionality reduction that is particularly efficient when applied to vectors that have tensor structure. Such a sketch can be used to speed up explicit kernel methods, bilinear pooling in neural networks and is a cornerstone in many numerical linear algebra algorithms.Woodruff, David P.Sketching as a Tool for Numerical Linear Algebra." Theoretical Computer Science 10.1-2 (2014): 1–157. Mathematical definition Mathematically, a dimensionality reduction or sketching matrix is a matrix M\in\mathbb R^, where k |
Count Sketch
Count sketch is a type of dimensionality reduction that is particularly efficient in statistics, machine learning and algorithms. It was invented by Moses Charikar, Kevin Chen and Martin Farach-Colton in an effort to speed up the AMS Sketch by Alon, Matias and Szegedy for approximating the frequency moments of streams. The sketch is nearly identical to the Feature hashing algorithm by John Moody, but differs in its use of hash functions with low dependence, which makes it more practical. In order to still have a high probability of success, the median trick is used to aggregate multiple count sketches, rather than the mean. These properties allow use for explicit kernel methods, bilinear pooling in neural networks and is a cornerstone in many numerical linear algebra algorithms.Woodruff, David P. "Sketching as a Tool for Numerical Linear Algebra." Theoretical Computer Science 10.1-2 (2014): 1–157. Mathematical definition 1. For constants w and t (to be defined later) ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result (see commutativity). The integral is evaluated for all values of shift, producing the convolution function. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution (f*g) differs from cross-correlation (f \star g) only in that either or is reflected about the y-axis in convolution; thus it is a cross-correlation of and , or and . For complex-valued fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernard Chazelle
Bernard Chazelle (born November 5, 1955) is a French-American computer scientist. He is currently the Eugene Higgins Professor of Computer Science at Princeton University. Much of his work is in computational geometry, where he is known for his study of algorithms, such as linear-time triangulation of a simple polygon, as well as major complexity results, such as lower bound techniques based on discrepancy theory. He is also known for his invention of the soft heap data structure and the most asymptotically efficient known algorithm for finding minimum spanning trees. Early life Chazelle was born in Clamart, France, the son of Marie-Claire (née Blanc) and Jean Chazelle. He grew up in Paris, France, where he received his bachelor's degree and master's degree in applied mathematics at the École des mines de Paris in 1977. Then, at the age of 21, he attended Yale University in the United States, where he received his PhD in computer science in 1980 under the supervision of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson–Lindenstrauss Lemma
In mathematics, the Johnson–Lindenstrauss lemma is a result named after William B. Johnson and Joram Lindenstrauss concerning low-distortion embeddings of points from high-dimensional into low-dimensional Euclidean space. The lemma states that a set of points in a high-dimensional space can be embedded into a space of much lower dimension in such a way that distances between the points are nearly preserved. The map used for the embedding is at least Lipschitz, and can even be taken to be an orthogonal projection. The lemma has applications in compressed sensing, manifold learning, dimensionality reduction, and graph embedding. Much of the data stored and manipulated on computers, including text and images, can be represented as points in a high-dimensional space (see vector space model for the case of text). However, the essential algorithms for working with such data tend to become bogged down very quickly as dimension increases. It is therefore desirable to reduce the dimens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthonormal
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal (or perpendicular along a line) unit vectors. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length. An orthonormal set which forms a basis is called an orthonormal basis. Intuitive overview The construction of orthogonality of vectors is motivated by a desire to extend the intuitive notion of perpendicular vectors to higher-dimensional spaces. In the Cartesian plane, two vectors are said to be ''perpendicular'' if the angle between them is 90° (i.e. if they form a right angle). This definition can be formalized in Cartesian space by defining the dot product and specifying that two vectors in the plane are orthogonal if their dot product is zero. Similarly, the construction of the norm of a vector is motivated by a desire to extend the intuitive notion of the length of a vector to higher-dimensional spaces. In Cartes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
DFT Matrix
In applied mathematics, a DFT matrix is an expression of a discrete Fourier transform (DFT) as a transformation matrix, which can be applied to a signal through matrix multiplication. Definition An ''N''-point DFT is expressed as the multiplication X = W x, where x is the original input signal, W is the ''N''-by-''N'' square DFT matrix, and X is the DFT of the signal. The transformation matrix W can be defined as W = \left(\frac\right)_ , or equivalently: : W = \frac \begin 1&1&1&1&\cdots &1 \\ 1&\omega&\omega^2&\omega^3&\cdots&\omega^ \\ 1&\omega^2&\omega^4&\omega^6&\cdots&\omega^\\ 1&\omega^3&\omega^6&\omega^9&\cdots&\omega^\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ 1&\omega^&\omega^&\omega^&\cdots&\omega^ \end , where \omega = e^ is a primitive ''N''th root of unity in which i^2=-1. We can avoid writing large exponents for \omega using the fact that for any exponent x we have the identity \omega^ = \omega^. This is the Vandermonde matrix for the roots of unity, up to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Antenna Array
Digital antenna array (DAA) is a smart antenna with multi channels digital beamforming, usually by using fast Fourier transform (FFT). The development and practical realization of digital antenna arrays theory started in 1962 under the guidance of Vladimir Varyukhin (USSR). History The history of the DAA was started to emerge as a theory of multichannel analysis in the 1920s.Slyusar V. I. Origins of the Digital Antenna Array Theory.// International Conference on Antenna Theory and Techniques, 24–27 May 2017, Kyiv, Ukraine. – Pp. 199 - 20/ref> In the 1940s this theory evolved to the theory of three-channel antenna analyzers. The implementation of effective signal processing in radars by the end of the 1950s predetermined the use of electronic computers in this field. In 1957, Ben S. Meltont and Leslie F. Bailey published article regarding using algebraic operations for signal processing with the help of electronic circuits or analog computer. Three years after in 1960 th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radar
Radar is a detection system that uses radio waves to determine the distance ('' ranging''), angle, and radial velocity of objects relative to the site. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. A radar system consists of a transmitter producing electromagnetic waves in the radio or microwaves domain, a transmitting antenna, a receiving antenna (often the same antenna is used for transmitting and receiving) and a receiver and processor to determine properties of the objects. Radio waves (pulsed or continuous) from the transmitter reflect off the objects and return to the receiver, giving information about the objects' locations and speeds. Radar was developed secretly for military use by several countries in the period before and during World War II. A key development was the cavity magnetron in the United Kingdom, which allowed the creation of relatively small systems with sub-meter resolution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
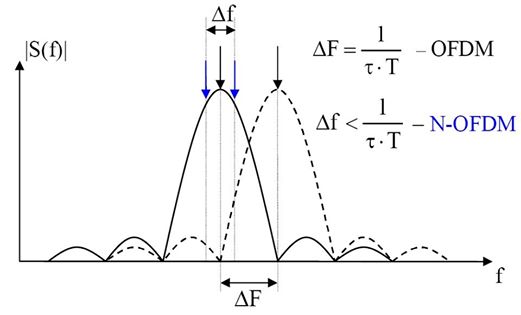
Vadym Slyusar
Vadym Slyusar (born 15 October 1964, vil. Kolotii, Reshetylivka Raion, Poltava region, Ukraine) – Soviet and Ukrainian scientist, Professor, Doctor of Technical Sciences, Honored Scientist and Technician of Ukraine, founder of tensor-matrix theory of digital antenna arrays (DAAs), N-OFDM and other theories in fields of radar systems, smart antennas for wireless communications and digital beamforming. Scientific results N-OFDM theory In 1992 Vadym Slyusar patented the 1st optimal demodulation method for N-OFDM signals after Fast Fourier transform (FFT).RU2054684 (C1) G01R 23/16. Amplitude-frequency response measurement technique// Slyusar V. – Appl. Number SU 19925055759, Priority Data: 19920722. – Official Publication Data: 1996-02-2/ref> From this patent was started the history of N-OFDM signals theory. In this regard, W. Kozek and A. F. Molisch wrote in 1998 about N-OFDM signals with the sub-carrier spacing \alpha before the conference paper of I. Darwazeh and M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Khatri–Rao Product
In mathematics, the Khatri–Rao product of matrices defined as : \mathbf \ast \mathbf = \left(\mathbf_ \otimes \mathbf_\right)_ in which the ''ij''-th block is the sized Kronecker product of the corresponding blocks of A and B, assuming the number of row and column partitions of both matrices is equal. The size of the product is then . For example, if A and B both are partitioned matrices e.g.: : \mathbf = \left \begin \mathbf_ & \mathbf_ \\ \hline \mathbf_ & \mathbf_ \end \right= \left \begin 1 & 2 & 3 \\ 4 & 5 & 6 \\ \hline 7 & 8 & 9 \end \right,\quad \mathbf = \left \begin \mathbf_ & \mathbf_ \\ \hline \mathbf_ & \mathbf_ \end \right= \left \begin 1 & 4 & 7 \\ \hline 2 & 5 & 8 \\ 3 & 6 & 9 \end \right, we obtain: : \mathbf \ast \mathbf = \left \begin \mathbf_ \otimes \mathbf_ & \mathbf_ \otimes \mathbf_ \\ \hline \mathbf_ \otimes \mathbf_ & \mathbf_ \otimes \mathbf_ \end \right= \left \begin 1 & 2 & 12 & 21 \\ 4 & 5 & 24 & 42 \\ \hline 14 & 16 & 45 & 72 \\ 21 & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |