|
Tau-equivalent Reliability
Cronbach's alpha (Cronbach's \alpha), also known as tau-equivalent reliability (\rho_T) or coefficient alpha (coefficient \alpha), is a reliability coefficient that provides a method of measuring internal consistency of tests and measures. Numerous studies warn against using it unconditionally, and note that reliability coefficients based on structural equation modeling (SEM) are in many cases a suitable alternative.Sijtsma, K. (2009). On the use, the misuse, and the very limited usefulness of Cronbach's alpha. Psychometrika, 74(1), 107–120. Green, S. B., & Yang, Y. (2009). Commentary on coefficient alpha: A cautionary tale. Psychometrika, 74(1), 121–135. Revelle, W., & Zinbarg, R. E. (2009). Coefficients alpha, beta, omega, and the glb: Comments on Sijtsma. Psychometrika, 74(1), 145–154. Cho, E., & Kim, S. (2015). Cronbach's coefficient alpha: Well known but poorly understood. Organizational Research Methods, 18(2), 207–230. Raykov, T., & Marcoulides, G. A. (2017). Thanks ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reliability Coefficient
In statistics and psychometrics, reliability is the overall consistency of a measure. A measure is said to have a high reliability if it produces similar results under consistent conditions:"It is the characteristic of a set of test scores that relates to the amount of random error from the measurement process that might be embedded in the scores. Scores that are highly reliable are precise, reproducible, and consistent from one testing occasion to another. That is, if the testing process were repeated with a group of test takers, essentially the same results would be obtained. Various kinds of reliability coefficients, with values ranging between 0.00 (much error) and 1.00 (no error), are usually used to indicate the amount of error in the scores." For example, measurements of people's height and weight are often extremely reliable.The Marketing Accountability Standards Board (MASB) endorses this definition as part of its ongoinCommon Language: Marketing Activities and Metrics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Consistency
In statistics and research, internal consistency is typically a measure based on the correlations between different items on the same test (or the same subscale on a larger test). It measures whether several items that propose to measure the same general construct produce similar scores. For example, if a respondent expressed agreement with the statements "I like to ride bicycles" and "I've enjoyed riding bicycles in the past", and disagreement with the statement "I hate bicycles", this would be indicative of good internal consistency of the test. Cronbach's alpha Internal consistency is usually measured with Cronbach's alpha, a statistic calculated from the pairwise correlations between items. Internal consistency ranges between negative infinity and one. Coefficient alpha will be negative whenever there is greater within-subject variability than between-subject variability. A commonly accepted rule of thumb for describing internal consistency is as follows: Very high reliabi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Equation Modeling
Structural equation modeling (SEM) is a label for a diverse set of methods used by scientists in both experimental and observational research across the sciences, business, and other fields. It is used most in the social and behavioral sciences. A definition of SEM is difficult without reference to highly technical language, but a good starting place is the name itself. SEM involves the construction of a '' model'', to represent how various aspects of an observable or theoretical phenomenon are thought to be causally structurally related to one another. The ''structural'' aspect of the model implies theoretical associations between variables that represent the phenomenon under investigation. The postulated causal structuring is often depicted with arrows representing causal connections between variables (as in Figures 1 and 2) but these causal connections can be equivalently represented as equations. The causal structures imply that specific patterns of connections should app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Current Contents
''Current Contents'' is a rapid alerting service database from Clarivate Analytics, formerly the Institute for Scientific Information and Thomson Reuters. It is published online and in several different printed subject sections. History ''Current Contents'' was first published in paper format, in a single edition devoted only to biology and medicine. Other subject editions were added later. Initially, it consisted simply of a reproduction of the title pages from several hundred major peer-reviewed scientific journals, and was published weekly, with the issues containing title pages from journal issues only a few weeks previously, a shorter time lag than any service then available. There was an author index and a crude keyword subject index only. Author addresses were provided so readers could send reprint requests for copies of the actual articles. Status Still published in print, it is available as one of the databases included in Clarivate Analytics' ISI Web of Knowledge w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearity
Linearity is the property of a mathematical relationship ('' function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear relationship of voltage and current in an electrical conductor (Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships are ''nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. The word linear comes from Latin ''linearis'', "pertaining to or resembling a line". In mathematics In mathematics, a linear map or linear function ''f''(''x'') is a function that satisfies the two properties: * Additivity: . * Homogeneity of degree 1: for all α. These properties are known as the superposition principle. In this definition, ''x'' is not necessarily a r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independence (statistics)
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independence, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Congeneric Reliability
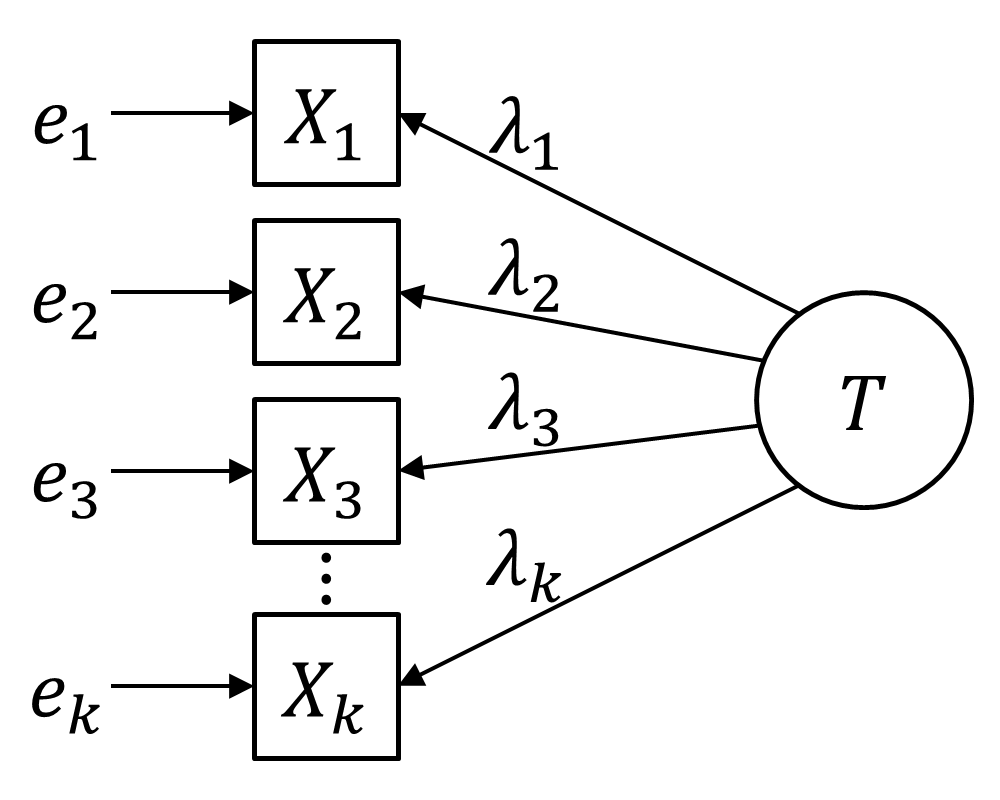
In statistical models applied to psychometrics, congeneric reliability \rho_C ("rho C")Cho, E. (2016). Making reliability reliable: A systematic approach to reliability coefficients. Organizational Research Methods, 19(4), 651–682. https://doi.org/10.1177/1094428116656239 a single-administration test score reliability (i.e., the reliability of persons over items holding occasion fixed coefficient, commonly referred to as composite reliability, construct reliability, and coefficient omega. \rho_C is a structural equation model(SEM)-based reliability coefficients and is obtained from on a unidimensional model. \rho_C is the second most commonly used reliability factor after tau-equivalent reliability(\rho_T), and is often recommended as its alternative. Formula and calculation Systematic and conventional formula Let X_i denote the observed score of item i and X(=X_1 + X_2 + \cdots + X_k) denote the sum of all items in a test consisting of k items. It is assumed that each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Of Assessments
Comparison or comparing is the act of evaluating two or more things by determining the relevant, comparable characteristics of each thing, and then determining which characteristics of each are similar to the other, which are different, and to what degree. Where characteristics are different, the differences may then be evaluated to determine which thing is best suited for a particular purpose. The description of similarities and differences found between the two things is also called a comparison. Comparison can take many distinct forms, varying by field: To compare things, they must have characteristics that are similar enough in relevant ways to merit comparison. If two things are too different to compare in a useful way, an attempt to compare them is colloquially referred to in English as "comparing apples and oranges." Comparison is widely used in society, in science and in the arts. General usage Comparison is a natural activity, which even animals engage in when deci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Reliability
In statistics, a consistent estimator or asymptotically consistent estimator is an estimator—a rule for computing estimates of a parameter ''θ''0—having the property that as the number of data points used increases indefinitely, the resulting sequence of estimates converges in probability to ''θ''0. This means that the distributions of the estimates become more and more concentrated near the true value of the parameter being estimated, so that the probability of the estimator being arbitrarily close to ''θ''0 converges to one. In practice one constructs an estimator as a function of an available sample of size ''n'', and then imagines being able to keep collecting data and expanding the sample ''ad infinitum''. In this way one would obtain a sequence of estimates indexed by ''n'', and consistency is a property of what occurs as the sample size “grows to infinity”. If the sequence of estimates can be mathematically shown to converge in probability to the true value ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |