|
System Of Differential Equations
In mathematics, a system of differential equations is a finite set of differential equations. Such a system can be either linear or non-linear. Also, such a system can be either a system of ordinary differential equations or a system of partial differential equations. Linear systems of differential equations A first-order linear system of ODEs is a system in which every equation is first order and depends on the unknown functions linearly. Here we consider systems with an equal number of unknown functions and equations. These may be written as \frac = a_(t) x_1 + \ldots + a_(t)x_n + g_(t), \qquad j=1,\ldots,n where n is a positive integer, and a_(t),g_(t) are arbitrary functions of the independent variable t. A first-order linear system of ODEs may be written in matrix form: \frac \begin x_1 \\ x_2 \\ \vdots \\ x_n \end = \begin a_ & \ldots & a_ \\ a_ & \ldots & a_ \\ \vdots & \ldots & \vdots \\ a_ & & a_ \end \begin x_1 \\ x_2 \\ \vdots \\ x_n \end + \begin g_1 \\ g_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions that are given on a hypersurface in the domain. A Cauchy problem can be an initial value problem or a boundary value problem (for this case see also Cauchy boundary condition). It is named after Augustin-Louis Cauchy. Formal statement For a partial differential equation defined on R''n+1'' and a smooth manifold ''S'' ⊂ R''n+1'' of dimension ''n'' (''S'' is called the Cauchy surface), the Cauchy problem consists of finding the unknown functions u_1,\dots,u_N of the differential equation with respect to the independent variables t,x_1,\dots,x_n that satisfies \begin&\frac = F_i\left(t,x_1,\dots,x_n,u_1,\dots,u_N,\dots,\frac,\dots\right) \\ &\text i,j = 1,2,\dots,N;\, k_0+k_1+\dots+k_n=k\leq n_j;\, k_0 |
Cartan–Kuranishi Prolongation Theorem
Given an exterior differential system defined on a manifold ''M'', the Cartan–Kuranishi prolongation theorem says that after a finite number of ''prolongations'' the system is either ''in involution'' (admits at least one 'large' integral manifold), or is impossible. History The theorem is named after Élie Cartan and Masatake Kuranishi. Cartan made several attempts in 1946 to prove the result, but it was in 1957 that Kuranishi provided a proof of Cartan's conjecture. Applications This theorem is used in infinite-dimensional Lie theory In mathematics, the mathematician Sophus Lie ( ) initiated lines of study involving integration of differential equations, transformation groups, and contact (mathematics), contact of spheres that have come to be called Lie theory. For instance, .... See also * Cartan-Kähler theorem References * M. Kuranishi, ''On É. Cartan's prolongation theorem of exterior differential systems'', Amer. J. Math., vol. 79, 1957, p. 1–47 * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Geometry
In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant (or equivariant) transformations from the space of functions on one geometrical space to the space of functions on another geometrical space. Such transformations often take the form of integral transforms such as the Radon transform and its generalizations. Classical context Integral geometry as such first emerged as an attempt to refine certain statements of geometric probability theory. The early work of Luis Santaló and Wilhelm Blaschke was in this connection. It follows from the classic theorem of Crofton expressing the length of a plane curve as an expectation of the number of intersections with a random line. Here the word 'random' must be interpreted as subject to correct symmetry considerations. There is a sample space of lines, one on which the a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrability Conditions For Differential Systems
In mathematics, certain systems of partial differential equations are usefully formulated, from the point of view of their underlying geometric and algebraic structure, in terms of a system of differential forms. The idea is to take advantage of the way a differential form ''restricts'' to a submanifold, and the fact that this restriction is compatible with the exterior derivative. This is one possible approach to certain over-determined systems, for example, including Lax pairs of integrable systems. A Pfaffian system is specified by 1-forms alone, but the theory includes other types of example of differential system. To elaborate, a Pfaffian system is a set of 1-forms on a smooth manifold (which one sets equal to 0 to find ''solutions'' to the system). Given a collection of differential 1-forms \textstyle\alpha_i, i=1,2,\dots, k on an \textstyle n-dimensional manifold , an integral manifold is an immersed (not necessarily embedded) submanifold whose tangent space at every poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
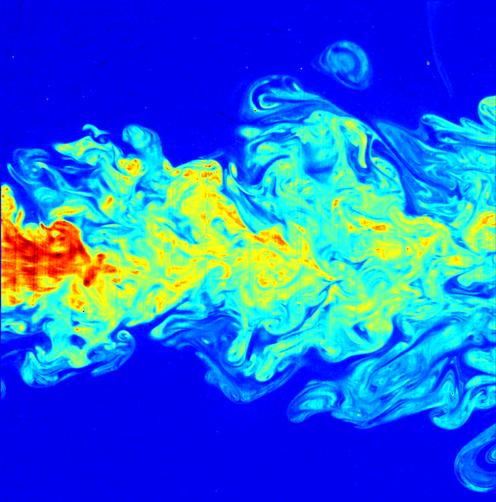
Navier–Stokes Existence And Smoothness
The Navier–Stokes existence and smoothness problem concerns the mathematical properties of solutions to the Navier–Stokes equations, a system of partial differential equations that describe the motion of a fluid in space. Solutions to the Navier–Stokes equations are used in many practical applications. However, theoretical understanding of the solutions to these equations is incomplete. In particular, solutions of the Navier–Stokes equations often include turbulence, which remains one of the greatest unsolved problems in physics, despite its immense importance in science and engineering. Even more basic (and seemingly intuitive) properties of the solutions to Navier–Stokes have never been proven. For the three-dimensional system of equations, and given some initial conditions, mathematicians have neither proved that smooth solutions always exist, nor found any counter-examples. This is called the ''Navier–Stokes existence and smoothness'' problem. Since underst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Navier–Stokes Equations
The Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes). The Navier–Stokes equations mathematically express momentum balance for Newtonian fluids and make use of conservation of mass. They are sometimes accompanied by an equation of state relating pressure, temperature and density. They arise from applying Isaac Newton's second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscous term (proportional to the gradient of velocity) and a pressure term—hence describing ''viscous flow''. The difference between them and the closely related Euler equations is that Navier–Stokes equat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ehrenpreis's Fundamental Principle
In mathematical analysis, Ehrenpreis's fundamental principle, introduced by Leon Ehrenpreis, states: :Every solution of a system (in general, overdetermined) of homogeneous partial differential equations with constant coefficient In mathematics, a coefficient is a Factor (arithmetic), multiplicative factor involved in some Summand, term of a polynomial, a series (mathematics), series, or any other type of expression (mathematics), expression. It may be a Dimensionless qu ...s can be represented as the integral with respect to an appropriate Radon measure over the complex “ characteristic variety” of the system. References Mathematical analysis {{analysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compatibility Conditions
Compatibility may refer to: Computing * Backward compatibility, in which newer systems can understand data generated by older ones * Compatibility card, an expansion card for hardware emulation of another device * Compatibility layer, components that allow for non-native support of components ** Compatibility mode, software mechanism in which a software emulates an older version of software * Computer compatibility, of a line of machines ** IBM PC compatible, computers that are generally similar to the original IBM PC, XT, or AT * Forward compatibility, in which older systems can understand data generated by newer ones * Hardware compatibility, between different pieces of computer hardware * License compatibility, of software licenses * Pin compatibility, in devices that have the same functions assigned to the same particular pins * Software compatibility, between different pieces of software ** Software incompatibility Science and mathematics * Biocompatibility, a description o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Differential Equations
In mathematics, a linear differential equation is a differential equation that is linear in the unknown function and its derivatives, so it can be written in the form a_0(x)y + a_1(x)y' + a_2(x)y'' \cdots + a_n(x)y^ = b(x) where and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of an unknown function of the variable . Such an equation is an ordinary differential equation (ODE). A ''linear differential equation'' may also be a linear partial differential equation (PDE), if the unknown function depends on several variables, and the derivatives that appear in the equation are partial derivatives. Types of solution A linear differential equation or a system of linear equations such that the associated homogeneous equations have constant coefficients may be solved by quadrature, which means that the solutions may be expressed in terms of integrals. This is also true for a linear equation of order one, with non-constant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |