Superstatistics
Superstatistics is a branch of statistical mechanics or statistical physics devoted to the study of non-linear and non-equilibrium systems. It is characterized by using the superposition of multiple differing statistical models to achieve the desired non-linearity. In terms of ordinary statistical ideas, this is equivalent to compounding the distributions of random variables and it may be considered a simple case of a doubly stochastic model. Consider an extended thermodynamical system which is locally in equilibrium and has a Boltzmann distribution, that is the probability of finding the system in a state with energy E is proportional to \exp(-\beta E). Here \beta is the local inverse temperature. A non-equilibrium thermodynamical system is modeled by considering macroscopic fluctuations of the local inverse temperature. These fluctuations happen on time scales which are much larger than the microscopic relaxation times to the Boltzmann distribution. If the fluctuations of \beta ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Physica A
Physica may refer to: * Physics (Aristotle) * ''Physica'', a twelfth-century medical text by Hildegard of Bingen * ''Physica'' (journal), a Dutch scientific journal :* ''Physica A'' :* ''Physica B'' ;* ''Physica C'' :* ''Physica D'' :* ''Physica E'' * ''Physica Scripta ''Physica Scripta'' is an international scientific journal for experimental and theoretical physics. It was established in 1970 as the successor of ''Arkiv för Fysik'' and published by the Royal Swedish Academy of Sciences (KVA). Since 2006, it ha ...

Proceedings Of The National Academy Of Sciences
''Proceedings of the National Academy of Sciences of the United States of America'' (often abbreviated ''PNAS'' or ''PNAS USA'') is a peer-reviewed multidisciplinary scientific journal. It is the official journal of the National Academy of Sciences, published since 1915, and publishes original research, scientific reviews, commentaries, and letters. According to ''Journal Citation Reports'', the journal has a 2022 impact factor of 9.4. ''PNAS'' is the second most cited scientific journal, with more than 1.9 million cumulative citations from 2008 to 2018. In the past, ''PNAS'' has been described variously as "prestigious", "sedate", "renowned" and "high impact". ''PNAS'' is a delayed open-access journal, with an embargo period of six months that can be bypassed for an author fee ( hybrid open access). Since September 2017, open access articles are published under a Creative Commons license. Since January 2019, ''PNAS'' has been online-only, although print issues are available ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Maxwell–Boltzmann Statistics
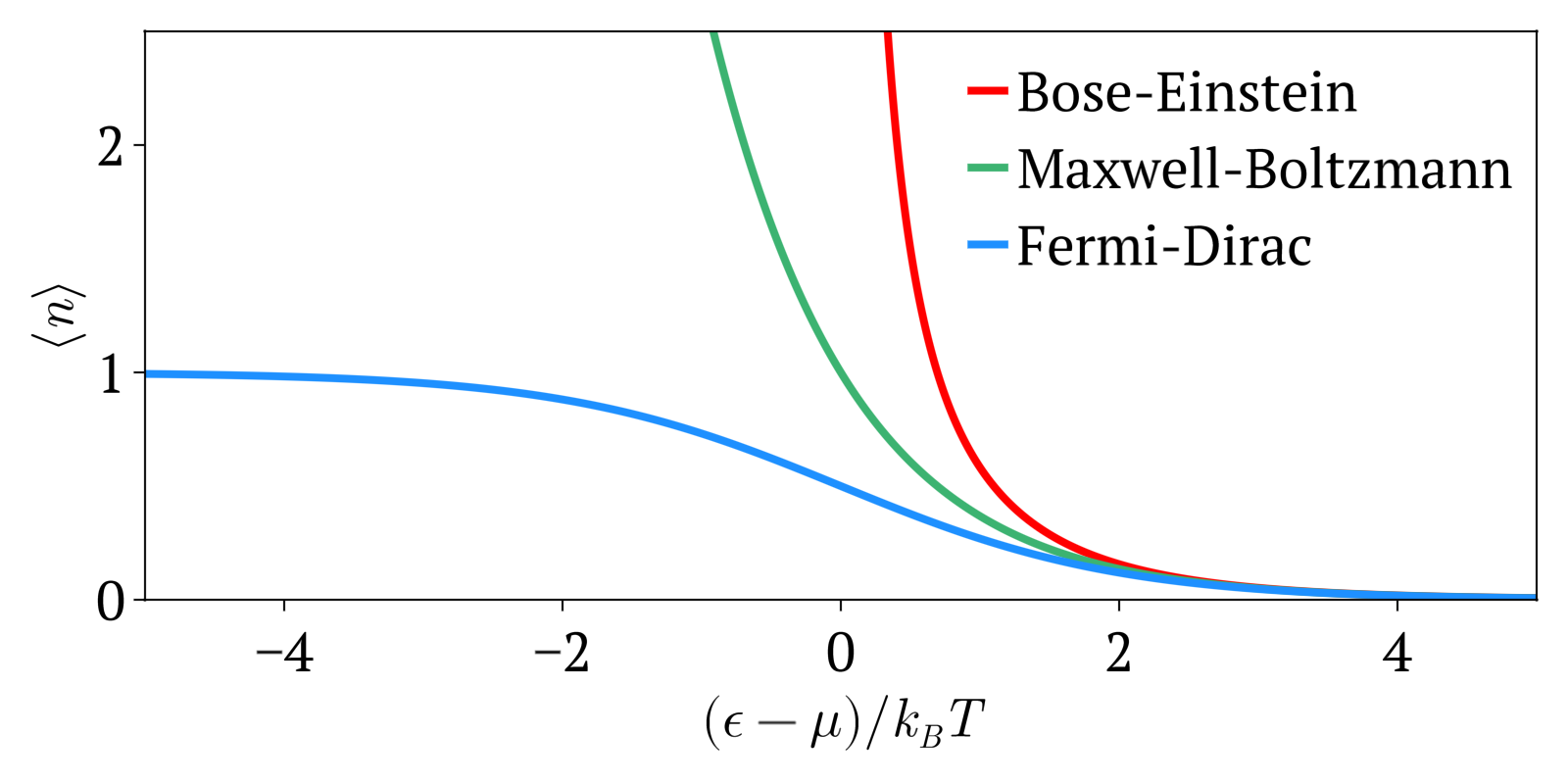
In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density is low enough to render quantum effects negligible. The expected number of particles with energy \varepsilon_i for Maxwell–Boltzmann statistics is : \langle N_i \rangle = \frac = \frac\,g_i e^, where: * \varepsilon_i is the energy of the ''i''th energy level, * \langle N_i \rangle is the average number of particles in the set of states with energy \varepsilon_i, * g_i is the degeneracy of energy level ''i'', that is, the number of states with energy \varepsilon_i which may nevertheless be distinguished from each other by some other means,For example, two simple point particles may have the same energy, but different momentum vectors. They may be distinguished from each other on this basis, and the degeneracy will be the number of po ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Mixing (mathematics)
In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: e.g. mixing paint, mixing drinks, industrial mixing. The concept appears in ergodic theory—the study of stochastic processes and measure-preserving dynamical systems. Several different definitions for mixing exist, including ''strong mixing'', ''weak mixing'' and ''topological mixing'', with the last not requiring a measure to be defined. Some of the different definitions of mixing can be arranged in a hierarchical order; thus, strong mixing implies weak mixing. Furthermore, weak mixing (and thus also strong mixing) implies ergodicity: that is, every system that is weakly mixing is also ergodic (and so one says that mixing is a "stronger" condition than ergodicity). Informal explanation The mathematical definition of mixing aims to capture the ordinary every-day process of mixing, such as mixing paints, dri ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Exponential Family
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, including the enabling of the user to calculate expectations, covariances using differentiation based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. Sometimes loosely referred to as ''the'' exponential family, this class of distributions is distinct because they all possess a variety of desirable properties, most importantly the existence of a sufficient statistic. The concept of exponential families is credited to E. J. G. Pitman, G. Darmois, and B. O. Koopman in 1935–1936. Exponential families of distributions provide a general framework for selecting ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Boltzmann Distribution
In statistical mechanics and mathematics, a Boltzmann distribution (also called Gibbs distribution Translated by J.B. Sykes and M.J. Kearsley. See section 28) is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. The distribution is expressed in the form: :p_i \propto \exp\left(- \frac \right) where is the probability of the system being in state , is the exponential function, is the energy of that state, and a constant of the distribution is the product of the Boltzmann constant and thermodynamic temperature . The symbol \propto denotes proportionality (see for the proportionality constant). The term ''system'' here has a wide meaning; it can range from a collection of 'sufficient number' of atoms or a single atom to a macroscopic system such as a natural gas storage tank. Therefore, the Boltzmann distribution can be used to sol ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Thermodynamic Equilibrium
Thermodynamic equilibrium is a notion of thermodynamics with axiomatic status referring to an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable walls. In thermodynamic equilibrium, there are no net macroscopic flows of mass nor of energy within a system or between systems. In a system that is in its own state of internal thermodynamic equilibrium, not only is there an absence of macroscopic change, but there is an “absence of any ''tendency'' toward change on a macroscopic scale.” Systems in mutual thermodynamic equilibrium are simultaneously in mutual thermal, mechanical, chemical, and radiative equilibria. Systems can be in one kind of mutual equilibrium, while not in others. In thermodynamic equilibrium, all kinds of equilibrium hold at once and indefinitely, unless disturbed by a thermodynamic operation. In a macroscopic equilibrium, perfectly or almost perfectly ba ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Physica D
Physica may refer to: * Physics (Aristotle) * ''Physica'', a twelfth-century medical text by Hildegard of Bingen * ''Physica'' (journal), a Dutch scientific journal :* ''Physica A'' :* ''Physica B'' ;* ''Physica C'' :* ''Physica D'' :* ''Physica E'' * ''Physica Scripta ''Physica Scripta'' is an international scientific journal for experimental and theoretical physics. It was established in 1970 as the successor of ''Arkiv för Fysik'' and published by the Royal Swedish Academy of Sciences (KVA). Since 2006, it ha ...

Statistical Model
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of Sample (statistics), sample data (and similar data from a larger Statistical population, population). A statistical model represents, often in considerably idealized form, the Data generating process, data-generating process. When referring specifically to probability, probabilities, the corresponding term is probabilistic model. All Statistical hypothesis testing, statistical hypothesis tests and all Estimator, statistical estimators are derived via statistical models. More generally, statistical models are part of the foundation of statistical inference. A statistical model is usually specified as a mathematical relationship between one or more random variables and other non-random variables. As such, a statistical model is "a formal representation of a theory" (Herman J. Adèr, Herman Adèr quoting Kenneth A. Bollen, Kenneth Bollen). Introduction Informally, a ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Superposition Principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input ''A'' produces response ''X'', and input ''B'' produces response ''Y'', then input (''A'' + ''B'') produces response (''X'' + ''Y''). A function F(x) that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity F(x_1 + x_2) = F(x_1) + F(x_2) and homogeneity F(ax) = a F(x) for scalar . This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathemat ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]