|
Sublime Number
In number theory, a sublime number is a positive integer which has a perfect number In number theory, a perfect number is a positive integer that is equal to the sum of its positive proper divisors, that is, divisors excluding the number itself. For instance, 6 has proper divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfec ... of positive factors (including itself), and whose positive factors add up to another perfect number. The number 12, for example, is a sublime number. It has a perfect number of positive factors ( 6): 1, 2, 3, 4, 6, and 12, and the sum of these is again a perfect number: 1 + 2 + 3 + 4 + 6 + 12 = 28. , there are only two known sublime numbers: 12 and (2126)(261 − 1)(231 − 1)(219 − 1)(27 − 1)(25 − 1)(23 − 1) . Clifford A. Pickover, ''Wonders of Numbers, Adventures in Mathematics, Mind and Meaning'' New York: Oxford University Press (2003): 215 The second of these has 76 decimal digits: :6,086,555,670,238,378,989,670,371,734,243,169,622 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Number Theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example, rational numbers), or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory can often be understood through the study of Complex analysis, analytical objects, such as the Riemann zeta function, that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, as for instance how irrational numbers can be approximated by fractions (Diophantine approximation). Number theory is one of the oldest branches of mathematics alongside geometry. One quirk of number theory is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set (mathematics), set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and Square root of 2, are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Perfect Number
In number theory, a perfect number is a positive integer that is equal to the sum of its positive proper divisors, that is, divisors excluding the number itself. For instance, 6 has proper divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfect number. The next perfect number is 28, since 1 + 2 + 4 + 7 + 14 = 28. The first four perfect numbers are 6 (number), 6, 28 (number), 28, 496 (number), 496 and 8128 (number), 8128. The sum of proper divisors of a number is called its aliquot sum, so a perfect number is one that is equal to its aliquot sum. Equivalently, a perfect number is a number that is half the sum of all of its positive divisors; in symbols, \sigma_1(n)=2n where \sigma_1 is the sum-of-divisors function. This definition is ancient, appearing as early as Euclid's Elements, Euclid's ''Elements'' (VII.22) where it is called (''perfect'', ''ideal'', or ''complete number''). Euclid also proved a formation rule (IX.36) whereby \frac is an even perfect number whenever q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Factorization
In mathematics, factorization (or factorisation, see American and British English spelling differences#-ise, -ize (-isation, -ization), English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several ''Factor (arithmetic), factors'', usually smaller or simpler objects of the same kind. For example, is an ''integer factorization'' of , and is a ''polynomial factorization'' of . Factorization is not usually considered meaningful within number systems possessing division ring, division, such as the real number, real or complex numbers, since any x can be trivially written as (xy)\times(1/y) whenever y is not zero. However, a meaningful factorization for a rational number or a rational function can be obtained by writing it in lowest terms and separately factoring its numerator and denominator. Factorization was first considered by Greek mathematics, ancient Greek mathematicians in the case of integers. They proved the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
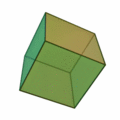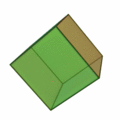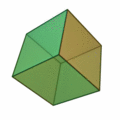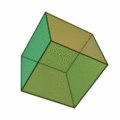
12 (number)
12 (twelve) is the natural number following 11 (number), 11 and preceding 13 (number), 13. Twelve is the 3rd superior highly composite number, the 3rd colossally abundant number, the 5th highly composite number, and is divisible by the numbers from 1 (number), 1 to 4 (number), 4, and 6 (number), 6, a large number of divisors comparatively. It is central to many systems of timekeeping, including the Gregorian calendar, Western calendar and time, units of time of day, and frequently appears in the world's major religions. Name Twelve is the largest number with a monosyllable, single-syllable name in English language, English. Early Germanic languages, Germanic numbers have been theorized to have been non-decimal: evidence includes the unusual phrasing of 11 (number), eleven and twelve, the long hundred, former use of "hundred" to refer to groups of 120 (number), 120, and the presence of glosses such as "tentywise" or "ten-count" in medieval texts showing that writers could not pres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
6 (number)
6 (six) is the natural number following 5 and preceding 7. It is a composite number and the smallest perfect number. In mathematics A six-sided polygon is a hexagon, one of the three regular polygons capable of tiling the plane. A hexagon also has 6 edges as well as 6 internal and external angles. 6 is the second smallest composite number. It is also the first number that is the sum of its proper divisors, making it the smallest perfect number. It is also the only perfect number that doesn't have a digital root of 1. 6 is the first unitary perfect number, since it is the sum of its positive proper unitary divisors, without including itself. Only five such numbers are known to exist. 6 is the largest of the four all-Harshad numbers. 6 is the 2nd superior highly composite number, the 2nd colossally abundant number, the 3rd triangular number, the 4th highly composite number, a pronic number, a congruent number, a harmonic divisor number, and a semiprime. 6 is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
28 (number)
28 (twenty-eight) is the natural number following 27 (number), 27 and preceding 29 (number), 29. In mathematics Twenty-eight is a composite number and the second perfect number as it is the sum of its proper divisors: 1+2+4+7+14=28. As a perfect number, it is related to the Mersenne prime 7, since 2^\times (2^-1)=28. The next perfect number is 496 (number), 496, the previous being 6 (number), 6. Though perfect, 28 is not the aliquot sum of any other number other than itself; thus, it is not part of a multi-number aliquot sequence. Twenty-eight is the sum of the totient function for the first nine integers. Since the greatest prime factor of 28^+1=785 is 157, which is more than 28 twice, 28 is a Størmer number. Twenty-eight is a harmonic divisor number, a happy number, the 7th triangular number, a hexagonal number, a Leyland number#Leyland number of the second kind, Leyland number of the second kind (2^6-6^2), and a centered nonagonal number. It appears in the Padovan sequ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Clifford A
Clifford may refer to: People * Clifford (name), an English given name and surname, includes a list of people with that name *William Kingdon Clifford * Baron Clifford *Baron Clifford of Chudleigh *Baron de Clifford * Clifford baronets * Clifford family (bankers) * Jaryd Clifford * Justice Clifford (other) * Lord Clifford (other) Arts, entertainment, and media *''Clifford the Big Red Dog'', a series of children's books ** Clifford (character), the central character of ''Clifford the Big Red Dog'' ** ''Clifford the Big Red Dog'' (2000 TV series), 2000 animated TV series **'' Clifford's Puppy Days'', 2003 animated TV series **'' Clifford's Really Big Movie'', 2004 animated movie ** ''Clifford the Big Red Dog'' (2019 TV series), 2019 animated TV series ** ''Clifford the Big Red Dog'' (film), 2021 live-action movie * ''Clifford'' (film), a 1994 film directed by Paul Flaherty * Clifford (Muppet) Mathematics *Clifford algebra, a type of associative algebra, named after ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Divisor Function
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (including 1 and the number itself). It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum. A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function. Definition The sum of positive divisors function ''σ''''z''(''n''), for a real or complex number ''z'', is defined as the sum of the ''z''th powers of the positive divisors of ''n''. It can be expressed in sigma notation as :\sigma_z(n)=\sum_ d^z\,\! , where is shorthand fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |