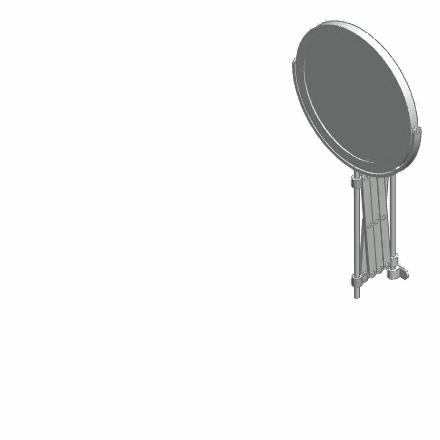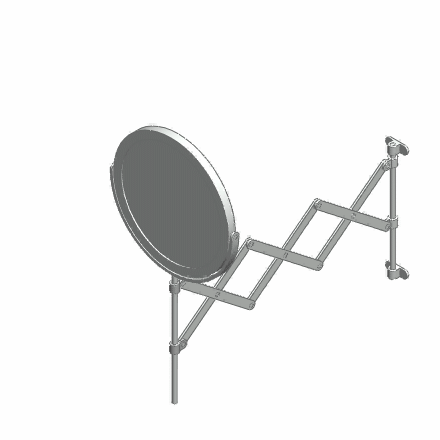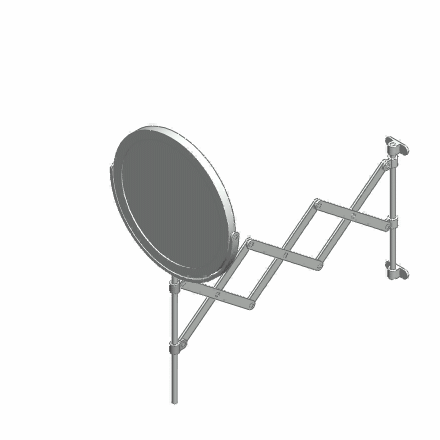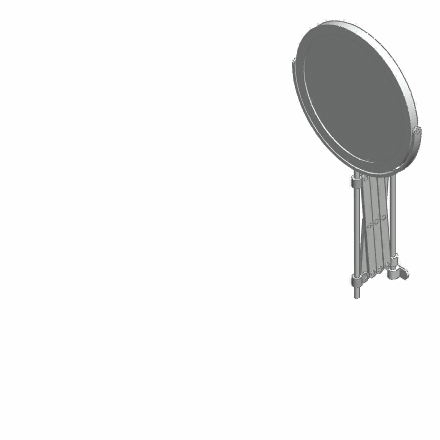|
Stuck Unknot
In mathematics, a stuck unknot is a closed polygonal chain in three-dimensional space (a skew polygon) that is topologically equal to the unknot but cannot be deformed to a simple polygon when interpreted as a mechanical linkage, by rigid length-preserving and non-self-intersecting motions of its segments.G. T. Toussaint, "A new class of stuck unknots in Pol-6," ''Contributions to Algebra and Geometry'', Vol. 42, No. 2, 2001, pp. 301–306. Similarly a stuck open chain is an open polygonal chain such that the segments may not be aligned by moving rigidly its segments. Topologically such a chain can be unknotted, but the limitation of using only rigid motions of the segments can create nontrivial knots in such a chain. Consideration of such "stuck" configurations arises in the study of molecular chains in biochemistry Biochemistry, or biological chemistry, is the study of chemical processes within and relating to living organisms. A sub-discipline of both chemistry and biology ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
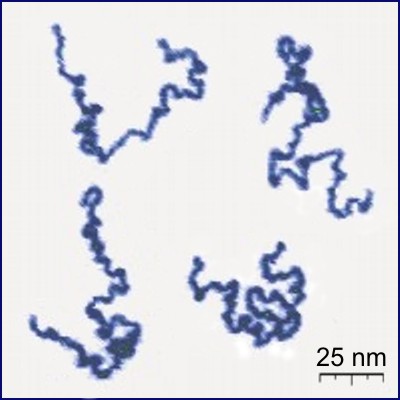
Polygonal Chain
In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points (A_1, A_2, \dots, A_n) called its vertices. The curve itself consists of the line segments connecting the consecutive vertices. Variations Simple A simple polygonal chain is one in which only consecutive segments intersect and only at their endpoints. Closed A closed polygonal chain is one in which the first vertex coincides with the last one, or, alternatively, the first and the last vertices are also connected by a line segment. A simple closed polygonal chain in the plane is the boundary of a simple polygon. Often the term "polygon" is used in the meaning of "closed polygonal chain", but in some cases it is important to draw a distinction between a polygonal area and a polygonal chain. A space closed polygonal chain is also known as a skew "polygon". Monotone A polygonal chain is called ''monotone'' if there is a strai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Polygon
In geometry, a skew polygon is a closed polygonal chain in Euclidean space. It is a figure (geometry), figure similar to a polygon except its Vertex (geometry), vertices are not all coplanarity, coplanar. While a polygon is ordinarily defined as a plane figure, the edge (geometry), edges and vertices of a skew polygon form a space curve. Skew polygons must have at least four vertices. The ''interior'' surface (geometry), surface and corresponding area measure of such a polygon is not uniquely defined. Skew infinite polygons (apeirogons) have vertices which are not all colinear. A zig-zag skew polygon or antiprismatic polygonRegular complex polytopes, p. 6 has vertices which alternate on two parallel planes, and thus must be even-sided. Regular skew polygons in 3 dimensions (and regular skew apeirogons in two dimensions) are always zig-zag. Skew polygons in three dimensions A regular skew polygon is a faithful symmetric realization of a polygon in dimension greater than 2. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unknot
In the knot theory, mathematical theory of knots, the unknot, not knot, or trivial knot, is the least knotted of all knots. Intuitively, the unknot is a closed loop of rope without a Knot (mathematics), knot tied into it, unknotted. To a knot theorist, an unknot is any embedding, embedded Topological sphere, topological circle in the 3-sphere that is ambient isotopy, ambient isotopic (that is, deformable) to a geometrically round circle, the standard unknot. The unknot is the only knot that is the boundary of an embedded disk (mathematics), disk, which gives the characterization that only unknots have Seifert surface, Seifert genus 0. Similarly, the unknot is the identity element with respect to the knot sum operation. Unknotting problem Deciding if a particular knot is the unknot was a major driving force behind knot invariants, since it was thought this approach would possibly give an efficient algorithm to unknotting problem, recognize the unknot from some presentation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Polygon
In geometry, a simple polygon is a polygon that does not Intersection (Euclidean geometry), intersect itself and has no holes. That is, it is a Piecewise linear curve, piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons. The sum of external angles of a simple polygon is 2\pi. Every simple polygon with n sides can be polygon triangulation, triangulated by n-3 of its diagonals, and by the art gallery theorem its interior is visible from some \lfloor n/3\rfloor of its vertices. Simple polygons are commonly seen as the input to computational geometry problems, including point in polygon testing, area computation, the convex hull of a simple polygon, triangulation, and Euclidean shortest paths. Other constructions in geometry related to simple polygons include Schwarz–Christoffel mapping, used to find conformal maps involving simple polygons, polygonalizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linkage (mechanical)
A mechanical linkage is an assembly of systems connected so as to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for example, and are called joints. A linkage modeled as a network of rigid links and ideal joints is called a kinematic chain. Linkages may be constructed from open chains, closed chains, or a combination of open and closed chains. Each link in a chain is connected by a joint to one or more other links. Thus, a kinematic chain can be modeled as a graph in which the links are paths and the joints are vertices, which is called a linkage graph. The movement of an ideal joint is generally associated with a subgroup of the group of Euclidean displacements. The number of parameters in the subgroup is called the degrees of freedom (DOF) of the joint. Mechanical linkages are usually designe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nontrivial
In mathematics, the adjective trivial is often used to refer to a claim or a case which can be readily obtained from context, or a particularly simple object possessing a given structure (e.g., group (mathematics), group, topological space). The noun triviality usually refers to a simple technical aspect of some proof or definition. The origin of the term in mathematical language comes from the medieval Trivium (education), trivium curriculum, which distinguishes from the more difficult quadrivium curriculum. The opposite of trivial is nontrivial, which is commonly used to indicate that an example or a solution is not simple, or that a statement or a theorem is not easy to prove. Triviality does not have a rigorous definition in mathematics. It is Subjectivity and objectivity (philosophy), subjective, and often determined in a given situation by the knowledge and experience of those considering the case. Trivial and nontrivial solutions In mathematics, the term "trivial" is ofte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polymer
A polymer () is a chemical substance, substance or material that consists of very large molecules, or macromolecules, that are constituted by many repeat unit, repeating subunits derived from one or more species of monomers. Due to their broad spectrum of properties, both synthetic and natural polymers play essential and ubiquitous roles in everyday life. Polymers range from familiar synthetic plastics such as polystyrene to natural biopolymers such as DNA and proteins that are fundamental to biological structure and function. Polymers, both natural and synthetic, are created via polymerization of many small molecules, known as monomers. Their consequently large molecular mass, relative to small molecule compound (chemistry), compounds, produces unique physical property, physical properties including toughness, high rubber elasticity, elasticity, viscoelasticity, and a tendency to form Amorphous solid, amorphous and crystallization of polymers, semicrystalline structures rath ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biochemistry
Biochemistry, or biological chemistry, is the study of chemical processes within and relating to living organisms. A sub-discipline of both chemistry and biology, biochemistry may be divided into three fields: structural biology, enzymology, and metabolism. Over the last decades of the 20th century, biochemistry has become successful at explaining living processes through these three disciplines. Almost all List of life sciences, areas of the life sciences are being uncovered and developed through biochemical methodology and research.#Voet, Voet (2005), p. 3. Biochemistry focuses on understanding the chemical basis that allows biomolecule, biological molecules to give rise to the processes that occur within living Cell (biology), cells and between cells,#Karp, Karp (2009), p. 2. in turn relating greatly to the understanding of tissue (biology), tissues and organ (anatomy), organs as well as organism structure and function.#Miller, Miller (2012). p. 62. Biochemistry is closely ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |