|
Strongly Measurable
Strong measurability has a number of different meanings, some of which are explained below. Values in Banach spaces For a function ''f'' with values in a Banach space (or Fréchet space), ''strong measurability'' usually means Bochner measurability. However, if the values of ''f'' lie in the space \mathcal(X,Y) of continuous linear operators from ''X'' to ''Y'', then often ''strong measurability'' means that the operator ''f(x)'' is Bochner measurable for each fixed ''x'' in the domain of ''f'', whereas the Bochner measurability of ''f'' is called ''uniform measurability'' (cf. " uniformly continuous" vs. "strongly continuous In mathematics, a strong topology is a topology which is stronger than some other "default" topology. This term is used to describe different topologies depending on context, and it may refer to: * the final topology on the disjoint union * the top ..."). Bounded operators A family of bounded linear operators combined with the direct integral is strongly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach Space
In mathematics, more specifically in functional analysis, a Banach space (pronounced ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space. Banach spaces are named after the Polish mathematician Stefan Banach, who introduced this concept and studied it systematically in 1920–1922 along with Hans Hahn and Eduard Helly. Maurice René Fréchet was the first to use the term "Banach space" and Banach in turn then coined the term " Fréchet space." Banach spaces originally grew out of the study of function spaces by Hilbert, Fréchet, and Riesz earlier in the century. Banach spaces play a central role in functional analysis. In other areas of analysis, the spaces under study are often Banach spaces. Definition A Banach space is a com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fréchet Space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces ( normed vector spaces that are complete with respect to the metric induced by the norm). All Banach and Hilbert spaces are Fréchet spaces. Spaces of infinitely differentiable functions are typical examples of Fréchet spaces, many of which are typically Banach spaces. A Fréchet space X is defined to be a locally convex metrizable topological vector space (TVS) that is complete as a TVS, meaning that every Cauchy sequence in X converges to some point in X (see footnote for more details).Here "Cauchy" means Cauchy with respect to the canonical uniformity that every TVS possess. That is, a sequence x_ = \left(x_m\right)_^ in a TVS X is Cauchy if and only if for all neighborhoods U of the origin in X, x_m - x_n \in U whenever m and n are sufficiently large. Note that this definit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bochner Measurability
In mathematics – specifically, in functional analysis – a Bochner-measurable function taking values in a Banach space is a function that equals almost everywhere the limit of a sequence of measurable countably-valued functions, i.e., :f(t) = \lim_f_n(t)\textt, \, where the functions f_n each have a countable range and for which the pre-image f^\ is measurable for each ''x''. The concept is named after Salomon Bochner. Bochner-measurable functions are sometimes called strongly measurable, \mu-measurable or just measurable (or uniformly measurable in case that the Banach space is the space of continuous linear operators between Banach spaces). Properties The relationship between measurability and weak measurability is given by the following result, known as Pettis' theorem or Pettis measurability theorem. Function ''f'' is almost surely separably valued (or essentially separably valued) if there exists a subset ''N'' ⊆ ''X'' with ''μ''(''N' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Linear Operator
In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces. An operator between two normed spaces is a bounded linear operator if and only if it is a continuous linear operator. Continuous linear operators Characterizations of continuity Suppose that F : X \to Y is a linear operator between two topological vector spaces (TVSs). The following are equivalent: F is continuous. F is continuous at some point x \in X. F is continuous at the origin in X. if Y is locally convex then this list may be extended to include: for every continuous seminorm q on Y, there exists a continuous seminorm p on X such that q \circ F \leq p. if X and Y are both Hausdorff locally convex spaces then this list may be extended to include: F is weakly continuous and its transpose ^t F : Y^ \to X^ maps equicontinuous subsets of Y^ to equicontinuous subsets o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniformly Continuous
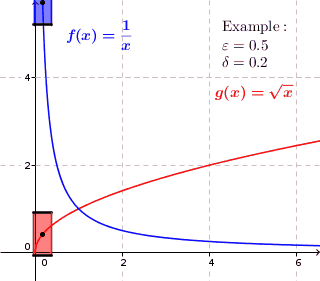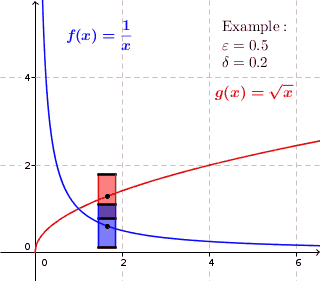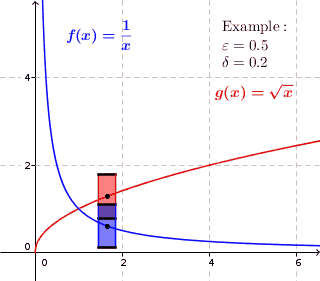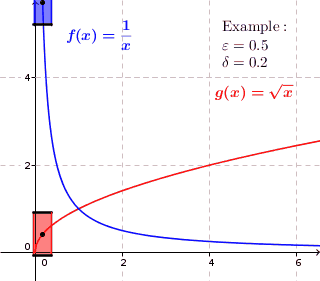
In mathematics, a real function f of real numbers is said to be uniformly continuous if there is a positive real number \delta such that function values over any function domain interval of the size \delta are as close to each other as we want. In other words, for a uniformly continuous real function of real numbers, if we want function value differences to be less than any positive real number \epsilon, then there is a positive real number \delta such that , f(x) - f(y), 0 there exists a real number \delta > 0 such that for every x,y \in X with d_1(x,y) 0 such that for every x,y \in X , , x - y, 0 \; \forall x \in X \; \forall y \in X : \, d_1(x,y) 0 , \forall x \in X , and \forall y \in X ) are used. * Alternatively, f is said to be uniformly continuous if there is a function of all positive real numbers \varepsilon, \delta(\varepsilon) representing the maximum positive real number, such that for every x,y \in X if d_1(x,y) 0 such that for every y \in X w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strongly Continuous
In mathematics, a strong topology is a topology which is stronger than some other "default" topology. This term is used to describe different topologies depending on context, and it may refer to: * the final topology on the disjoint union * the topology arising from a norm * the strong operator topology * the strong topology (polar topology), which subsumes all topologies above. A topology τ is stronger than a topology σ (is a finer topology) if τ contains all the open sets of σ. In algebraic geometry, it usually means the topology of an algebraic variety as complex manifold or subspace of complex projective space, as opposed to the Zariski topology (which is rarely even a Hausdorff space). See also * Weak topology In mathematics, weak topology is an alternative term for certain initial topologies, often on topological vector spaces or spaces of linear operators, for instance on a Hilbert space. The term is most commonly used for the initial topology of a ... {{sia, ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Integral
In mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers in the series ''On Rings of Operators''. One of von Neumann's goals in this paper was to reduce the classification of (what are now called) von Neumann algebras on separable Hilbert spaces to the classification of so-called factors. Factors are analogous to full matrix algebras over a field, and von Neumann wanted to prove a continuous analogue of the Artin–Wedderburn theorem classifying semi-simple rings. Results on direct integrals can be viewed as generalizations of results about finite-dimensional C*-algebras of matrices; in this case the results are easy to prove directly. The infinite-dimensional case is complicated by measure-theoretic technicalities. Direct integral theory was al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a Set (mathematics), set together with an associative internal binary operation on it. The binary operation of a semigroup is most often denoted multiplication, multiplicatively: ''x''·''y'', or simply ''xy'', denotes the result of applying the semigroup operation to the ordered pair . Associativity is formally expressed as that for all ''x'', ''y'' and ''z'' in the semigroup. Semigroups may be considered a special case of magma (algebra), magmas, where the operation is associative, or as a generalization of group (mathematics), groups, without requiring the existence of an identity element or inverses. The closure axiom is implied by the definition of a binary operation on a set. Some authors thus omit it and specify three axioms for a group and only one axiom (associativity) for a semigroup. As in the case of groups or magmas, the semigroup operation need not be commutativity, commutative, so ''x''·''y'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach Spaces
In mathematics, more specifically in functional analysis, a Banach space (pronounced ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space. Banach spaces are named after the Polish mathematician Stefan Banach, who introduced this concept and studied it systematically in 1920–1922 along with Hans Hahn and Eduard Helly. Maurice René Fréchet was the first to use the term "Banach space" and Banach in turn then coined the term "Fréchet space." Banach spaces originally grew out of the study of function spaces by Hilbert, Fréchet, and Riesz earlier in the century. Banach spaces play a central role in functional analysis. In other areas of analysis, the spaces under study are often Banach spaces. Definition A Banach space is a complete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |