|
State-transition Matrix
In control theory, the state-transition matrix is a matrix whose product with the state vector x at an initial time t_0 gives x at a later time t. The state-transition matrix can be used to obtain the general solution of linear dynamical systems. Linear systems solutions The state-transition matrix is used to find the solution to a general state-space representation of a linear system in the following form : \dot(t) = \mathbf(t) \mathbf(t) + \mathbf(t) \mathbf(t) , \;\mathbf(t_0) = \mathbf_0 , where \mathbf(t) are the states of the system, \mathbf(t) is the input signal, \mathbf(t) and \mathbf(t) are matrix functions, and \mathbf_0 is the initial condition at t_0. Using the state-transition matrix \mathbf(t, \tau), the solution is given by: : \mathbf(t)= \mathbf (t, t_0)\mathbf(t_0)+\int_^t \mathbf(t, \tau)\mathbf(\tau)\mathbf(\tau)d\tau The first term is known as the zero-input response and represents how the system's state would evolve in the absence of any input. The se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control Stability theory, stability; often with the aim to achieve a degree of Optimal control, optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or Setpoint (control system), set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
State Space Representation
State most commonly refers to: * State (polity), a centralized political organization that regulates law and society within a territory **Sovereign state, a sovereign polity in international law, commonly referred to as a country **Nation state, a state where the majority identify with a single nation (with shared culture or ethnic group) ** Constituent state, a political subdivision of a state ** Federated state, constituent states part of a federation *** U.S. state * State of nature, a concept within philosophy that describes the way humans acted before forming societies or civilizations State may also refer to: Arts, entertainment, and media Literature * '' State Magazine'', a monthly magazine published by the U.S. Department of State * ''The State'' (newspaper), a daily newspaper in Columbia, South Carolina, United States * '' Our State'', a monthly magazine published in North Carolina and formerly called ''The State'' * The State (Larry Niven), a fictional future governm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
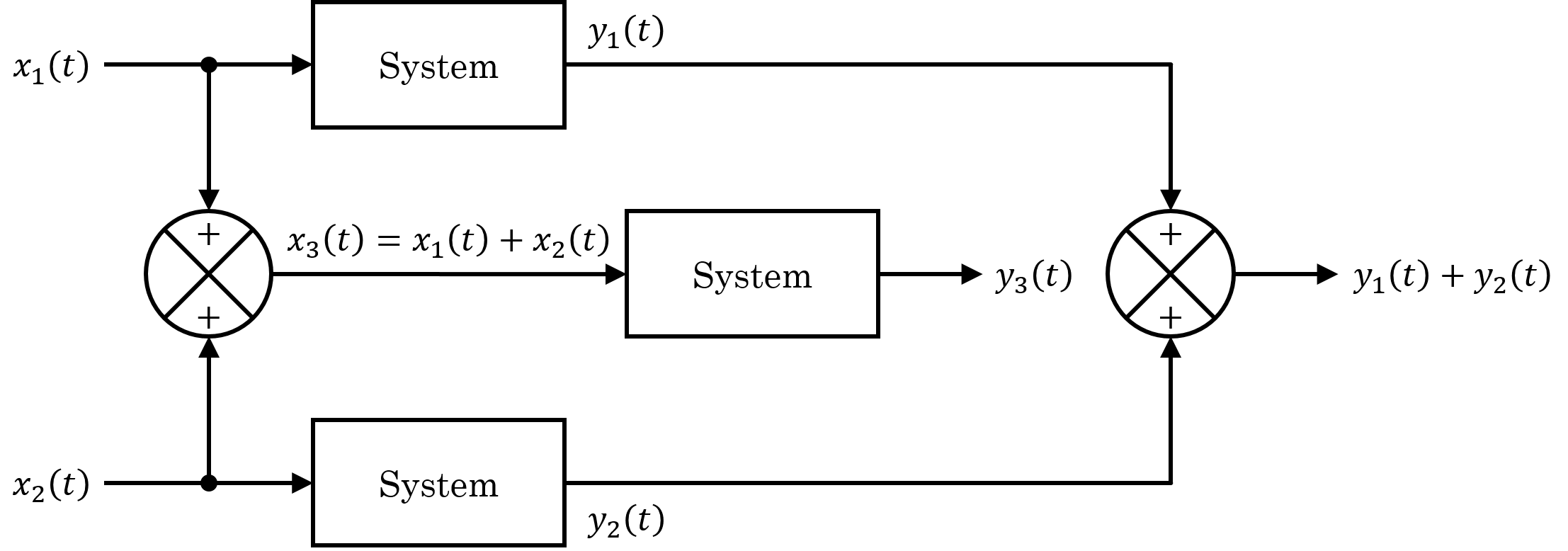
State-space Representation
In control engineering and system identification, a state-space representation is a mathematical model of a physical system that uses state variables to track how inputs shape system behavior over time through first-order differential equations or difference equations. These state variables change based on their current values and inputs, while outputs depend on the states and sometimes the inputs too. The state space (also called time-domain approach and equivalent to phase space in certain dynamical systems) is a geometric space where the axes are these state variables, and the system’s state is represented by a state vector. For linear, time-invariant, and finite-dimensional systems, the equations can be written in matrix form, offering a compact alternative to the frequency domain’s Laplace transforms for multiple-input and multiple-output (MIMO) systems. Unlike the frequency domain approach, it works for systems beyond just linear ones with zero initial conditions. Thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Function
In mathematics, every analytic function can be used for defining a matrix function that maps square matrices with complex entries to square matrices of the same size. This is used for defining the exponential of a matrix, which is involved in the closed-form solution of systems of linear differential equations. Extending scalar function to matrix functions There are several techniques for lifting a real function to a square matrix function such that interesting properties are maintained. All of the following techniques yield the same matrix function, but the domains on which the function is defined may differ. Power series If the analytic function has the Taylor expansion f(x) = c_0 + c_1 x + c_2 x^2 + \cdots then a matrix function A\mapsto f(A) can be defined by substituting by a square matrix: powers become matrix powers, additions become matrix sums and multiplications by coefficients become scalar multiplications. If the series converges for , x, < r, then t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Integral
A product integral is any product-based counterpart of the usual sum-based integral of calculus. The product integral was developed by the mathematician Vito Volterra in 1887 to solve systems of linear differential equations. A. Slavík''Product integration, its history and applications'' , Matfyzpress, Prague, 2007. Informal sketch The classical Riemann integral of a function f: ,bto\mathbb can be defined by the relation :\int_a^b f(x)\,dx = \lim_\sum f(x_i)\,\Delta x, where the limit is taken over all partitions of the interval ,b/math> whose norms approach zero. Product integrals are similar, but take the limit of a product instead of the limit of a sum. They can be thought of as "continuous" versions of "discrete" products. They are defined as :\prod_a^b \big(1 + f(x)\,dx\big) = \lim_ \prod \big(1 + f(x_i)\,\Delta x\big). For the case of f: ,bto\R, the product integral reduces exactly to the case of Lebesgue integration, that is, to classical calculus. Thus, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere. It has unique properties, for example when the identity matrix represents a geometric transformation, the object remains unchanged by the transformation. In other contexts, it is analogous to multiplying by the number 1. Terminology and notation The identity matrix is often denoted by I_n, or simply by I if the size is immaterial or can be trivially determined by the context. I_1 = \begin 1 \end ,\ I_2 = \begin 1 & 0 \\ 0 & 1 \end ,\ I_3 = \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end ,\ \dots ,\ I_n = \begin 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end. The term unit matrix has also been widely used, but the term ''identity matrix'' is now standard. The term ''unit matrix'' is ambiguous, because it is also used for a matrix of on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-ordering
In theoretical physics, path-ordering is the procedure (or a meta-operator \mathcal P) that orders a product of operators according to the value of a chosen parameter: :\mathcal P \left\ \equiv O_(\sigma_) O_(\sigma_) \cdots O_(\sigma_). Here ''p'' is a permutation that orders the parameters by value: :p : \ \to \ :\sigma_ \leq \sigma_ \leq \cdots \leq \sigma_. For example: :\mathcal P \left\ = O_4(1) O_2(2) O_3(3) O_1(4) . In many fields of physics, the most common type of path-ordering is time-ordering, which is discussed in detail below. Examples If an operator is not simply expressed as a product, but as a function of another operator, we must first perform a Taylor expansion of this function. This is the case of the Wilson loop, which is defined as a path-ordered exponential to guarantee that the Wilson loop encodes the holonomy of the gauge connection. The parameter ''σ'' that determines the ordering is a parameter describing the contour, and because the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnus Expansion
In mathematics and physics, the Magnus expansion, named after Wilhelm Magnus (1907–1990), provides an exponential representation of the product integral solution of a first-order homogeneous linear differential equation for a linear operator. In particular, it furnishes the fundamental matrix of a system of linear ordinary differential equations of order with varying coefficients. The exponent is aggregated as an infinite series, whose terms involve multiple integrals and nested commutators. The deterministic case Magnus approach and its interpretation Given the coefficient matrix , one wishes to solve the initial-value problem associated with the linear ordinary differential equation : Y'(t) = A(t) Y(t), \quad Y(t_0) = Y_0 for the unknown -dimensional vector function . When ''n'' = 1, the solution is given as a product integral : Y(t) = \exp \left( \int_^t A(s)\,ds \right) Y_0. This is still valid for ''n'' > 1 if the matrix satisfies for any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Matrix (linear Differential Equation)
In mathematics, a fundamental matrix of a system of ''n'' homogeneous linear ordinary differential equations \dot(t) = A(t) \mathbf(t) is a matrix-valued function \Psi(t) whose columns are linearly independent solutions of the system. Then every solution to the system can be written as \mathbf(t) = \Psi(t) \mathbf, for some constant vector \mathbf (written as a column vector of height ). A matrix-valued function \Psi is a fundamental matrix of \dot(t) = A(t) \mathbf(t) if and only if \dot(t) = A(t) \Psi(t) and \Psi is a non-singular matrix for all Control theory The fundamental matrix is used to express the state-transition matrix, an essential component in the solution of a system of linear ordinary differential equations. See also * Flow *Linear differential equation *Liouville's formula In mathematics, Liouville's formula, also known as the Abel–Jacobi–Liouville identity, is an equation that expresses the determinant of a square-matrix solution of a first-o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-invariant
In control theory, a time-invariant (TI) system has a time-dependent system function that is not a direct function of time. Such systems are regarded as a class of systems in the field of system analysis. The time-dependent system function is a function of the time-dependent input function. If this function depends ''only'' indirectly on the time-domain (via the input function, for example), then that is a system that would be considered time-invariant. Conversely, any direct dependence on the time-domain of the system function could be considered as a "time-varying system". Mathematically speaking, "time-invariance" of a system is the following property: :''Given a system with a time-dependent output function , and a time-dependent input function , the system will be considered time-invariant if a time-delay on the input directly equates to a time-delay of the output function. For example, if time is "elapsed time", then "time-invariance" implies that the relationship betw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Exponential
In mathematics, the matrix exponential is a matrix function on square matrix, square matrices analogous to the ordinary exponential function. It is used to solve systems of linear differential equations. In the theory of Lie groups, the matrix exponential gives the exponential map (Lie theory), exponential map between a matrix Lie algebra and the corresponding Lie group. Let be an real number, real or complex number, complex matrix (mathematics), matrix. The exponential of , denoted by or , is the matrix given by the power series e^X = \sum_^\infty \frac X^k where X^0 is defined to be the identity matrix I with the same dimensions as X, and . The series always converges, so the exponential of is well-defined. Equivalently, e^X = \lim_ \left(I + \frac \right)^k for integer-valued , where is the identity matrix. Equivalently, given by the solution to the differential equation \frac d e^ = X e^, \quad e^ = I When is an diagonal matrix then will be an diagonal matr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |