|
Spherical Octant
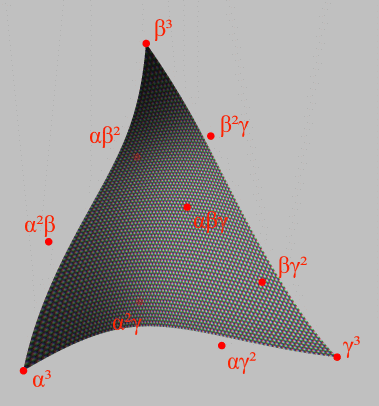
In geometry, an octant of a sphere is a spherical triangle with three right angles and three right sides. It is sometimes called a trirectangular (spherical) triangle. It is one face of a spherical octahedron. For a sphere embedded in three-dimensional Euclidean space, the vectors from the sphere's center to each vertex of an octant are the basis vectors of a Cartesian coordinate system relative to which the sphere is a unit sphere. The spherical octant itself is the intersection of the sphere with one octant of space. Uniquely among spherical triangles, the octant is its own polar triangle. The octant can be parametrized using a rational quartic Bézier triangle. The solid angle subtended by a spherical octant is /2 steradian or one-eight of a spat, the solid angle of a full sphere. See also * Trirectangular tetrahedron In geometry, a trirectangular tetrahedron is a tetrahedron where all three face angles at one vertex are right angles. That vertex is calle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octant Of A Sphere
In geometry, an octant of a sphere is a spherical triangle with three right angles and three right sides. It is sometimes called a trirectangular (spherical) triangle. It is one face of a spherical octahedron. For a sphere embedded in three-dimensional Euclidean space, the vectors from the sphere's center to each vertex of an octant are the basis vectors of a Cartesian coordinate system relative to which the sphere is a unit sphere. The spherical octant itself is the intersection of the sphere with one octant of space. Uniquely among spherical triangles, the octant is its own polar triangle. The octant can be parametrized using a rational quartic Bézier triangle. The solid angle subtended by a spherical octant is /2 steradian or one-eight of a spat, the solid angle of a full sphere. See also * Trirectangular tetrahedron In geometry, a trirectangular tetrahedron is a tetrahedron where all three face angles at one vertex are right angles. That vertex is called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative numbers, signed distances to the point from two fixed perpendicular oriented lines, called ''coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the ''Origin (mathematics), origin'' and has as coordinates. The axes direction (geometry), directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spat (angular Unit)
The spat (symbol sp), from the Latin ''spatium'' ("space"), is a unit of solid angle. 1 spat is equal to 4 steradians or approximately square degrees of solid angle . Thus it is the solid angle subtended by a complete sphere at its center. The whole sphere contains ~148.510 million square arcminutes and ~534.638 billion square arcseconds. See also * Turn (angle) — the plane angle counterpart of the spat, equivalent to 2 radian The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...s References Units of solid angle {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steradian
The steradian (symbol: sr) or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. A solid angle in the form of a circular cone can be projected onto a sphere from its centre, delineating a spherical cap where the cone intersects the sphere. The magnitude of the solid angle expressed in steradians is defined as the quotient of the surface area of the spherical cap and the square of the sphere's radius. This is analogous to the way a plane angle projected onto a circle delineates a circular arc on the circumference, whose length is proportional to the angle. Steradians can be used to measure a solid angle of any projected shape. The solid angle subtended is the same as that of a cone with the same projected area. A solid angle of one steradian subtends a cone aperture of approximately 1.144 radians or 65.54 degrees. In the SI, solid angle i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the ''apex'' of the solid angle, and the object is said to '' subtend'' its solid angle at that point. In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a ''steradian'' (symbol: sr), which is equal to one square radian, sr = rad2. One steradian corresponds to one unit of area (of any shape) on the unit sphere surrounding the apex, so an object that blocks all rays from the apex would cover a number of steradians equal to the total surface area of the unit sphere, 4\pi. Solid angles can also be measured in squares of angular measures such as degrees, minutes, and seconds. A small object nearby may subtend the same solid angle as a larger object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bézier Triangle
A Bézier triangle is a special type of Bézier surface that is created by (Linearity, linear, Square (algebra), quadratic, Cube (algebra), cubic or higher degree) interpolation of control points. ''n''th-order Bézier triangle A general ''n''th-order Bézier triangle has (''n'' +1)(''n'' + 2)/2 Control point (mathematics), control points ''α''''i''''β''''j''''γ''''k'' where ''i'', ''j'', ''k'' are non-negative integers such that ''i'' + ''j'' + ''k'' = ''n''. The surface is then defined as : (\alpha s + \beta t + \gamma u)^n = \sum_ s^i t^j u^k \alpha^i \beta^j \gamma^k = \sum_ \frac s^i t^j u^k \alpha^i \beta^j \gamma^k for all non-negative real numbers ''s'' + ''t'' + ''u'' = 1. With Linearity, linear order (n=1), the resulting Bézier triangle is actually a regular flat triangle, with the triangle vertices equaling the three control points. A Square (algebra), quadratic (n=2) Bézier tri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Triangle
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook ''Spherical trigonometry for the use of colleges and Schools''. Since then, significant developments have been the application of vector methods, quaternion methods, and the use of numerical methods. P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octant (solid Geometry)
An octant in solid geometry is one of the eight divisions of a Euclidean three-dimensional coordinate system defined by the signs of the coordinates. It is analogous to the two-dimensional ''quadrant'' and the one-dimensional ''ray''. The generalization of an octant is called ''orthant'' or ''hyperoctant''. Naming and numbering A convention for naming an octant is to give its list of signs, e.g. (+,−,−) or (−,+,−). Octant (+,+,+) is sometimes referred to as the ''first octant'', although similar ordinal name descriptors are not defined for the other seven octants. The advantages of using the (±,±,±) notation are its unambiguousness, and extensibility for higher dimensions. The following table shows the sign tuples together with likely ways to enumerate them. A binary enumeration with − as 1 can be easily generalized across dimensions. A binary enumeration with + as 1 defines the same order as balanced ternary. The Roman enumeration of the quadrants is in G ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Sphere
In mathematics, a unit sphere is a sphere of unit radius: the locus (mathematics), set of points at Euclidean distance 1 from some center (geometry), center point in three-dimensional space. More generally, the ''unit -sphere'' is an n-sphere, -sphere of unit radius in -dimensional Euclidean space; the unit circle is a special case, the unit -sphere in the Euclidean plane, plane. An (Open set, open) unit ball is the region inside of a unit sphere, the set of points of distance less than 1 from the center. A sphere or ball with unit radius and center at the origin (mathematics), origin of the space is called ''the'' unit sphere or ''the'' unit ball. Any arbitrary sphere can be transformed to the unit sphere by a combination of translation (geometry), translation and scaling (geometry), scaling, so the study of spheres in general can often be reduced to the study of the unit sphere. The unit sphere is often used as a model for spherical geometry because it has constant sectional cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis Vector
In mathematics, a set of elements of a vector space is called a basis (: bases) if every element of can be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to . The elements of a basis are called . Equivalently, a set is a basis if its elements are linearly independent and every element of is a linear combination of elements of . In other words, a basis is a linearly independent spanning set. A vector space can have several bases; however all the bases have the same number of elements, called the dimension of the vector space. This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. Basis vectors find applications in the study of crystal structures and frames of reference. Definition A basis of a vector space over a field (such as th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Euclidean vectors can be added and scaled to form a vector space. A '' vector quantity'' is a vector-valued physical quantity, including units of measurement and possibly a support, formulated as a '' directed line segment''. A vector is frequently depicted graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \stackrel \longrightarrow. A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word means 'carrier'. It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |