|
Sliced Inverse Regression
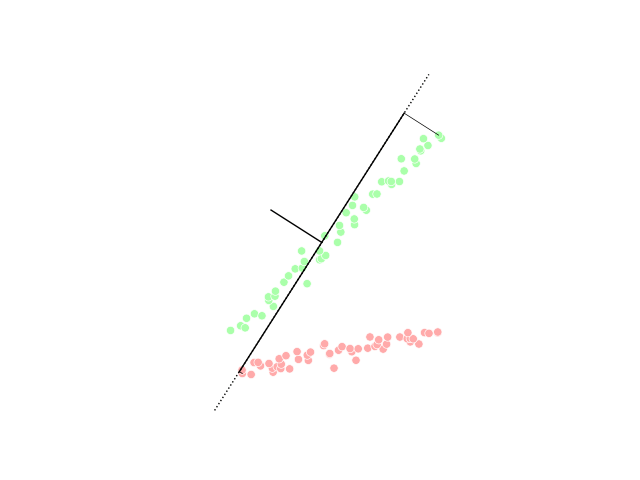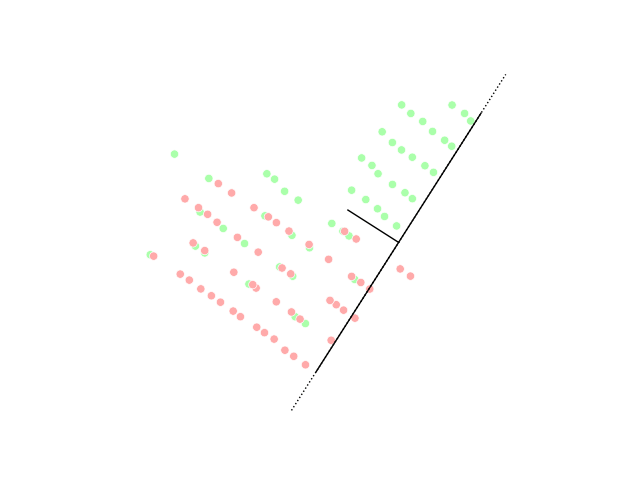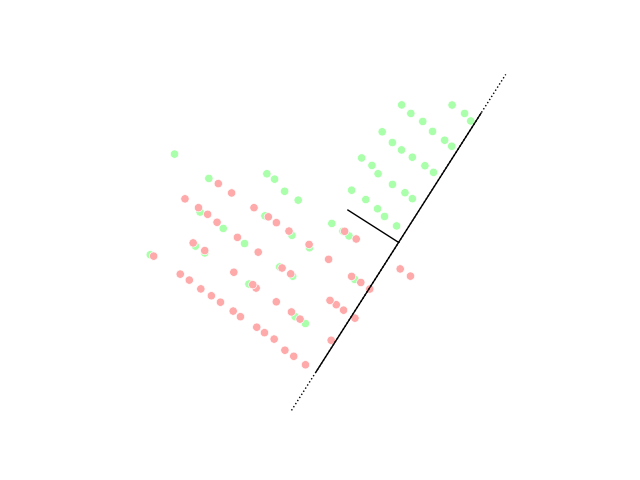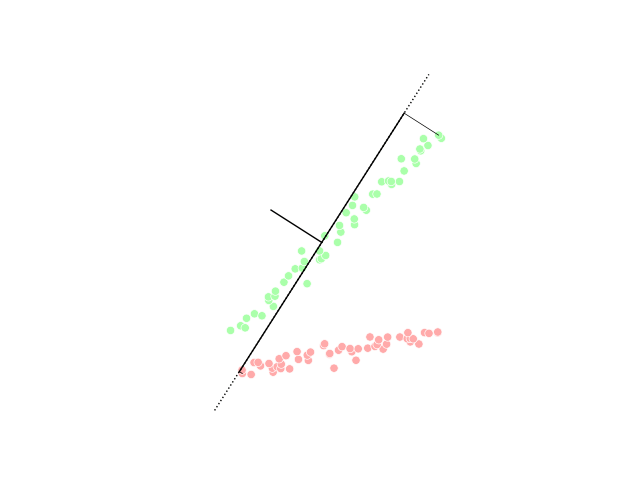
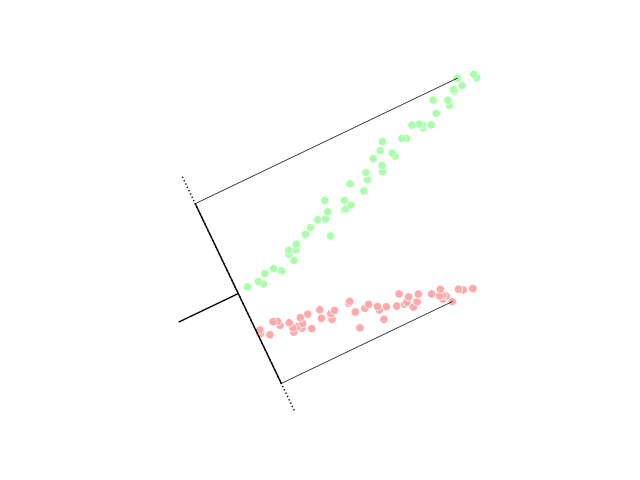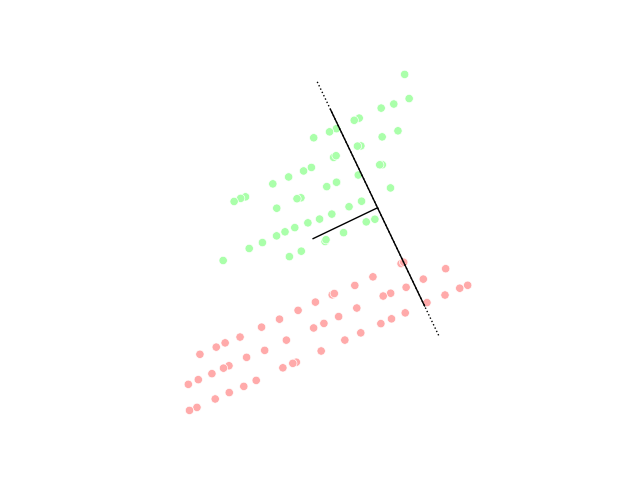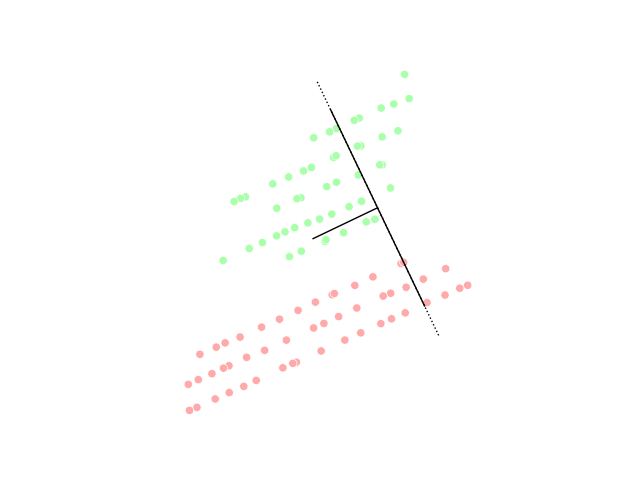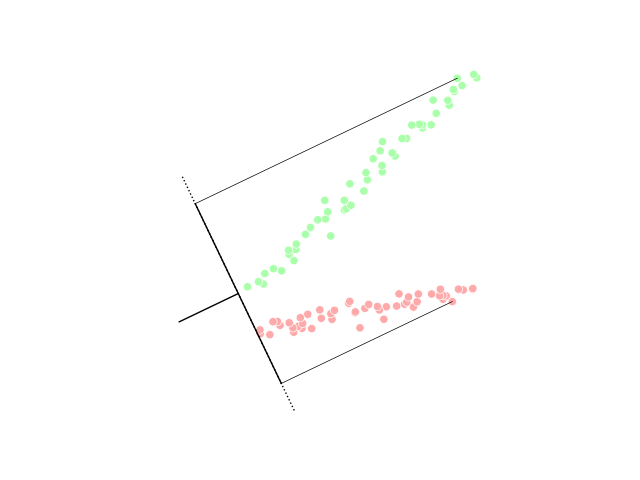
Sliced inverse regression (or SIR) is a tool for dimensionality reduction in the field of multivariate statistics. In statistics, regression analysis is a method of studying the relationship between a response variable ''y'' and its input variable \underline, which is a ''p''-dimensional vector. There are several approaches in the category of regression. For example, parametric methods include multiple linear regression, and non-parametric methods include local smoothing. As the number of observations needed to use local smoothing methods scales exponentially with high-dimensional data (as ''p'' grows), reducing the number of dimensions can make the operation computable. Dimensionality reduction aims to achieve this by showing only the most important dimension of the data. SIR uses the inverse regression curve, E(\underline\,, \,y), to perform a weighted principal component analysis. Model Given a response variable \,Y and a (random) vector X \in \R^p of explanatory variables, S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable (hard to control or deal with). Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Approaches can also be divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermedi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Statistics
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable. Multivariate statistics concerns understanding the different aims and background of each of the different forms of multivariate analysis, and how they relate to each other. The practical application of multivariate statistics to a particular problem may involve several types of univariate and multivariate analyses in order to understand the relationships between variables and their relevance to the problem being studied. In addition, multivariate statistics is concerned with multivariate probability distributions, in terms of both :*how these can be used to represent the distributions of observed data; :*how they can be used as part of statistical inference, particularly where several different quantities are of interest to the same analysis. Certain types of problems involving multivariate data, for example simple linear regression a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable (hard to control or deal with). Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Approaches can also be divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermedi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The American Statistical Association
The ''Journal of the American Statistical Association (JASA)'' is the primary journal published by the American Statistical Association, the main professional body for statisticians in the United States. It is published four times a year in March, June, September and December by Taylor & Francis, Ltd on behalf of the American Statistical Association. As a statistics journal it publishes articles primarily focused on the application of statistics, statistical theory and methods in economic, social, physical, engineering, and health sciences. The journal also includes reviews of academic books which are important to the advancement of the field. It had an impact factor of 2.063 in 2010, tenth highest in the "Statistics and Probability" category of '' Journal Citation Reports''. In a 2003 survey of statisticians, the ''Journal of the American Statistical Association'' was ranked first, among all journals, for "Applications of Statistics" and second (after ''Annals of Statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
