|
Simplification Of Disjunctive Antecedents
In formal semantics (natural language), formal semantics and philosophical logic, simplification of disjunctive antecedents (SDA) is the phenomenon whereby a disjunction in the antecedent of a conditional sentence, conditional appears to distributive property, distribute over the conditional as a whole. This inference is shown schematically below: # (A \lor B) \Rightarrow C \models (A \Rightarrow C) \land (B \Rightarrow C) This inference has been argued to be validity (logic), valid on the basis of sentence pairs such as that below, since Sentence 1 seems to imply Sentence 2. # If Yde or Dani had come to the party, it would have been fun. # If Yde had come to the party, it would be been fun and if Dani had come to the party, it would have been fun. The SDA inference was first discussed as a potential problem for the Counterfactual_conditional#Variably_strict_conditional, similarity analysis of counterfactuals. In these approaches, a counterfactual (A \lor B) > C is predicted to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Semantics (natural Language)
Formal semantics is the scientific study of linguistic meaning through formal tools from logic and mathematics. It is an interdisciplinary field, sometimes regarded as a subfield of both linguistics and philosophy of language. Formal semanticists rely on diverse methods to analyze natural language. Many examine the meaning of a sentence by studying the circumstances in which it would be true. They describe these circumstances using abstract mathematical models to represent entities and their features. The principle of compositionality helps them link the meaning of expressions to abstract objects in these models. This principle asserts that the meaning of a compound expression is determined by the meanings of its parts. Propositional and predicate logic are formal systems used to analyze the semantic structure of sentences. They introduce concepts like singular terms, predicates, quantifiers, and logical connectives to represent the logical form of natural language expres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strict Conditional
In logic, a strict conditional (symbol: \Box, or ⥽) is a conditional governed by a modal operator, that is, a logical connective of modal logic. It is logically equivalent to the material conditional of classical logic, combined with the necessity operator from modal logic. For any two propositions ''p'' and ''q'', the formula ''p'' → ''q'' says that ''p'' materially implies ''q'' while \Box (p \rightarrow q) says that ''p'' strictly implies ''q''. Strict conditionals are the result of Clarence Irving Lewis's attempt to find a conditional for logic that can adequately express indicative conditionals in natural language. They have also been used in studying Molinist theology. Avoiding paradoxes The strict conditionals may avoid paradoxes of material implication. The following statement, for example, is not correctly formalized by material implication: : If Bill Gates graduated in medicine, then Elvis never died. This condition should clearly be false: the degree of Bill ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philosophical Logic
Understood in a narrow sense, philosophical logic is the area of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. Some theorists conceive philosophical logic in a wider sense as the study of the scope and nature of logic in general. In this sense, philosophical logic can be seen as identical to the philosophy of logic, which includes additional topics like how to define logic or a discussion of the fundamental concepts of logic. The current article treats philosophical logic in the narrow sense, in which it forms one field of inquiry within the philosophy of logic. An important issue for philosophical logic is the question of how to classify the great variety of non-classical logical systems, many of which are of rather recent origin. One form of classification often found in the literature is to distinguish between extended logics and deviant logics. Logic itself can be defined as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to wor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semantics
Semantics is the study of linguistic Meaning (philosophy), meaning. It examines what meaning is, how words get their meaning, and how the meaning of a complex expression depends on its parts. Part of this process involves the distinction between sense and reference. Sense is given by the ideas and concepts associated with an expression while reference is the object to which an expression points. Semantics contrasts with syntax, which studies the rules that dictate how to create grammatically correct sentences, and pragmatics, which investigates how people use language in communication. Lexical semantics is the branch of semantics that studies word meaning. It examines whether words have one or several meanings and in what lexical relations they stand to one another. Phrasal semantics studies the meaning of sentences by exploring the phenomenon of compositionality or how new meanings can be created by arranging words. Formal semantics (natural language), Formal semantics relies o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Choice Inference
Free choice is a phenomenon in natural language where a linguistic disjunction appears to receive a logical conjunctive interpretation when it interacts with a modal operator. For example, the following English sentences can be interpreted to mean that the addressee can watch a movie ''and'' that they can also play video games, depending on their preference: # You can watch a movie or play video games. # You can watch a movie or you can play video games. Free choice inferences are a major topic of research in formal semantics and philosophical logic because they are not valid in classical systems of modal logic. If they were valid, then the semantics of natural language would validate the ''Free Choice Principle''. # ''Free Choice Principle'': \Diamond( P \lor Q) \rightarrow (\Diamond P \land \Diamond Q) This symbolic logic formula above is not valid in classical modal logic: Adding this principle as an axiom to standard modal logics would allow one to conclude \Diamond Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Logic
Modal logic is a kind of logic used to represent statements about Modality (natural language), necessity and possibility. In philosophy and related fields it is used as a tool for understanding concepts such as knowledge, obligation, and causality, causation. For instance, in epistemic modal logic, the well-formed_formula, formula \Box P can be used to represent the statement that P is known. In deontic modal logic, that same formula can represent that P is a moral obligation. Modal logic considers the inferences that modal statements give rise to. For instance, most epistemic modal logics treat the formula \Box P \rightarrow P as a Tautology_(logic), tautology, representing the principle that only true statements can count as knowledge. However, this formula is not a tautology in deontic modal logic, since what ought to be true can be false. Modal logics are formal systems that include unary operation, unary operators such as \Diamond and \Box, representing possibility and necessi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjunction
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is sunny or it is warm" can be represented in logic using the disjunctive formula S \lor W , assuming that S abbreviates "it is sunny" and W abbreviates "it is warm". In classical logic, disjunction is given a truth functional semantics according to which a formula \phi \lor \psi is true unless both \phi and \psi are false. Because this semantics allows a disjunctive formula to be true when both of its disjuncts are true, it is an ''inclusive'' interpretation of disjunction, in contrast with exclusive disjunction. Classical proof theoretical treatments are often given in terms of rules such as disjunction introduction and disjunction elimination. Disjunction has also been given numerous non-classical treatments, motivated by problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Choice Inference
Free choice is a phenomenon in natural language where a linguistic disjunction appears to receive a logical conjunctive interpretation when it interacts with a modal operator. For example, the following English sentences can be interpreted to mean that the addressee can watch a movie ''and'' that they can also play video games, depending on their preference: # You can watch a movie or play video games. # You can watch a movie or you can play video games. Free choice inferences are a major topic of research in formal semantics and philosophical logic because they are not valid in classical systems of modal logic. If they were valid, then the semantics of natural language would validate the ''Free Choice Principle''. # ''Free Choice Principle'': \Diamond( P \lor Q) \rightarrow (\Diamond P \land \Diamond Q) This symbolic logic formula above is not valid in classical modal logic: Adding this principle as an axiom to standard modal logics would allow one to conclude \Diamond Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
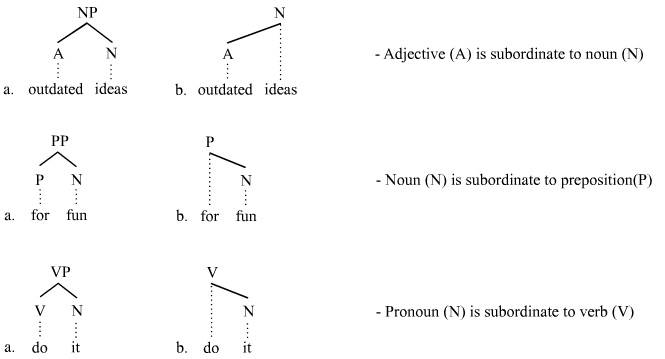
Subordination (linguistics)
In linguistics, subordination (abbreviated variously , , or ) is a principle of the hierarchical organization of linguistic units. While the principle is applicable in semantics, morphology, and phonology, most work in linguistics employs the term "subordination" in the context of syntax, and that is the context in which it is considered here. The syntactic units of sentences are often either subordinate or coordinate to each other. Hence an understanding of subordination is promoted by an understanding of coordination, and vice versa. Subordinate clauses Subordination as a concept of syntactic organization is associated closely with the distinction between ''coordinate'' and ''subordinate'' clauses. One clause is subordinate to another if it depends on it. The dependent clause is called a ''subordinate clause'' and the independent clause is called the ''main clause'' (= matrix clause). Subordinate clauses are usually introduced by subordinators (= subordinate conjunctions) such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicature
In pragmatics, a subdiscipline of linguistics, an implicature is something the speaker suggests or implies with an utterance, even though it is not literally expressed. Implicatures can aid in communicating more efficiently than by explicitly saying everything we want to communicate. The philosopher H. P. Grice coined the term in 1975. Grice distinguished ''conversational'' implicatures, which arise because speakers are expected to respect general rules of conversation, and ''conventional'' ones, which are tied to certain words such as "but" or "therefore". Take for example the following exchange: : A (to passerby): I am out of gas. : B: There is a gas station 'round the corner. Here, B does not say, but ''conversationally implicates'', that the gas station is open, because otherwise his utterance would not be relevant in the context. Conversational implicatures are classically seen as contrasting with entailments: they are not necessary or logical consequences of what is said, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Situation Semantics
In situation theory, situation semantics (pioneered by Jon Barwise and John Perry in the early 1980s) attempts to provide a solid theoretical foundation for reasoning about common-sense and real world situations, typically in the context of theoretical linguistics, theoretical philosophy, or applied natural language processing, Barwise and Perry Situations, unlike worlds, are not complete in the sense that every proposition or its negation holds in a world. According to ''Situations and Attitudes'', meaning is a relation between a discourse situation, a connective situation and a described situation. The original theory of ''Situations and Attitudes'' soon ran into foundational difficulties. A reformulation based on Peter Aczel's non-well-founded set theory was proposed by Barwise before this approach to the subject petered out in the early 1990s. HPSG Situation semantics is the first semantic theory that was used in head-driven phrase structure grammar (HPSG). Kratzer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |