|
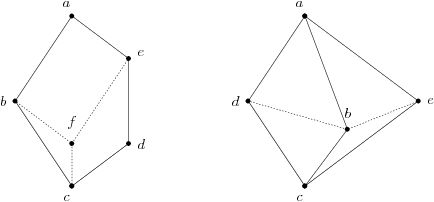
Simplex Graph
In graph theory, a branch of mathematics, the simplex graph of an undirected graph is itself a graph, with one node for each clique (a set of mutually adjacent vertices) in . Two nodes of are linked by an edge whenever the corresponding two cliques differ in the presence or absence of a single vertex. The empty set is included as one of the cliques of that are used to form the clique graph, as is every set of one vertex and every set of two adjacent vertices. Therefore, the simplex graph contains within it a subdivision of itself. The simplex graph of a complete graph is a hypercube graph, and the simplex graph of a cycle graph of length four or more is a gear graph. The simplex graph of the complement graph of a path graph is a Fibonacci cube. The complete subgraphs of can be given the structure of a median algebra: the median of three cliques , , and is formed by the vertices that belong to a majority of the three cliques. Any two vertices belonging to this median set mu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Majority Function
In Boolean logic, the majority function (also called the median operator) is the Boolean function that evaluates to false when half or more arguments are false and true otherwise, i.e. the value of the function equals the value of the majority of the inputs. Boolean circuits A ''majority gate'' is a logical gate used in circuit complexity and other applications of Boolean circuits. A majority gate returns true if and only if more than 50% of its inputs are true. For instance, in a full adder, the carry output is found by applying a majority function to the three inputs, although frequently this part of the adder is broken down into several simpler logical gates. Many systems have triple modular redundancy; they use the majority function for majority logic decoding to implement error correction. A major result in circuit complexity asserts that the majority function cannot be computed by AC0 circuits of subexponential size. Properties For any ''x'', ''y'', and ''z'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Operations
In the mathematical field of graph theory, graph operations are operations which produce new graphs from initial ones. They include both unary (one input) and binary (two input) operations. Unary operations Unary operations create a new graph from a single initial graph. Elementary operations Elementary operations or editing operations, which are also known as graph edit operations, create a new graph from one initial one by a simple local change, such as addition or deletion of a vertex or of an edge, merging and splitting of vertices, edge contraction, etc. The graph edit distance between a pair of graphs is the minimum number of elementary operations required to transform one graph into the other. Advanced operations Advanced operations create a new graph from an initial one by a complex change, such as: * transpose graph; * complement graph; * line graph; * graph minor; * graph rewriting; * power of graph; * dual graph; * medial graph; * quotient graph; * Y- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SIAM Journal On Discrete Mathematics
'' SIAM Journal on Discrete Mathematics'' is a peer-reviewed mathematics journal published quarterly by the Society for Industrial and Applied Mathematics (SIAM). The journal includes articles on pure and applied discrete mathematics. It was established in 1988, along with the ''SIAM Journal on Matrix Analysis and Applications'', to replace the '' SIAM Journal on Algebraic and Discrete Methods''. The journal is indexed by ''Mathematical Reviews'' and Zentralblatt MATH. Its 2009 MCQ was 0.57. According to the ''Journal Citation Reports'', the journal has a 2016 impact factor of 0.755. Although its official ISO abbreviation is ''SIAM J. Discrete Math.'', its publisher and contributors frequently use the shorter abbreviation ''SIDMA''. References External links * Discrete mathematics journals Academic journals established in 1988 English-language journals Discrete Mathematics Discrete mathematics is the study of mathematical structures that can be considered "discre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Tree
In mathematics, real trees (also called \mathbb R-trees) are a class of metric spaces generalising simplicial Tree (graph theory), trees. They arise naturally in many mathematical contexts, in particular geometric group theory and probability theory. They are also the simplest examples of Gromov hyperbolic spaces. Definition and examples Formal definition A metric space X is a real tree if it is a Geodesic metric space, geodesic space where every triangle is a tripod. That is, for every three points x, y, \rho \in X there exists a point c = x \wedge y such that the geodesic segments [\rho,x], [\rho,y] intersect in the segment [\rho,c] and also c \in [x,y]. This definition is equivalent to X being a "zero-hyperbolic space" in the sense of Gromov (all triangles are "zero-thin"). Real trees can also be characterised by a topology, topological property. A metric space X is a real tree if for any pair of points x, y \in X all topological embeddings \sigma of the segment [0,1] int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mycielskian
In the mathematical area of graph theory, the Mycielskian or Mycielski graph of an undirected graph is a larger graph formed from it by a construction of . The construction preserves the property of being triangle-free but increases the chromatic number; by applying the construction repeatedly to a triangle-free starting graph, Mycielski showed that there exist triangle-free graphs with arbitrarily large chromatic number. Construction Let the ''n'' vertices of the given graph ''G'' be ''v''1, ''v''2, . . . , ''v''n. The Mycielski graph μ(''G'') contains ''G'' itself as a subgraph, together with ''n''+1 additional vertices: a vertex ''u''''i'' corresponding to each vertex ''v''''i'' of ''G'', and an extra vertex ''w''. Each vertex ''u''''i'' is connected by an edge to ''w'', so that these vertices form a subgraph in the form of a star ''K''1,''n''. In addition, for each edge ''v''''i''''v''''j'' of ''G'', the Mycielski graph includes two edges, ''u''''i''''v''''j'' and ''v''''i' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Product Of Graphs
In graph theory, the Cartesian product of graphs and is a graph such that: * the vertex set of is the Cartesian product ; and * two vertices and are adjacent in if and only if either ** and is adjacent to in , or ** and is adjacent to in . The Cartesian product of graphs is sometimes called the box product of graphs arary 1969 The operation is associative, as the graphs and are naturally isomorphic. The operation is commutative as an operation on isomorphism classes of graphs, and more strongly the graphs and are naturally isomorphic, but it is not commutative as an operation on labeled graphs. The notation has often been used for Cartesian products of graphs, but is now more commonly used for another construction known as the tensor product of graphs. The square symbol is intended to be an intuitive and unambiguous notation for the Cartesian product, since it shows visually the four edges resulting from the Cartesian product of two edges. Examples * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatic Number
In graph theory, graph coloring is a methodic assignment of labels traditionally called "colors" to elements of a graph. The assignment is subject to certain constraints, such as that no two adjacent elements have the same color. Graph coloring is a special case of graph labeling. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an '' edge coloring'' assigns a color to each edges so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face (or region) so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle-free Graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs. By Turán's theorem, the ''n''-vertex triangle-free graph with the maximum number of edges is a complete bipartite graph in which the numbers of vertices on each side of the bipartition are as equal as possible. Triangle finding problem The triangle finding or triangle detection problem is the problem of determining whether a graph is triangle-free or not. When the graph does contain a triangle, algorithms are often required to output three vertices which form a triangle in the graph. It is possible to test whether a graph with m edges is triangle-free in time \tilde O\bigl(m^\bigr) where the \tilde O hides sub-polynomial factors. Here \omega is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clique Complex
Clique complexes, independence complexes, flag complexes, Whitney complexes and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques (complete subgraphs) of an undirected graph. Clique complex The clique complex of an undirected graph is an abstract simplicial complex (that is, a family of finite sets closed under the operation of taking subsets), formed by the sets of vertices in the cliques of . Any subset of a clique is itself a clique, so this family of sets meets the requirement of an abstract simplicial complex that every subset of a set in the family should also be in the family. The clique complex can also be viewed as a topological space in which each clique of vertices is represented by a simplex of dimension . The 1-skeleton of (also known as the ''underlying graph'' of the complex) is an undirected graph with a vertex for every 1-element set in the family and an edge for every 2- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributive Lattice
In mathematics, a distributive lattice is a lattice (order), lattice in which the operations of join and meet distributivity, distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union (set theory), union and intersection (set theory), intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to order isomorphism, isomorphism—given as such a lattice of sets. Definition As in the case of arbitrary lattices, one can choose to consider a distributive lattice ''L'' either as a structure of order theory or of universal algebra. Both views and their mutual correspondence are discussed in the article on lattice (order), lattices. In the present situation, the algebraic description appears to be more convenient. A lattice (''L'',∨,∧) is distributive if the following additional identity holds for all ''x'', ''y'', and ''z'' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipartite Graph
In the mathematics, mathematical field of graph theory, a bipartite graph (or bigraph) is a Graph (discrete mathematics), graph whose vertex (graph theory), vertices can be divided into two disjoint sets, disjoint and Independent set (graph theory), independent sets U and V, that is, every edge (graph theory), edge connects a Vertex (graph theory), vertex in U to one in V. Vertex sets U and V are usually called the ''parts'' of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycle (graph theory), cycles. The two sets U and V may be thought of as a graph coloring, coloring of the graph with two colors: if one colors all nodes in U blue, and all nodes in V red, each edge has endpoints of differing colors, as is required in the graph coloring problem.. In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a Gallery of named graphs, triangle: after one node is colored blue and another red, the third vertex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |