 |
Simple Harmonic Motion
In mechanics and physics, simple harmonic motion (sometimes abbreviated as ) is a special type of periodic motion an object experiences by means of a restoring force whose magnitude is directly proportional to the distance of the object from an equilibrium position and acts towards the equilibrium position. It results in an oscillation that is described by a sinusoid which continues indefinitely (if uninhibited by friction or any other dissipation of energy). Simple harmonic motion can serve as a mathematical model for a variety of motions, but is typified by the oscillation of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's law. The motion is sinusoidal in time and demonstrates a single resonant frequency. Other phenomena can be modeled by simple harmonic motion, including the motion of a simple pendulum, although for it to be an accurate model, the net force on the object at the end of the pendulum must be proportional to the dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Simple Harmonic Motion Orbit
Simple or SIMPLE may refer to: *Simplicity, the state or quality of being simple Arts and entertainment * Simple (album), ''Simple'' (album), by Andy Yorke, 2008, and its title track * Simple (Florida Georgia Line song), "Simple" (Florida Georgia Line song), 2018 * "Simple", a song by Johnny Mathis from the 1984 album ''A Special Part of Me'' * "Simple", a song by Collective Soul from the 1995 album ''Collective Soul (1995 album), Collective Soul'' * "Simple", a song by Katy Perry from the 2005 soundtrack to ''The Sisterhood of the Traveling Pants (film), The Sisterhood of the Traveling Pants'' * "Simple", a song by Khalil from the 2017 album ''Prove It All'' * "Simple", a song by Kreesha Turner from the 2008 album ''Passion (Kreesha Turner album), Passion'' * "Simple", a song by Ty Dolla Sign from the 2017 album ''Beach House 3'' deluxe version * Simple (video game series), ''Simple'' (video game series), budget-priced console games Businesses and organisations * Simple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Sinusoidal
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is '' simple harmonic motion''; as rotation, it corresponds to '' uniform circular motion''. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes. When any two sine waves of the same frequency (but arbitrary phase) are linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine waves with phases of zero and a quarter cycle, the ''sine'' and ''cosine'' co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Exertion
Exertion is the Action (physics), physical or perceived use of energy.Newton's Third Law, Elert, Glenn. “Forces.” ''Viscosity – The Physics Hypertextbook'', physics.info/newton-first/. Exertion traditionally connotes a strenuous or costly ''effort'', resulting in generation of force, initiation of motion, or in the performance of Mechanical work, work. It often relates to Exercise physiology, muscular activity and can be quantified, empirically and by measurable metabolic response. Physical In physics, ''exertion'' is the expenditure of energy against, or inductive of, inertia as described by Isaac Newton's Newton's laws of motion#Newton's third law, third law of motion. In physics, force exerted equivocates work done. The ability to do work can be either positive or negative depending on the direction of exertion relative to gravity. For example, a force exerted upwards, like lifting an object, creates positive work done on that object. Exertion often results in force genera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitude (mathematics), magnitude and Direction (geometry, geography), direction of a force are both important, force is a Euclidean vector, vector quantity. The SI unit of force is the newton (unit), newton (N), and force is often represented by the symbol . Force plays an important role in classical mechanics. The concept of force is central to all three of Newton's laws of motion. Types of forces often encountered in classical mechanics include Elasticity (physics), elastic, frictional, Normal force, contact or "normal" forces, and gravity, gravitational. The rotational version of force is torque, which produces angular acceleration, changes in the rotational speed of an object. In an extended body, each part applies forces on the adjacent pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Mechanical Equilibrium
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is zero. In addition to defining mechanical equilibrium in terms of force, there are many alternative definitions for mechanical equilibrium which are all mathematically equivalent. * In terms of momentum, a system is in equilibrium if the momentum of its parts is all constant. * In terms of velocity, the system is in equilibrium if velocity is constant. * In a rotational mechanical equilibrium the angular momentum of the object is conserved and the net torque is zero. More generally in conservative systems, equilibrium is established at a point in Configuration space (physics), configuration space where the gradient of the potential energy with respect to the generalized coordinates is zero. If a particle in equilibrium has zero velocity, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Harmonic Oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive constant. The harmonic oscillator model is important in physics, because any mass subject to a force in stable equilibrium acts as a harmonic oscillator for small vibrations. Harmonic oscillators occur widely in nature and are exploited in many manmade devices, such as clocks and radio circuits. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force ( damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Fixed Point (mathematics)
In mathematics, a fixed point (sometimes shortened to fixpoint), also known as an invariant point, is a value that does not change under a given transformation (mathematics), transformation. Specifically, for function (mathematics), functions, a fixed point is an element that is mapped to itself by the function. Any set of fixed points of a transformation is also an invariant set. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain of a function, domain and the codomain of , and . In particular, cannot have any fixed point if its domain is disjoint from its codomain. If is defined on the real numbers, it corresponds, in graphical terms, to a curve in the Euclidean plane, and each fixed-point corresponds to an intersection of the curve with the line , cf. picture. For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector quantities (in that they have Magnitude (mathematics), magnitude and Direction (geometry), direction). The orientation of an object's acceleration is given by the orientation of the ''net'' force acting on that object. The magnitude of an object's acceleration, as described by Newton's second law, is the combined effect of two causes: * the net balance of all external forces acting onto that object — magnitude is Direct proportionality, directly proportional to this net resulting force; * that object's mass, depending on the materials out of which it is made — magnitude is Inverse proportionality, inversely proportional to the object's mass. The International System of Units, SI unit for acceleration is metre per second squared (, \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Particle
In the physical sciences, a particle (or corpuscle in older texts) is a small localized object which can be described by several physical or chemical properties, such as volume, density, or mass. They vary greatly in size or quantity, from subatomic particles like the electron, to microscopic particles like atoms and molecules, to macroscopic particles like powders and other granular materials. Particles can also be used to create scientific models of even larger objects depending on their density, such as humans moving in a crowd or celestial bodies in motion. The term ''particle'' is rather general in meaning, and is refined as needed by various scientific fields. Anything that is composed of particles may be referred to as being particulate. However, the noun '' particulate'' is most frequently used to refer to pollutants in the Earth's atmosphere, which are a suspension of unconnected particles, rather than a connected particle aggregation. Conceptual properties ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
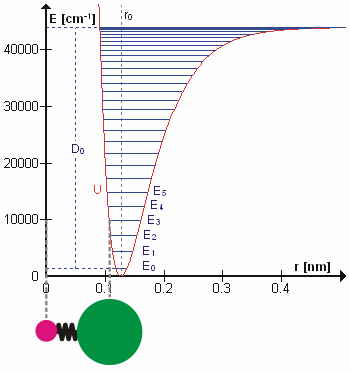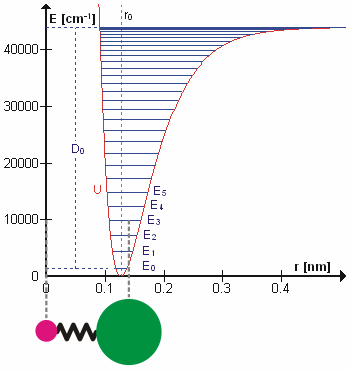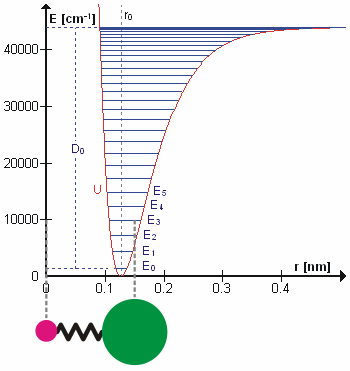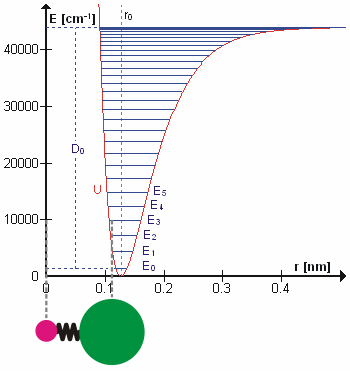 |
Molecular Vibration
A molecular vibration is a Periodic function, periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The infrared spectroscopy correlation table, typical vibrational frequencies range from less than 1013 hertz, Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 μm. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of parts of the molecule. In general, a non-linear molecule with ''N'' atoms has vibrational mode, normal modes of vibration, but a ''linear'' molecule has modes, because rotation about the molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration, since it can only stretch or compress the single bond. A molecular vibration is excited when the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Small-angle Approximation
For small angles, the trigonometric functions sine, cosine, and tangent can be calculated with reasonable accuracy by the following simple approximations: : \begin \sin \theta &\approx \tan \theta \approx \theta, \\ mu\cos \theta &\approx 1 - \tfrac12\theta^2 \approx 1, \end provided the angle is measured in radians. Angles measured in degrees must first be converted to radians by multiplying them by . These approximations have a wide range of uses in branches of physics and engineering, including mechanics, electromagnetism, optics, cartography, astronomy, and computer science. One reason for this is that they can greatly simplify differential equations that do not need to be answered with absolute precision. There are a number of ways to demonstrate the validity of the small-angle approximations. The most direct method is to truncate the Maclaurin series for each of the trigonometric functions. Depending on the order of the approximation, \textstyle \cos \theta is approxi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |