 |
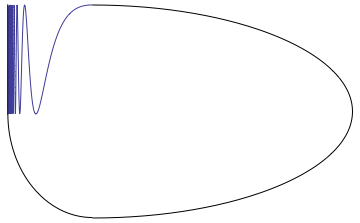
Shape Theory (mathematics)
Shape theory is a branch of topology that provides a more global view of the topological spaces than homotopy theory. The two coincide on compacta dominated homotopically by finite polyhedra. Shape theory associates with the Čech homology theory while homotopy theory associates with the singular homology theory. Background Shape theory was invented and published by D. E. Christie in 1944; it was reinvented, further developed and promoted by the Polish mathematician Karol Borsuk in 1968. Actually, the name ''shape theory'' was coined by Borsuk. Warsaw circle Borsuk lived and worked in Warsaw, hence the name of one of the fundamental examples of the area, the Warsaw circle. . Math 205B-2012 Lecture Notes, University of California Riverside. Retrieved ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Torsion (mechanics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a Set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of List of continuity-related mathematical topics, continuity. Euclidean spaces, and, more generally, metric spaces are examples of topological spaces, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and Homotopy, homotopies. A property that is invariant under such deformations is a to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Fundamenta Mathematicae
''Fundamenta Mathematicae'' is a peer-reviewed scientific journal of mathematics with a special focus on the foundations of mathematics, concentrating on set theory, mathematical logic, topology and its interactions with algebra, and dynamical systems. The first specialized journal in the field of mathematics, originally it covered only topology, set theory, and foundations of mathematics..... It is published by the Mathematics Institute of the Polish Academy of Sciences. History The journal was conceived by Zygmunt Janiszewski as a means to foster mathematical research in Poland.According to and to the introduction to the 100th volume of the journal (1978, pp=1–2). These two sources cite an article written by Janiszewski himself in 1918 and titled "''On the needs of Mathematics in Poland''". Janiszewski posited that, to achieve its goal, the journal should not compel Polish mathematicians to submit articles written exclusively in Polish, and should be devoted only to a sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Springer Science+Business Media
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second-largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Lecture Notes In Mathematics
''Lecture Notes in Mathematics'' is a book series in the field of mathematics, including articles related to both research and teaching. It was established in 1964 and was edited by A. Dold, Heidelberg and B. Eckmann, Zürich. Its publisher is Springer Science+Business Media (formerly Springer-Verlag). The intent of the series is to publish not only lecture notes, but results from seminars and conferences, more quickly than the several-years-long process of publishing polished journal papers in mathematics. In order to speed the publication process, early volumes of the series (before electronic publishing) were reproduced photographically from typewritten manuscripts. According to Earl Taft, it has been "enormously successful" and "is considered a very valuable service to the mathematical community". As of 2023, there has been over 2300 volumes in the series. See also * ''Lecture Notes in Physics'' * ''Lecture Notes in Computer Science ''Lecture Notes in Computer Science'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Rocky Mountain Journal Of Mathematics
'' The Rocky Mountain Journal of Mathematics'' is a peer-reviewed mathematics journal published by the Rocky Mountain Mathematics Consortium. Founded in 1971, the journal publishes both research and expository articles on mathematics, with an emphasis on survey articles. The journal is indexed by ''Mathematical Reviews'' and Zentralblatt MATH. Its 2009 MCQ was 0.25. According to the ''Journal Citation Reports'', the journal has a 2016 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 0.250. References External links * Mathematics journals Academic journals established in 1971 English-language journals Bimonthly journals Academic journals published by learned and professional societies {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Mathematical Proceedings Of The Cambridge Philosophical Society
''Mathematical Proceedings of the Cambridge Philosophical Society'' is a mathematical journal published by Cambridge University Press for the Cambridge Philosophical Society. It aims to publish original research papers from a wide range of pure and applied mathematics. The journal, titled ''Proceedings of the Cambridge Philosophical Society'' before 1975, has been published since 1843. Abstracting and indexing The journal is abstracted and indexed in *MathSciNet *Science Citation Index Expanded *Scopus *ZbMATH Open See also *Cambridge Philosophical Society The Cambridge Philosophical Society (CPS) is a scientific society at the University of Cambridge. It was founded in 1819. The name derives from the medieval use of the word philosophy to denote any research undertaken outside the fields of law ... External linksofficial website References Academic journals associated with learned and professional societies Cambridge University Press academic journals Mathematics e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Peter Hilton
Peter John Hilton (7 April 1923Peter Hilton, "On all Sorts of Automorphisms", ''The American Mathematical Monthly'', 92(9), November 1985, p. 6506 November 2010) was a British mathematician, noted for his contributions to homotopy theory and for code-breaking during World War II. Early life He was born in Brondesbury, London, the son of Mortimer Jacob Hilton (1893–1959), a Jewish physician who was in general practice in Peckham, and his wife Elizabeth Amelia Freedman (1900–1984), and was brought up in Kilburn. The physiologist Sidney Montague Hilton (1921–2011) of the University of Birmingham Medical School was his elder brother. Hilton was educated at St Paul's School, London."About the speaker"announcement of a lecture given by Peter Hilton at Bletchley Park on 12 July 2006. Retrieved 18 January 2007. He went to The Queen's College, Oxford in 1940 to read mathematics, on an open scholarship, where the mathematics tutor was Ughtred Haslam-Jones. Bletchley Park A war ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Simon & Schuster
Simon & Schuster LLC (, ) is an American publishing house owned by Kohlberg Kravis Roberts since 2023. It was founded in New York City in 1924, by Richard L. Simon and M. Lincoln Schuster. Along with Penguin Random House, Hachette Book Group USA, Hachette, HarperCollins and Macmillan Publishers, Simon & Schuster is considered one of the Big Five (publishers), 'Big Five' English language publishers. , Simon & Schuster was the third largest publisher in the United States, publishing 2,000 titles annually under 35 different Imprint (trade name), imprints. History Early years In 1924, Richard L. Simon, Richard Simon's aunt, a crossword puzzle enthusiast, asked whether there was a book of ''New York World'' crossword puzzles, which were popular at the time. After discovering that none had been published, Simon and M. Lincoln Schuster, Max Schuster decided to launch a company to exploit the opportunity.Frederick Lewis Allen, ''Only Yesterday: An Informal History of the 1920s'', p. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
List Of Topologies
The following is a list of named topologies or topological spaces, many of which are counterexamples in topology and related branches of mathematics. This is not a list of properties that a topology or topological space might possess; for that, see List of general topology topics and Topological property. Discrete and indiscrete * Discrete topology − All subsets are open. * Indiscrete topology, chaotic topology, or Trivial topology − Only the empty set and its complement are open. Cardinality and ordinals * Cocountable topology ** Given a topological space (X, \tau), the '' '' on X is the topology having as a subbasis the union of and the family of all subsets of X whose complements in X are countable. * Cofinite topology * Double-pointed cofinite topology * Ordinal number topology * Pseudo-arc * Ran space * Tychonoff plank Finite spaces * Discrete two-point space − The simplest example of a totally disconnected discrete space. * Finite topological space * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Operator Algebra
In functional analysis, a branch of mathematics, an operator algebra is an algebra of continuous linear operators on a topological vector space, with the multiplication given by the composition of mappings. The results obtained in the study of operator algebras are often phrased in algebraic terms, while the techniques used are often highly analytic.''Theory of Operator Algebras I'' By Masamichi Takesaki, Springer 2012, p vi Although the study of operator algebras is usually classified as a branch of functional analysis, it has direct applications to representation theory, differential geometry, quantum statistical mechanics, quantum information, and quantum field theory. Overview Operator algebras can be used to study arbitrary sets of operators with little algebraic relation ''simultaneously''. From this point of view, operator algebras can be regarded as a generalization of spectral theory of a single operator. In general, operator algebras are non-commutative ring ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Noncommutative Geometry
Noncommutative geometry (NCG) is a branch of mathematics concerned with a geometric approach to noncommutative algebras, and with the construction of ''spaces'' that are locally presented by noncommutative algebras of functions, possibly in some generalized sense. A noncommutative algebra is an associative algebra in which the multiplication is not commutative, that is, for which xy does not always equal yx; or more generally an algebraic structure in which one of the principal binary operations is not commutative; one also allows additional structures, e.g. topology or norm, to be possibly carried by the noncommutative algebra of functions. An approach giving deep insight about noncommutative spaces is through operator algebras, that is, algebras of bounded linear operators on a Hilbert space. Perhaps one of the typical examples of a noncommutative space is the " noncommutative torus", which played a key role in the early development of this field in 1980s and lead to noncomm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |