|
Seismic Trace
In seismology, a seismic trace is the recorded curve from a single seismograph when measuring ground movement. The name comes from the curve plotted by a seismograph as the paper roll rotated and the needle left a trace from which information about the subsurface could be extracted. Today's instruments record the data digitally and the word trace has come to mean the digital curve. Complex seismic trace The recorded seismic trace is considered the real part of the complex trace. By phase shifting the recorded trace by 90 degrees, we can obtain the imaginary part of the complex trace. The complex seismic trace is a complex function whose real and imaginary part are the previously mentioned. From the complex trace, one can now define seismic attribute In reflection seismology, a seismic attribute is a quantity extracted or derived from seismic data that can be analysed in order to enhance information that might be more subtle in a traditional seismic image, leading to a better geo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismology
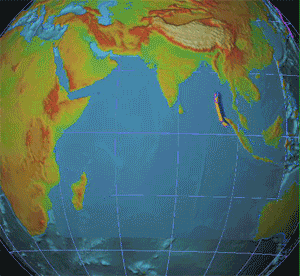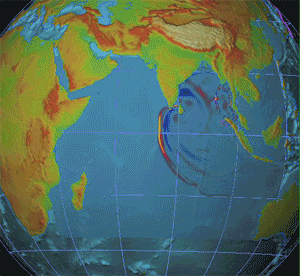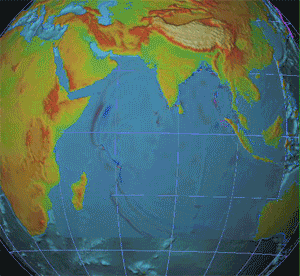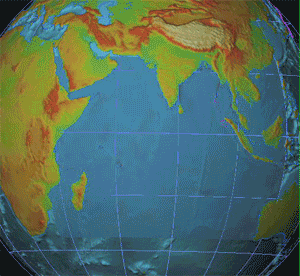
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes (or generally, quakes) and the generation and propagation of elastic waves through planetary bodies. It also includes studies of the environmental effects of earthquakes such as tsunamis; other seismic sources such as volcanoes, plate tectonics, glaciers, rivers, oceanic microseisms, and the atmosphere; and artificial processes such as explosions. Paleoseismology is a related field that uses geology to infer information regarding past earthquakes. A recording of Earth's motion as a function of time, created by a seismograph is called a seismogram. A seismologist is a scientist who works in basic or applied seismology. History Scholarly interest in earthquakes can be traced back to antiquity. Early speculations on the natural causes of earthquakes were included in the writings of Thales of Miletu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismometer
A seismometer is an instrument that responds to ground displacement and shaking such as caused by quakes, volcanic eruptions, and explosions. They are usually combined with a timing device and a recording device to form a seismograph. The output of such a device—formerly recorded on paper (see picture) or film, now recorded and processed digitally—is a ''seismogram''. Such data is used to locate and characterize earthquakes, and to study the internal structure of Earth. Basic principles A simple seismometer, sensitive to up-down motions of the Earth, is like a weight hanging from a spring, both suspended from a frame that moves along with any motion detected. The relative motion between the weight (called the mass) and the frame provides a measurement of the vertical ground motion. A rotating drum is attached to the frame and a pen is attached to the weight, thus recording any ground motion in a seismogram. Any movement from the ground moves the frame. The mass tends ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imaginary Number
An imaginary number is the product of a real number and the imaginary unit , is usually used in engineering contexts where has other meanings (such as electrical current) which is defined by its property . The square (algebra), square of an imaginary number is . For example, is an imaginary number, and its square is . The number 0, zero is considered to be both real and imaginary. Originally coined in the 17th century by René Descartes as a derogatory term and regarded as fictitious or useless, the concept gained wide acceptance following the work of Leonhard Euler (in the 18th century) and Augustin-Louis Cauchy and Carl Friedrich Gauss (in the early 19th century). An imaginary number can be added to a real number to form a complex number of the form , where the real numbers and are called, respectively, the ''real part'' and the ''imaginary part'' of the complex number. History Although the Greek mathematician and engineer Heron of Alexandria is noted as the first t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Function
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, and applied mathematics, as well as in physics, including the branches of hydrodynamics, thermodynamics, quantum mechanics, and twistor theory. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to the sum function given by its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable, that is, ''holomorphic functions''. The concept can be extended to functions of several complex variables. Complex analysis is contrasted with real analysis, which deals with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismic Attribute
In reflection seismology, a seismic attribute is a quantity extracted or derived from seismic data that can be analysed in order to enhance information that might be more subtle in a traditional seismic image, leading to a better geological or geophysical interpretation of the data. Examples of seismic attributes can include measured time, amplitude, frequency and attenuation, in addition to combinations of these. Most seismic attributes are post-stack, but those that use CMP gathers, such as amplitude versus offset (AVO), must be analysed pre-stack.Young, R. & LoPiccolo, R. 2005. AVO analysis demystified. E&P. http://www.e-seis.com/white_papers/AVO%20Analysis%20Demystified.pdf They can be measured along a single seismic trace or across multiple traces within a defined window. The first attributes developed were related to the 1D complex seismic trace and included: envelope amplitude, instantaneous phase, instantaneous frequency, and apparent polarity. Acoustic impedance o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismology Measurement
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes (or generally, quakes) and the generation and propagation of elastic waves through planetary bodies. It also includes studies of the environmental effects of earthquakes such as tsunamis; other seismic sources such as volcanoes, plate tectonics, glaciers, rivers, oceanic microseisms, and the atmosphere; and artificial processes such as explosions. Paleoseismology is a related field that uses geology to infer information regarding past earthquakes. A recording of Earth's motion as a function of time, created by a seismograph is called a seismogram. A seismologist is a scientist who works in basic or applied seismology. History Scholarly interest in earthquakes can be traced back to antiquity. Early speculations on the natural causes of earthquakes were included in the writings of Thales of Miletus (), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |