 |
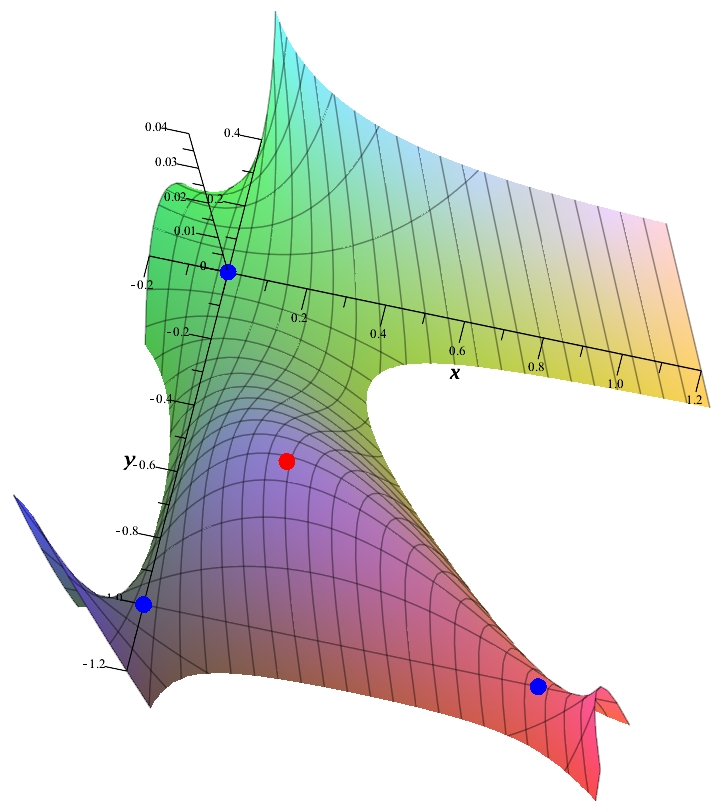
Second Partial Derivative Test
In mathematics, the second partial derivative test is a method in multivariable calculus used to determine if a Critical point (mathematics), critical point of a function is a maxima and minima, local minimum, maximum or saddle point. Functions of two variables Suppose that is a differentiable real function of two variables whose second partial derivatives exist and are continuous function, continuous. The Hessian matrix of is the 2 × 2 matrix of partial derivatives of : H(x,y) = \begin f_(x,y) &f_(x,y)\\ f_(x,y) &f_(x,y) \end. Define to be the determinant D(x,y)=\det(H(x,y)) = f_(x,y)f_(x,y) - \left( f_(x,y) \right)^2 of . Finally, suppose that is a critical point of , that is, that . Then the second partial derivative test asserts the following: #If and then is a local minimum of . #If and then is a local maximum of . #If then is a saddle point of . #If then the point could be any of a minimum, maximum, or saddle point (that is, the test is inconclusive). S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Second Partial Derivative Test
In mathematics, the second partial derivative test is a method in multivariable calculus used to determine if a Critical point (mathematics), critical point of a function is a maxima and minima, local minimum, maximum or saddle point. Functions of two variables Suppose that is a differentiable real function of two variables whose second partial derivatives exist and are continuous function, continuous. The Hessian matrix of is the 2 × 2 matrix of partial derivatives of : H(x,y) = \begin f_(x,y) &f_(x,y)\\ f_(x,y) &f_(x,y) \end. Define to be the determinant D(x,y)=\det(H(x,y)) = f_(x,y)f_(x,y) - \left( f_(x,y) \right)^2 of . Finally, suppose that is a critical point of , that is, that . Then the second partial derivative test asserts the following: #If and then is a local minimum of . #If and then is a local maximum of . #If then is a saddle point of . #If then the point could be any of a minimum, maximum, or saddle point (that is, the test is inconclusive). S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Sylvester's Criterion
In mathematics, Sylvester’s criterion is a necessary and sufficient condition, necessary and sufficient criterion to determine whether a Hermitian matrix is Definite matrix, positive-definite. Sylvester's criterion states that a ''n'' × ''n'' Hermitian matrix ''M'' is positive-definite if and only if all the following matrices have a positive determinant: * the upper left 1-by-1 corner of ''M'', * the upper left 2-by-2 corner of ''M'', * the upper left 3-by-3 corner of ''M'', * \quad\vdots * ''M'' itself. In other words, all of the ''leading'' principal minors must be positive. By using appropriate permutations of rows and columns of ''M'', it can also be shown that the positivity of ''any'' nested sequence of ''n'' principal minors of ''M'' is equivalent to ''M'' being positive-definite. An analogous theorem holds for characterizing positive-semidefinite matrix, positive-semidefinite Hermitian matrices, except that it is no longer sufficient to consider only the ''leading'' pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Minor (linear Algebra)
In linear algebra, a minor of a matrix (mathematics), matrix is the determinant of some smaller square matrix generated from by removing one or more of its rows and columns. Minors obtained by removing just one row and one column from square matrices (first minors) are required for calculating matrix cofactors, which are useful for computing both the determinant and Inverse matrix, inverse of square matrices. The requirement that the square matrix be smaller than the original matrix is often omitted in the definition. Definition and illustration First minors If is a square matrix, then the ''minor'' of the entry in the -th row and -th column (also called the ''minor'', or a ''first minor'') is the determinant of the submatrix formed by deleting the -th row and -th column. This number is often denoted . The ''cofactor'' is obtained by multiplying the minor by . To illustrate these definitions, consider the following matrix, \begin 1 & 4 & 7 \\ 3 & 0 & 5 \\ -1 & 9 & 11 \\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Second Derivative Test
In calculus, a derivative test uses the derivatives of a function to locate the critical points of a function and determine whether each point is a local maximum, a local minimum, or a saddle point. Derivative tests can also give information about the concavity of a function. The usefulness of derivatives to find extrema is proved mathematically by Fermat's theorem of stationary points. First-derivative test The first-derivative test examines a function's monotonic properties (where the function is increasing or decreasing), focusing on a particular point in its domain. If the function "switches" from increasing to decreasing at the point, then the function will achieve a highest value at that point. Similarly, if the function "switches" from decreasing to increasing at the point, then it will achieve a least value at that point. If the function fails to "switch" and remains increasing or remains decreasing, then no highest or least value is achieved. One can examine a funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Positive-definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Invertible Matrix
In linear algebra, an invertible matrix (''non-singular'', ''non-degenarate'' or ''regular'') is a square matrix that has an inverse. In other words, if some other matrix is multiplied by the invertible matrix, the result can be multiplied by an inverse to undo the operation. An invertible matrix multiplied by its inverse yields the identity matrix. Invertible matrices are the same size as their inverse. Definition An -by- square matrix is called invertible if there exists an -by- square matrix such that\mathbf = \mathbf = \mathbf_n ,where denotes the -by- identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix is uniquely determined by , and is called the (multiplicative) ''inverse'' of , denoted by . Matrix inversion is the process of finding the matrix which when multiplied by the original matrix gives the identity matrix. Over a field, a square matrix that is ''not'' invertible is called singular or deg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the matrix and the linear map represented, on a given basis (linear algebra), basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible matrix, invertible and the corresponding linear map is an linear isomorphism, isomorphism. However, if the determinant is zero, the matrix is referred to as singular, meaning it does not have an inverse. The determinant is completely determined by the two following properties: the determinant of a product of matrices is the product of their determinants, and the determinant of a triangular matrix is the product of its diagonal entries. The determinant of a matrix is :\begin a & b\\c & d \end=ad-bc, and the determinant of a matrix is : \begin a & b & c \\ d & e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Multivariable Calculus
Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to calculus with functions of several variables: the differentiation and integration of functions involving multiple variables ('' multivariate''), rather than just one. Multivariable calculus may be thought of as an elementary part of calculus on Euclidean space. The special case of calculus in three dimensional space is often called ''vector calculus''. Introduction In single-variable calculus, operations like differentiation and integration are made to functions of a single variable. In multivariate calculus, it is required to generalize these to multiple variables, and the domain is therefore multi-dimensional. Care is therefore required in these generalizations, because of two key differences between 1D and higher dimensional spaces: # There are infinite ways to approach a single point in higher dimensions, as opposed to two (from the positive and negative direct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Hessian Matrix
In mathematics, the Hessian matrix, Hessian or (less commonly) Hesse matrix is a square matrix of second-order partial derivatives of a scalar-valued Function (mathematics), function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Otto Hesse, Ludwig Otto Hesse and later named after him. Hesse originally used the term "functional determinants". The Hessian is sometimes denoted by H or \nabla\nabla or \nabla^2 or \nabla\otimes\nabla or D^2. Definitions and properties Suppose f : \R^n \to \R is a function taking as input a vector \mathbf \in \R^n and outputting a scalar f(\mathbf) \in \R. If all second-order partial derivatives of f exist, then the Hessian matrix \mathbf of f is a square n \times n matrix, usually defined and arranged as \mathbf H_f= \begin \dfrac & \dfrac & \cdots & \dfrac \\[2.2ex] \dfrac & \dfrac & \cdots & \dfrac \\[2.2ex] \vdots & \vdot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |