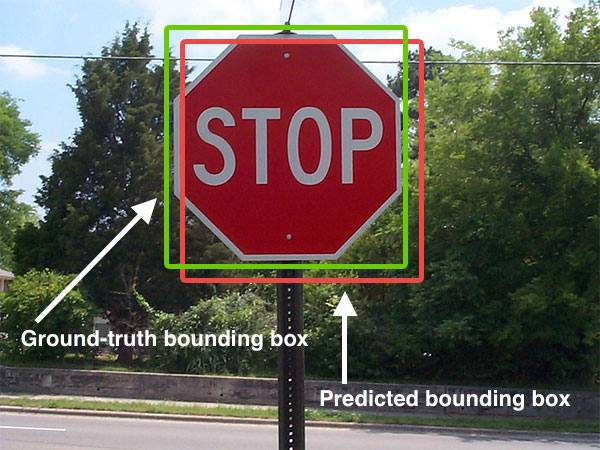
|
Scale-invariant Feature Transform
The scale-invariant feature transform (SIFT) is a computer vision algorithm to detect, describe, and match local '' features'' in images, invented by David Lowe in 1999. Applications include object recognition, robotic mapping and navigation, image stitching, 3D modeling, gesture recognition, video tracking, individual identification of wildlife and match moving. SIFT keypoints of objects are first extracted from a set of reference images and stored in a database. An object is recognized in a new image by individually comparing each feature from the new image to this database and finding candidate matching features based on Euclidean distance of their feature vectors. From the full set of matches, subsets of keypoints that agree on the object and its location, scale, and orientation in the new image are identified to filter out good matches. The determination of consistent clusters is performed rapidly by using an efficient hash table implementation of the generalised Hough t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the form of decisions. "Understanding" in this context signifies the transformation of visual images (the input to the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scientific discipline of computer vision is concerned with the theory behind artificial systems that extract information from images. Image data can take many forms, such as video sequences, views from multiple cameras, multi-dimensional data from a 3D scanning, 3D scanner, 3D point clouds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difference Of Gaussians
In imaging science, difference of Gaussians (DoG) is a feature enhancement algorithm that involves the subtraction of one Gaussian blurred version of an original image from another, less blurred version of the original. In the simple case of grayscale images, the blurred images are obtained by convolving the original grayscale images with Gaussian kernels having differing width (standard deviations). Blurring an image using a Gaussian kernel suppresses only high-frequency spatial information. Subtracting one image from the other preserves spatial information that lies between the range of frequencies that are preserved in the two blurred images. Thus, the DoG is a spatial band-pass filter that attenuates frequencies in the original grayscale image that are far from the band center. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nearest Neighbor Search
Nearest neighbor search (NNS), as a form of proximity search, is the optimization problem of finding the point in a given set that is closest (or most similar) to a given point. Closeness is typically expressed in terms of a dissimilarity function: the less similar the objects, the larger the function values. Formally, the nearest-neighbor (NN) search problem is defined as follows: given a set ''S'' of points in a space ''M'' and a query point ''q'' ∈ ''M'', find the closest point in ''S'' to ''q''. Donald Knuth in vol. 3 of '' The Art of Computer Programming'' (1973) called it the post-office problem, referring to an application of assigning to a residence the nearest post office. A direct generalization of this problem is a ''k''-NN search, where we need to find the ''k'' closest points. Most commonly ''M'' is a metric space and dissimilarity is expressed as a distance metric, which is symmetric and satisfies the triangle inequality. Even more common, ''M'' is take ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Space
Scale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision. It is a formal theory for handling image structures at different scales, by representing an image as a one-parameter family of smoothed images, the scale-space representation, parametrized by the size of the smoothing kernel used for suppressing fine-scale structures. The parameter t in this family is referred to as the ''scale parameter'', with the interpretation that image structures of spatial size smaller than about \sqrt have largely been smoothed away in the scale-space level at scale t. The main type of scale space is the ''linear (Gaussian) scale space'', which has wide applicability as well as the attractive property of being possible to derive from a small set of '' scale-space axioms''. The corresponding scale-space framework encompasses a th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difference Of Gaussians
In imaging science, difference of Gaussians (DoG) is a feature enhancement algorithm that involves the subtraction of one Gaussian blurred version of an original image from another, less blurred version of the original. In the simple case of grayscale images, the blurred images are obtained by convolving the original grayscale images with Gaussian kernels having differing width (standard deviations). Blurring an image using a Gaussian kernel suppresses only high-frequency spatial information. Subtracting one image from the other preserves spatial information that lies between the range of frequencies that are preserved in the two blurred images. Thus, the DoG is a spatial band-pass filter that attenuates frequencies in the original grayscale image that are far from the band center. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primary Visual Cortex
The visual cortex of the brain is the area of the cerebral cortex that processes visual information. It is located in the occipital lobe. Sensory input originating from the eyes travels through the lateral geniculate nucleus in the thalamus and then reaches the visual cortex. The area of the visual cortex that receives the sensory input from the lateral geniculate nucleus is the primary visual cortex, also known as visual area 1 ( V1), Brodmann area 17, or the striate cortex. The extrastriate areas consist of visual areas 2, 3, 4, and 5 (also known as V2, V3, V4, and V5, or Brodmann area 18 and all Brodmann area 19). Both hemispheres of the brain include a visual cortex; the visual cortex in the left hemisphere receives signals from the right visual field, and the visual cortex in the right hemisphere receives signals from the left visual field. Introduction The primary visual cortex (V1) is located in and around the calcarine fissure in the occipital lobe. Each hemi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-d Tree
In computer science, a ''k''-d tree (short for ''k-dimensional tree'') is a space-partitioning data structure for organizing points in a ''k''-dimensional space. K-dimensional is that which concerns exactly k orthogonal axes or a space of any number of dimensions. ''k''-d trees are a useful data structure for several applications, such as: * Searches involving a multidimensional search key (e.g. range searches and nearest neighbor searches) & * Creating point clouds. ''k''-d trees are a special case of binary space partitioning trees. Description The ''k''-d tree is a binary tree in which ''every'' node is a ''k''-dimensional point. Every non-leaf node can be thought of as implicitly generating a splitting hyperplane that divides the space into two parts, known as half-spaces. Points to the left of this hyperplane are represented by the left subtree of that node and points to the right of the hyperplane are represented by the right subtree. The hyperplane direction is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Probability
Bayesian probability ( or ) is an interpretation of the concept of probability, in which, instead of frequency or propensity of some phenomenon, probability is interpreted as reasonable expectation representing a state of knowledge or as quantification of a personal belief. The Bayesian interpretation of probability can be seen as an extension of propositional logic that enables reasoning with hypotheses; that is, with propositions whose truth or falsity is unknown. In the Bayesian view, a probability is assigned to a hypothesis, whereas under frequentist inference, a hypothesis is typically tested without being assigned a probability. Bayesian probability belongs to the category of evidential probabilities; to evaluate the probability of a hypothesis, the Bayesian probabilist specifies a prior probability. This, in turn, is then updated to a posterior probability in the light of new, relevant data (evidence). The Bayesian interpretation provides a standard set of procedur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Least Squares
Linear least squares (LLS) is the least squares approximation of linear functions to data. It is a set of formulations for solving statistical problems involved in linear regression, including variants for ordinary (unweighted), weighted, and generalized (correlated) residuals. Numerical methods for linear least squares include inverting the matrix of the normal equations and orthogonal decomposition methods. Basic formulation Consider the linear equation where A \in \mathbb^ and b \in \mathbb^m are given and x \in \mathbb^n is variable to be computed. When m > n, it is generally the case that () has no solution. For example, there is no value of x that satisfies \begin 1 & 0 \\ 0 & 1 \\ 1 & 1 \end x = \begin 1 \\ 1 \\ 0 \end, because the first two rows require that x = (1, 1), but then the third row is not satisfied. Thus, for m > n, the goal of solving () exactly is typically replaced by finding the value of x that minimizes some error. There are many ways th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hough Transform
The Hough transform () is a feature extraction technique used in image analysis, computer vision, pattern recognition, and digital image processing. The purpose of the technique is to find imperfect instances of objects within a certain class of shapes by a voting procedure. This voting procedure is carried out in a parameter space, from which object candidates are obtained as local maxima in a so-called accumulator space that is explicitly constructed by the algorithm for computing the Hough transform. Mathematically it is simply the Radon transform in the plane, known since at least 1917, but the Hough transform refers to its use in image analysis. The classical Hough transform was concerned with the identification of Line (mathematics), lines in the image, but later the Hough transform has been extended to identifying positions of arbitrary shapes, most commonly circles or ellipses. The Hough transform as it is universally used today was invented by Richard Duda and Peter E. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |