|
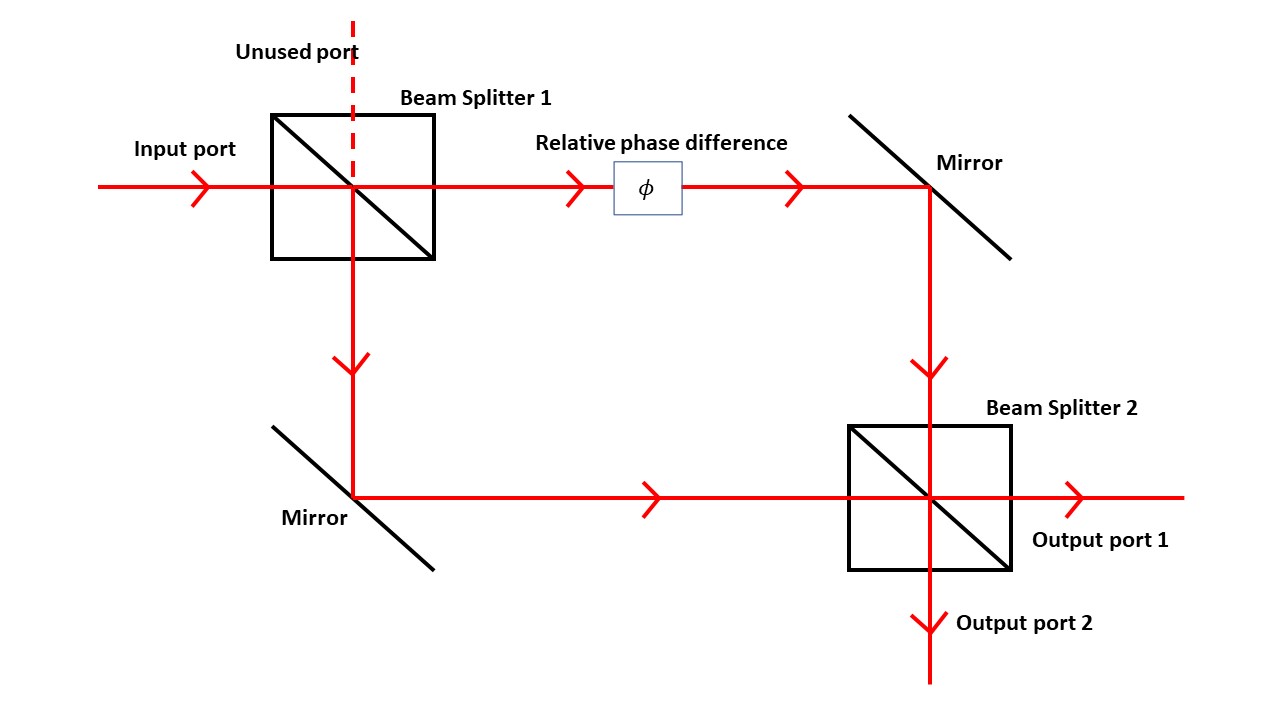
SU(1,1) Interferometry
SU(1,1) interferometry is a technique that uses Optical parametric amplifier, parametric amplification for splitting and mixing of electromagnetic waves for precise estimation of phase change and achieves the Uncertainty principle, Heisenberg limit of sensitivity with fewer optical elements than Interferometry, conventional interferometric techniques. Introduction Interferometry is an important technique in the field of optics that have been utilised for fundamental proof of principles experiments and in the development of new technologies. This technique, primarily based on the interference of Electromagnetic radiation, electromagnetic waves, has been widely explored in the field of quantum metrology and precision measurements for achieving sensitivity in measurements beyond what is possible with classical methods and resources. Interferometry is a desired platform for precise estimation of physical quantities because of its ability to sense small phase changes. One of the most pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Parametric Amplifier
An optical parametric amplifier, abbreviated OPA, is a laser light source that emits light of variable wavelengths by an optical parametric amplification process. It is essentially the same as an optical parametric oscillator, but without the optical cavity (i.e., the light beams pass through the apparatus just once or twice, rather than many many times). Optical parametric generation (OPG) Optical parametric generation (OPG) (also called "optical parametric fluorescence", or " spontaneous parametric down conversion") often precedes optical parametric amplification. In optical parametric generation, the input is one light beam of frequency ωp, and the output is two light beams of lower frequencies ωs and ωi, with the requirement ωp=ωs+ωi. These two lower-frequency beams are called the "signal" and "idler", respectively. This light emission is based on the nonlinear optical principle. The photon of an incident laser pulse (pump) is, by a nonlinear optical crystal, divide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NOON State
In quantum optics, a NOON state or N00N state is a quantum-mechanical many-body entangled state: : , \text \rangle = \frac, \, which represents a superposition of ''N'' particles in mode ''a'' with zero particles in mode ''b'', and vice versa. Usually, the particles are photons, but in principle any bosonic field can support NOON states. Applications NOON states are an important concept in quantum metrology and quantum sensing for their ability to make precision phase measurements when used in an optical interferometer. For example, consider the observable : A = , N,0\rangle\langle 0,N, + , 0,N\rangle\langle N,0, . \, The expectation value of A for a system in a NOON state switches between +1 and −1 when \theta changes from 0 to \pi/N. Moreover, the error in the phase measurement becomes : \Delta \theta = \frac = \frac. This is the so-called Heisenberg limit, and gives a quadratic improvement over the standard quantum limit. NOON states are closely rel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interferometric Visibility
The interferometric visibility (also known as interference visibility and fringe visibility, or just visibility when in context) is a measure of the contrast of ''interference'' in any system subject to wave superposition. Examples include as optics, quantum mechanics, water waves, sound waves, or electrical signals. Visibility is defined as the ratio of the amplitude of the interference pattern to the sum of the powers of the individual waves. The interferometric visibility gives a practical way to measure the coherence of two waves (or one wave with itself). A theoretical definition of the coherence is given by the degree of coherence, using the notion of correlation. Generally, two or more waves are superimposed and as the phase difference between them varies, the power or intensity (probability or population in quantum mechanics) of the resulting wave oscillates, forming an interference pattern. The pointwise definition may be expanded to a visibility function varying over ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coherent State
In physics, specifically in quantum mechanics, a coherent state is the specific quantum state of the quantum harmonic oscillator, often described as a state that has dynamics most closely resembling the oscillatory behavior of a classical harmonic oscillator. It was the first example of quantum dynamics when Erwin Schrödinger derived it in 1926, while searching for solutions of the Schrödinger equation that satisfy the correspondence principle. The quantum harmonic oscillator (and hence the coherent states) arise in the quantum theory of a wide range of physical systems.J.R. Klauder and B. Skagerstam, ''Coherent States'', World Scientific, Singapore, 1985. For instance, a coherent state describes the oscillating motion of a particle confined in a quadratic potential well (for an early reference, see e.g. Schiff's textbook). The coherent state describes a state in a system for which the ground-state wavepacket is displaced from the origin of the system. This state can be relate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Creation And Annihilation Operators
Creation operators and annihilation operators are Operator (mathematics), mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator (usually denoted \hat) lowers the number of particles in a given state by one. A creation operator (usually denoted \hat^\dagger) increases the number of particles in a given state by one, and it is the Hermitian adjoint, adjoint of the annihilation operator. In many subfields of physics and chemistry, the use of these operators instead of wavefunctions is known as second quantization. They were introduced by Paul Dirac. Creation and annihilation operators can act on states of various types of particles. For example, in quantum chemistry and many-body theory the creation and annihilation operators often act on electron states. They can also refer specifically to the ladder operators for the quantum harmonic oscillator. In the la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. The current standard model of particle physics is based on QFT. History Quantum field theory emerged from the work of generations of theoretical physicists spanning much of the 20th century. Its development began in the 1920s with the description of interactions between light and electrons, culminating in the first quantum field theory—quantum electrodynamics. A major theoretical obstacle soon followed with the appearance and persistence of various infinities in perturbative calculations, a problem only resolved in the 1950s with the invention of the renormalization procedure. A second major barrier came with QFT's apparent inabili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SU(1
SU, Su or su may refer to: Arts and entertainment * Su (Shugo Chara!), a fictional character in the manga series ''Shugo Chara!'' * ''Sinclair User'', a magazine * ''Steven Universe'', an American animated television series on Cartoon Network * StumbleUpon, a web discovery service Businesses and organizations * Aeroflot, a Russian airline (IATA code) * Scripture Union, a Christian organisation * Socialist Youth (Norway), a Norwegian youth league * Sukhoi, a Russian aircraft company Geography * Su, Catalonia, a village in Spain * Su, Iran, a village in Kurdistan Province, Iran * Jiangsu (abbr. Sū, 苏), province of the People's Republic of China ** Suzhou, Jiangsu (abbr. Sū, 苏), city in Jiangsu province * Soviet Union (former ISO country code) * Subotica, a city in Serbia (license plate code SU) Language * Su (kana) * Sú (cuneiform), a sign in cuneiform writing * Sundanese Language, ISO 639-1 code: su Science, technology, and mathematics Computing * .su, country code ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four-wave Mixing
Four-wave mixing (FWM) is an intermodulation phenomenon in nonlinear optics, whereby interactions between two or three wavelengths produce two or one new wavelengths. It is similar to the third-order intercept point in electrical systems. Four-wave mixing can be compared to the intermodulation distortion in standard electrical systems. It is a parametric nonlinear process, in that the energy of the incoming photons is conservation of energy, conserved. FWM is a phase-sensitive process, in that the efficiency of the process is strongly affected by Nonlinear optics#Phase matching, phase matching conditions. Mechanism When three frequencies (f1, f2, and f3) interact in a nonlinear medium, they give rise to a fourth frequency (f4) which is formed by the scattering of the incident photons, producing the fourth photon. Given inputs ''f1, f2,'' and ''f3'', the nonlinear system will produce : \pm f_ \pm f_ \pm f_ From calculations with the three input signals, it is found that 12 inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Optics
Nonlinear optics (NLO) is the branch of optics that describes the behaviour of light in Nonlinearity, nonlinear media, that is, media in which the polarization density P responds non-linearly to the electric field E of the light. The non-linearity is typically observed only at very high light intensities (when the electric field of the light is >108 V/m and thus comparable to the atomic electric field of ~1011 V/m) such as those provided by lasers. Above the Schwinger limit, the vacuum itself is expected to become nonlinear. In nonlinear optics, the superposition principle no longer holds. History The first nonlinear optical effect to be predicted was two-photon absorption, by Maria Goeppert Mayer for her PhD in 1931, but it remained an unexplored theoretical curiosity until 1961 and the almost simultaneous observation of two-photon absorption at Bell Labs and the discovery of second-harmonic generation by Peter Franken ''et al.'' at University of Michigan, both shortly after th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernard Yurke
Bernard Yurke is an American physicist, currently a distinguished research professor at Boise State University and an Elected Fellow of the American Association for the Advancement of Science The American Association for the Advancement of Science (AAAS) is a United States–based international nonprofit with the stated mission of promoting cooperation among scientists, defending scientific freedom, encouraging scientific responsib .... See also * DNA nanotechnology References Year of birth missing (living people) Living people Fellows of the American Association for the Advancement of Science Boise State University faculty 21st-century American physicists DNA nanotechnology people University of Texas at Austin alumni Cornell University alumni Fellows of the American Physical Society {{US-physicist-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SU(1,1)
In mathematics, the special unitary group of degree , denoted , is the Lie group of unitary matrices with determinant 1. The matrices of the more general unitary group may have complex determinants with absolute value 1, rather than real 1 in the special case. The group operation is matrix multiplication. The special unitary group is a normal subgroup of the unitary group , consisting of all unitary matrices. As a compact classical group, is the group that preserves the standard inner product on \mathbb^n. It is itself a subgroup of the general linear group, \operatorname(n) \subset \operatorname(n) \subset \operatorname(n, \mathbb ). The groups find wide application in the Standard Model of particle physics, especially in the electroweak interaction and in quantum chromodynamics. The simplest case, , is the trivial group, having only a single element. The group is isomorphic to the group of quaternions of norm 1, and is thus diffeomorphic to the 3-sphere. Since uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squeezed Coherent State
In physics, a squeezed coherent state is a quantum state that is usually described by two non-commuting observables having continuous spectra of eigenvalues. Examples are position x and momentum p of a particle, and the (dimension-less) electric field in the amplitude X (phase 0) and in the mode Y (phase 90°) of a light wave (the wave's quadratures). The product of the standard deviations of two such operators obeys the uncertainty principle: :\Delta x \Delta p \geq \frac2\; and \;\Delta X \Delta Y \geq \frac4 , respectively. Trivial examples, which are in fact not squeezed, are the ground state , 0\rangle of the quantum harmonic oscillator and the family of coherent states , \alpha\rangle. These states saturate the uncertainty above and have a symmetric distribution of the operator uncertainties with \Delta x_g = \Delta p_g in "natural oscillator units" and \Delta X_g = \Delta Y_g = 1/2. The term squeezed state is actually used for states with a standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |