|
Runcinated 9-demicube
In geometry, runcination is an operation that cuts a regular polytope (or Honeycomb (geometry), honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following Cantellation (geometry), cantellation, and Truncation (geometry), truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become Prism (geometry), p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated Cubic Honeycomb
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol . John Horton Conway called this honeycomb a cubille. Description The cubic honeycomb is a space-filling or three-dimensional tessellation consisting of many cubes that attach each other to the faces; the cube is known as cell of a honeycomb. The parallelepiped is the member of a parallelohedron, generated from three line segments that are not all parallel to a common plane. The cube is the special case of a parallelepiped for having the most symmetric form, generated by three perpendicular unit-length line segments. In three-dimensional space, the cubic honeycomb is the only proper regular space-filling tessellation. It is self-dual. Related honeycombs The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
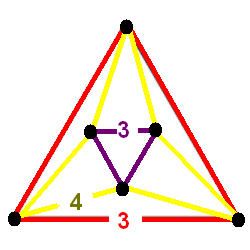
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off. Definitions Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tessellation, tilings or, by extension, to Honeycomb (geometry), space-filling tessellation with polytope Cell (geometry), cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges conn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 120-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Sto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 120-cell
In four-dimensional geometry, a runcinated 120-cell (or ''runcinated 600-cell'') is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 120-cell. There are 4 degrees of runcinations of the 120-cell including with permutations truncations and cantellations. The ''runcinated 120-cell'' can be seen as an Expansion (geometry), expansion applied to a regular 4-polytope, the 120-cell or 600-cell. Runcinated 120-cell The runcinated 120-cell or small disprismatohexacosihecatonicosachoron is a uniform 4-polytope. It has 2640 cells: 120 Dodecahedron, dodecahedra, 720 pentagonal prisms, 1200 triangular prisms, and 600 tetrahedron, tetrahedra. Its vertex figure is a nonuniform triangular antiprism (equilateral-triangular antipodium): its bases represent a dodecahedron and a tetrahedron, and its flanks represent three triangular prisms and three pentagonal prisms. Alternate names * Runcinated 120-cell / Runcinated 600-cell (Norman Johnson (mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 24-cell Schlegel Halfsolid
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Sto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 24-cell
In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 24-cell. There are 3 unique degrees of runcinations of the 24-cell including with permutations truncations and cantellations. Runcinated 24-cell In geometry, the Runcination (geometry), runcinated 24-cell or small prismatotetracontoctachoron is a uniform 4-polytope bounded by 48 octahedron, octahedra and 192 triangular prisms. The octahedral cells correspond with the cells of a 24-cell and its dual. Emanuel Lodewijk Elte, E. L. Elte identified it in 1912 as a semiregular polytope. Alternate names * Runcinated 24-cell (Norman Johnson (mathematician), Norman W. Johnson) * Runcinated icositetrachoron * Runcinated polyoctahedron * Small prismatotetracontoctachoron (spic) (Jonathan Bowers) Coordinates The Cartesian coordinates of the runcinated 24-cell having edge length 2 is given by all permutations of sign and coordinates of: : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schlegel Half-solid Runcinated 8-cell
Schlegel is a German occupational surname. Notable people with the surname include: * Anthony Schlegel (born 1981), American football player * August Wilhelm Schlegel (1767–1845), German poet, brother of Friedrich * Brad Schlegel (born 1968), Canadian ice hockey player * Bernhard Schlegel (born 1951), German-Canadian chemist * Carmela Schlegel (born 1983), Swiss swimmer * Catharina von Schlegel (1697 – after 1768), German hymn writer * Dorothea von Schlegel (1764–1839), German novelist and translator, wife of Friedrich * Elfi Schlegel (born 1964), Canadian gymnast and sportscaster * Frits Schlegel (1896–1965), Danish architect * Gustaaf Schlegel (1840–1903), Dutch sinologist and field naturalist * Hans Schlegel (born 1951), German astronaut * Helmut Schlegel (born 1943), German Franciscan, priest, author, meditation instructor, songwriter * Hermann Schlegel (1804–1884), German ornithologist and herpetologist * Johan Frederik Schlegel (1817–1896), Danish civil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 8-cell Verf
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers. It is a higher order truncation operation, following cantellation, and truncation. It is represented by an extended Schläfli symbol t0,3. This operation only exists for 4-polytopes or higher. This operation is dual-symmetric for regular uniform 4-polytopes and 3-space convex uniform honeycombs. For a regular 4-polytope, the original cells remain, but become separated. The gaps at the separated faces become p-gonal prisms. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become cells. The vertex figure for a regular 4-polytope is an ''q''-gonal antiprism (called an ''antipodium'' if ''p'' and ''r'' are different). For regular 4-polytopes/honeycombs, this operation is also called expansion by Alicia Boole Sto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Runcinated 16-cell
In four-dimensional geometry, a runcinated tesseract (or ''runcinated 16-cell'') is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular tesseract. There are 4 variations of runcinations of the tesseract including with permutations truncations and cantellations. Runcinated tesseract The runcinated tesseract or (small) disprismatotesseractihexadecachoron has 16 tetrahedra, 32 cubes, and 32 triangular prisms. Each vertex is shared by 4 cubes, 3 triangular prisms and one tetrahedron. Construction The runcinated tesseract may be constructed by expanding the cells of a tesseract radially, and filling in the gaps with tetrahedra (vertex figures), cubes (face prisms), and triangular prisms (edge figure prisms). The same process applied to a 16-cell also yields the same figure. Cartesian coordinates The Cartesian coordinates of the vertices of the runcinated tesseract with edge length 2 are all permutations of: :\left(\pm 1,\ \pm 1,\ \pm 1,\ \p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
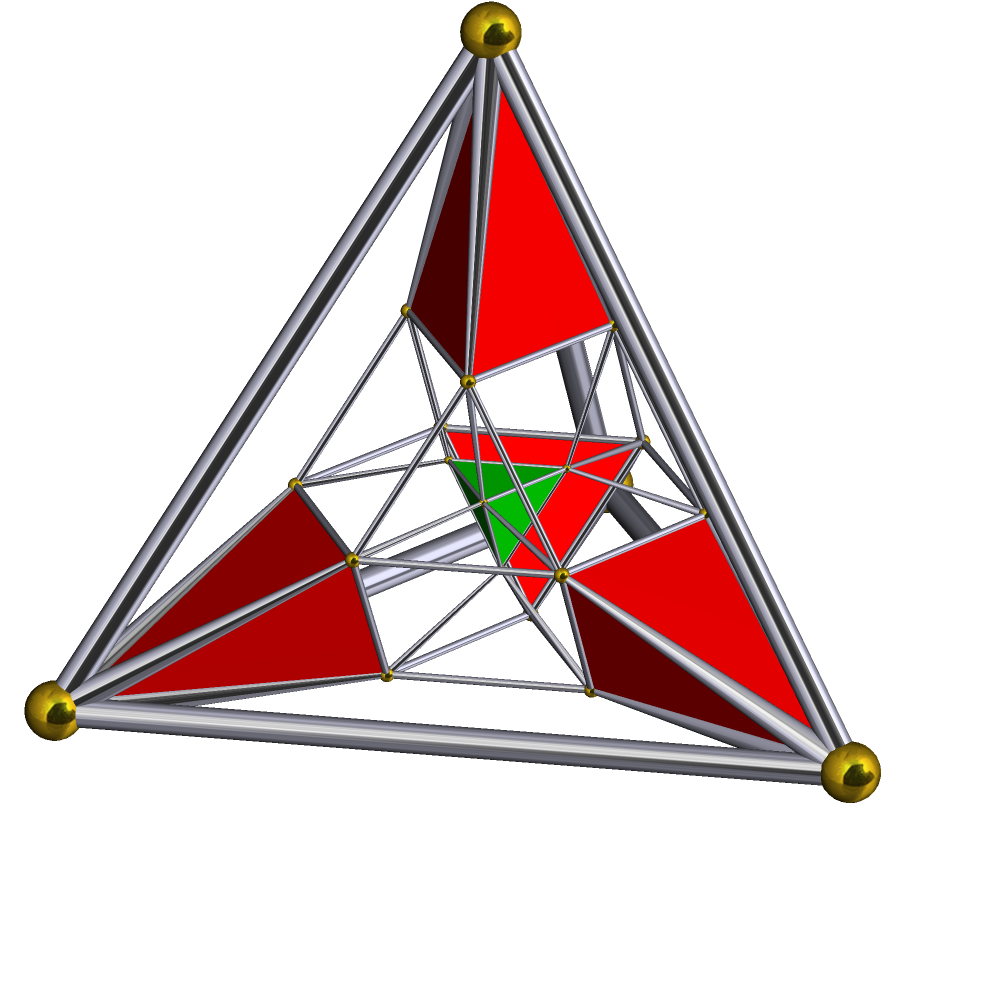
Schlegel Half-solid Runcinated 5-cell
Schlegel is a German occupational surname. Notable people with the surname include: * Anthony Schlegel (born 1981), American football player * August Wilhelm Schlegel (1767–1845), German poet, brother of Friedrich * Brad Schlegel (born 1968), Canadian ice hockey player * Bernhard Schlegel (born 1951), German-Canadian chemist * Carmela Schlegel (born 1983), Swiss swimmer * Catharina von Schlegel (1697 – after 1768), German hymn writer * Dorothea von Schlegel (1764–1839), German novelist and translator, wife of Friedrich * Elfi Schlegel (born 1964), Canadian gymnast and sportscaster * Frits Schlegel (1896–1965), Danish architect * Gustaaf Schlegel (1840–1903), Dutch sinologist and field naturalist * Hans Schlegel (born 1951), German astronaut * Helmut Schlegel (born 1943), German Franciscan, priest, author, meditation instructor, songwriter * Hermann Schlegel (1804–1884), German ornithologist and herpetologist * Johan Frederik Schlegel (1817–1896), Danish civil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |