|
Rotunda (geometry)
In geometry, a rotunda is any member of a family of dihedral-symmetric polyhedra. They are similar to a cupola but instead of alternating squares and triangles, it alternates pentagons and triangles around an axis. The pentagonal rotunda is a Johnson solid In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johns .... Other forms can be generated with dihedral symmetry and distorted equilateral pentagons. Examples Star-rotunda See also * Birotunda References * Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others. * The first proof that there are only 92 Johnson solids. {{Polyhedron navigator Johnson solids ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
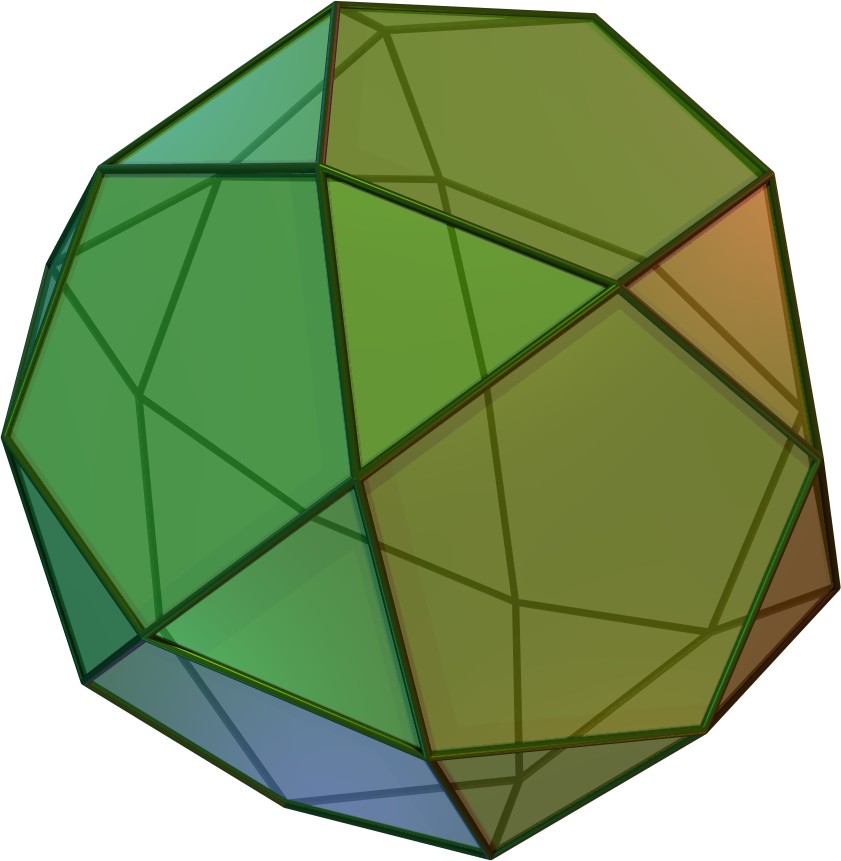
Pentagonal Rotunda
In geometry, the pentagonal rotunda is one of the Johnson solids (). It can be seen as half of an icosidodecahedron, or as half of a pentagonal orthobirotunda. It has a total of 17 faces. Formulae The following formulae for volume, surface area, circumradius, and height are valid if all faces are regular The term regular can mean normal or in accordance with rules. It may refer to: People * Moses Regular (born 1971), America football player Arts, entertainment, and media Music * "Regular" (Badfinger song) * Regular tunings of stringed instrum ..., with edge length ''a'': :V=\left(\frac\left(45+17\sqrt\right)\right)a^3\approx6.91776...a^3 :\begin A&=\left(\frac\sqrt\right)a^2 \\ &=\left(\frac\left(5\sqrt+\sqrt\right)\right)a^2\approx22.3472...a^2 \end :R=\left(\frac\left(1+\sqrt\right)\right)a\approx1.61803...a :H=\left(\sqrt\right)a\approx1.37638...a Dual polyhedron The dual of the pentagonal rotunda has 20 faces: 10 triangular, 5 rhombic, and 5 kites. References E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Rotunda
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification are eith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Birotunda
In geometry, a birotunda is any member of a family of dihedral-symmetric polyhedra, formed from two rotunda adjoined through the largest face. They are similar to a bicupola but instead of alternating squares and triangles, it alternates pentagons and triangles around an axis. There are two forms, ''ortho-'' and ''gyro-'': an ''orthobirotunda'' has one of the two rotundas is placed as the mirror reflection of the other, while in a ''gyrobirotunda'' one rotunda is twisted relative to the other. The pentagonal birotundas can be formed with regular faces, one a Johnson solid, the other a semiregular polyhedron: * pentagonal orthobirotunda, * pentagonal gyrobirotunda, which is also called an icosidodecahedron. Other forms can be generated with dihedral symmetry and distorted equilateral pentagons. Examples See also *Gyroelongated pentagonal birotunda *Elongated pentagonal orthobirotunda *Elongated pentagonal gyrobirotunda In geometry, the elongated pentagonal gyrobirotunda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heptagonal Rotunda
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon. The heptagon is sometimes referred to as the septagon, using "sept-" (an elision of ''septua-'', a Latin-derived numerical prefix, rather than ''hepta-'', a Greek-derived numerical prefix; both are cognate) together with the Greek suffix "-agon" meaning angle. Regular heptagon A regular heptagon, in which all sides and all angles are equal, has internal angles of 5π/7 radians (128 degrees). Its Schläfli symbol is . Area The area (''A'') of a regular heptagon of side length ''a'' is given by: :A = \fraca^2 \cot \frac \simeq 3.634 a^2. This can be seen by subdividing the unit-sided heptagon into seven triangular "pie slices" with vertices at the center and at the heptagon's vertices, and then halving each triangle using the apothem as the common side. The apothem is half the cotangent of \pi/7, and the area of each of the 14 small triangles is one-fourth of the apothem. The area of a regular heptagon i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Green Heptagonal Rotunda
Green is the color between cyan and yellow on the visible spectrum. It is evoked by light which has a dominant wavelength of roughly 495570 nm. In subtractive color systems, used in painting and color printing, it is created by a combination of yellow and cyan; in the RGB color model, used on television and computer screens, it is one of the additive primary colors, along with red and blue, which are mixed in different combinations to create all other colors. By far the largest contributor to green in nature is chlorophyll, the chemical by which plants photosynthesize and convert sunlight into chemical energy. Many creatures have adapted to their green environments by taking on a green hue themselves as camouflage. Several minerals have a green color, including the emerald, which is colored green by its chromium content. During post-classical and early modern Europe, green was the color commonly associated with wealth, merchants, bankers, and the gentry, while red was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Rotunda
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. Regular hexagon A '' regular hexagon'' has Schläfli symbol and can also be constructed as a truncated equilateral triangle, t, which alternates two types of edges. A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle). The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals \tfrac times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has six rotational symmetries (''rotational symmetry of order six'') and six reflection symmetries (''six lines of symmetry''), making up the dihedral group D6. The longest diagonals of a regular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Green Hexagonal Rotunda
Green is the color between cyan and yellow on the visible spectrum. It is evoked by light which has a dominant wavelength of roughly 495570 nm. In subtractive color systems, used in painting and color printing, it is created by a combination of yellow and cyan; in the RGB color model, used on television and computer screens, it is one of the additive primary colors, along with red and blue, which are mixed in different combinations to create all other colors. By far the largest contributor to green in nature is chlorophyll, the chemical by which plants photosynthesize and convert sunlight into chemical energy. Many creatures have adapted to their green environments by taking on a green hue themselves as camouflage. Several minerals have a green color, including the emerald, which is colored green by its chromium content. During post-classical and early modern Europe, green was the color commonly associated with wealth, merchants, bankers, and the gentry, while red was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Rotunda
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ''ABCD'' would be denoted . Characterizations A convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals) * A convex quadrilateral wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |