|
Riemannian Metric And Lie-bracket In Computational Anatomy
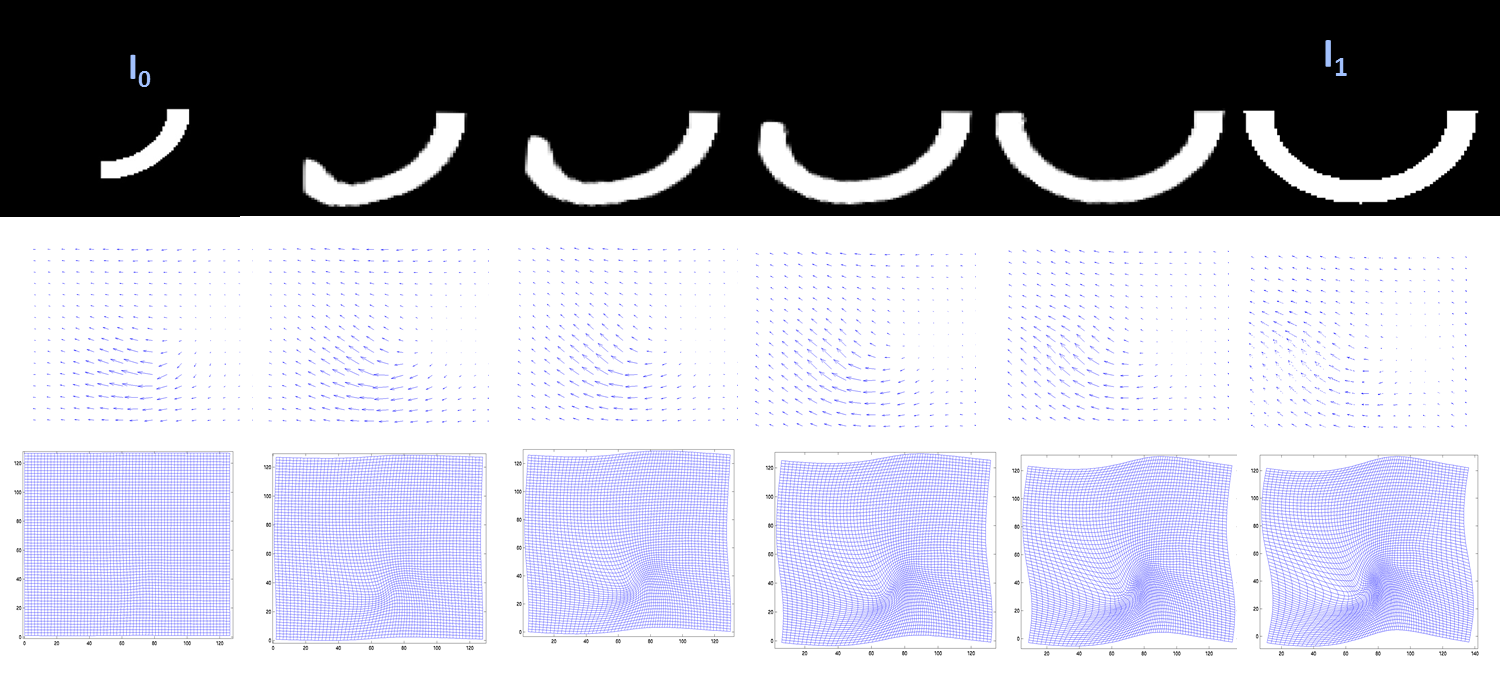
Computational anatomy (CA) is the study of shape and form in medical imaging. The study of deformable shapes in computational anatomy rely on high-dimensional diffeomorphism groups \varphi \in \operatorname_V which generate orbits of the form \mathcal \doteq \ . In CA, this orbit is in general considered a smooth Riemannian manifold since at every point of the manifold m \in \mathcal there is an inner product inducing the norm \, \cdot \, _m on the tangent space that varies smoothly from point to point in the manifold of shapes m \in \mathcal . This is generated by viewing the group of diffeomorphisms \varphi \in \operatorname_V as a Riemannian manifold with \, \cdot \, _\varphi , associated to the tangent space at \varphi \in\operatorname_V . This induces the norm and metric on the orbit m \in \mathcal under the action from the group of diffeomorphisms. The diffeomorphisms group generated as Lagrangian and Eulerian flows The diffeomorphisms in computat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Anatomy
Computational anatomy is an interdisciplinary field of biology focused on quantitative investigation and modelling of anatomical shapes variability. It involves the development and application of mathematical, statistical and data-analytical methods for modelling and simulation of biological structures. The field is broadly defined and includes foundations in anatomy, applied mathematics and pure mathematics, machine learning, computational mechanics, computational science, biological imaging, neuroscience, physics, probability, and statistics; it also has strong connections with fluid mechanics and geometric mechanics. Additionally, it complements newer, interdisciplinary fields like bioinformatics and neuroinformatics in the sense that its interpretation uses metadata derived from the original sensor imaging modalities (of which magnetic resonance imaging is one example). It focuses on the anatomical structures being imaged, rather than the medical imaging devices. It is simi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Review Letters
''Physical Review Letters'' (''PRL''), established in 1958, is a peer-reviewed, scientific journal that is published 52 times per year by the American Physical Society. As also confirmed by various measurement standards, which include the '' Journal Citation Reports'' impact factor and the journal ''h''-index proposed by Google Scholar, many physicists and other scientists consider ''Physical Review Letters'' to be one of the most prestigious journals in the field of physics. ''According to Google Scholar, PRL is the journal with the 9th journal h-index among all scientific journals'' ''PRL'' is published as a print journal, and is in electronic format, online and CD-ROM. Its focus is rapid dissemination of significant, or notable, results of fundamental research on all topics related to all fields of physics. This is accomplished by rapid publication of short reports, called "Letters". Papers are published and available electronically one article at a time. When published ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Mechanics
Fluid mechanics is the branch of physics concerned with the mechanics of fluids (liquids, gases, and plasmas) and the forces on them. It has applications in a wide range of disciplines, including mechanical, aerospace, civil, chemical and biomedical engineering, geophysics, oceanography, meteorology, astrophysics, and biology. It can be divided into fluid statics, the study of fluids at rest; and fluid dynamics, the study of the effect of forces on fluid motion. It is a branch of continuum mechanics, a subject which models matter without using the information that it is made out of atoms; that is, it models matter from a ''macroscopic'' viewpoint rather than from ''microscopic''. Fluid mechanics, especially fluid dynamics, is an active field of research, typically mathematically complex. Many problems are partly or wholly unsolved and are best addressed by numerical methods, typically using computers. A modern discipline, called computational fluid dynamics (CFD), i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invertible Matrix
In linear algebra, an -by- square matrix is called invertible (also nonsingular or nondegenerate), if there exists an -by- square matrix such that :\mathbf = \mathbf = \mathbf_n \ where denotes the -by- identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix is uniquely determined by , and is called the (multiplicative) ''inverse'' of , denoted by . Matrix inversion is the process of finding the matrix that satisfies the prior equation for a given invertible matrix . A square matrix that is ''not'' invertible is called singular or degenerate. A square matrix is singular if and only if its determinant is zero. Singular matrices are rare in the sense that if a square matrix's entries are randomly selected from any finite region on the number line or complex plane, the probability that the matrix is singular is 0, that is, it will "almost never" be singular. Non-square matrices (-by- matrices for which ) do not hav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LDDMM
Large deformation diffeomorphic metric mapping (LDDMM) is a specific suite of algorithms used for diffeomorphic mapping and manipulating dense imagery based on diffeomorphic metric mapping within the academic discipline of computational anatomy, to be distinguished from its precursor based on diffeomorphic mapping. The distinction between the two is that diffeomorphic metric maps satisfy the property that the length associated to their flow away from the identity induces a metric on the Computational anatomy#The Diffeomorphism Group of Computational Anatomy, group of diffeomorphisms, which in turn induces a metric on the orbit of Computational anatomy#Shapes and forms, shapes and forms within the field of Computational anatomy, Computational Anatomy. The study of shapes and forms with the metric of diffeomorphic metric mapping is called Computational Anatomy#Diffeomorphometry:the metric space of shapes and forms, diffeomorphometry. A diffeomorphic mapping system is a system design ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Advances In Mathematics
''Advances in Mathematics'' is a peer-reviewed scientific journal covering research on pure mathematics. It was established in 1961 by Gian-Carlo Rota. The journal publishes 18 issues each year, in three volumes. At the origin, the journal aimed at publishing articles addressed to a broader "mathematical community", and not only to mathematicians in the author's field. Herbert Busemann writes, in the preface of the first issue, "The need for expository articles addressing either all mathematicians or only those in somewhat related fields has long been felt, but little has been done outside of the USSR. The serial publication ''Advances in Mathematics'' was created in response to this demand." Abstracting and indexing The journal is abstracted and indexed in: * [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamilton's Principal Of Least Action
The stationary-action principle – also known as the principle of least action – is a variational principle that, when applied to the ''action'' of a mechanical system, yields the equations of motion for that system. The principle states that the trajectories (i.e. the solutions of the equations of motion) are '' stationary points'' of the system's ''action functional''. The term "least action" is a historical misnomer since the principle has no minimality requirement: the value of the action functional need not be minimal (even locally) on the trajectories. The principle can be used to derive Newtonian, Lagrangian and Hamiltonian equations of motion, and even general relativity (see Einstein–Hilbert action). In relativity, a different action must be minimized or maximized. The classical mechanics and electromagnetic expressions are a consequence of quantum mechanics. The stationary action method helped in the development of quantum mechanics. In 1933, the physicist Paul Di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medical Imaging
Medical imaging is the technique and process of imaging the interior of a body for clinical analysis and medical intervention, as well as visual representation of the function of some organs or tissues ( physiology). Medical imaging seeks to reveal internal structures hidden by the skin and bones, as well as to diagnose and treat disease. Medical imaging also establishes a database of normal anatomy and physiology to make it possible to identify abnormalities. Although imaging of removed organs and tissues can be performed for medical reasons, such procedures are usually considered part of pathology instead of medical imaging. Measurement and recording techniques that are not primarily designed to produce images, such as electroencephalography (EEG), magnetoencephalography (MEG), electrocardiography (ECG), and others, represent other technologies that produce data susceptible to representation as a parameter graph versus time or maps that contain data about the measurement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Bracket Of Vector Fields
In the mathematical field of differential topology, the Lie bracket of vector fields, also known as the Jacobi–Lie bracket or the commutator of vector fields, is an operator that assigns to any two vector fields ''X'' and ''Y'' on a smooth manifold ''M'' a third vector field denoted . Conceptually, the Lie bracket is the derivative of ''Y'' along the flow generated by ''X'', and is sometimes denoted ''\mathcal_X Y'' ("Lie derivative of Y along X"). This generalizes to the Lie derivative of any tensor field along the flow generated by ''X''. The Lie bracket is an R- bilinear operation and turns the set of all smooth vector fields on the manifold ''M'' into an (infinite-dimensional) Lie algebra. The Lie bracket plays an important role in differential geometry and differential topology, for instance in the Frobenius integrability theorem, and is also fundamental in the geometric theory of nonlinear control systems., nonholonomic systems; , feedback linearization. De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |