|
Regression Validation
In statistics, regression validation is the process of deciding whether the numerical results quantifying hypothesized relationships between variables, obtained from regression analysis, are acceptable as descriptions of the data. The validation process can involve analyzing the goodness of fit of the regression, analyzing whether the regression residuals are random, and checking whether the model's predictive performance deteriorates substantially when applied to data that were not used in model estimation. Goodness of fit One measure of goodness of fit is the coefficient of determination, often denoted, ''R''2. In ordinary least squares with an intercept, it ranges between 0 and 1. However, an ''R''2 close to 1 does not guarantee that the model fits the data well. For example, if the functional form of the model does not match the data, ''R''2 can be high despite a poor model fit. Anscombe's quartet consists of four example data sets with similarly high ''R''2 values, but ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
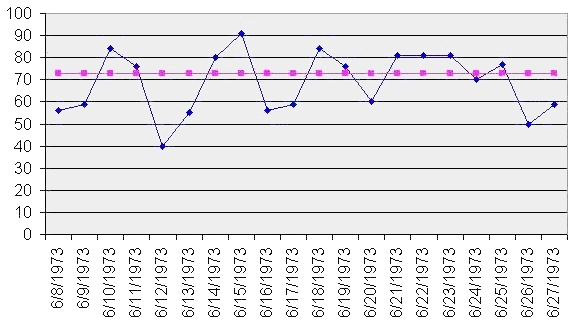
Run Chart
A run chart, also known as a run-sequence plot is a graph that displays observed data in a time sequence. Often, the data displayed represent some aspect of the output or performance of a manufacturing or other business process. It is therefore a form of line chart. Overview Run sequence plots are an easy way to graphically summarize a univariate data set. A common assumption of univariate data sets is that they behave like:NIST/SEMATECH (2003)"Run-Sequence Plot"In: ''e-Handbook of Statistical Methods'' 6/01/2003 (Date created). * random drawings; * from a fixed distribution; * with a common location; and * with a common scale. With run sequence plots, shifts in location and scale are typically quite evident. Also, outliers can easily be detected. Examples could include measurements of the fill level of bottles filled at a bottling plant or the water temperature of a dishwashing machine each time it is run. Time is generally represented on the horizontal (x) axis and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Squared Prediction Error
In statistics the mean squared prediction error (MSPE), also known as mean squared error of the predictions, of a smoothing, curve fitting, or regression (statistics), regression procedure is the expected value of the Square (algebra), squared prediction errors (PE), the squared deviation, square difference between the fitted values implied by the predictive function \widehat and the values of the (unobservable) true value ''g''. It is an inverse measure of the ''explanatory power'' of \widehat, and can be used in the process of cross-validation (statistics), cross-validation of an estimated model. Knowledge of ''g'' would be required in order to calculate the MSPE exactly; in practice, MSPE is estimated. Formulation If the smoothing or fitting procedure has projection matrix (i.e., hat matrix) ''L'', which maps the observed values vector y to predicted values vector \hat=Ly, then PE and MSPE are formulated as: :\operatorname=g(x_i)-\widehat(x_i), :\operatorname=\operatorname\left ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Squared Error
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the true value. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate. In machine learning, specifically empirical risk minimization, MSE may refer to the ''empirical'' risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution). The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the erro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
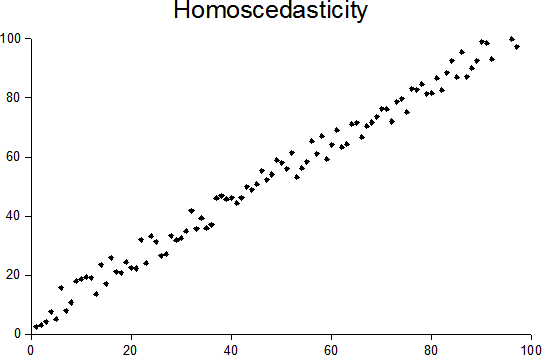
Heteroskedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as heterogeneity of variance. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. “Skedasticity” comes from the Ancient Greek word “skedánnymi”, meaning “to scatter”. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares est ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Durbin–Watson Statistic
In statistics, the Durbin–Watson statistic is a test statistic used to detect the presence of autocorrelation at lag 1 in the residuals (prediction errors) from a regression analysis. It is named after James Durbin and Geoffrey Watson. The small sample distribution of this ratio was derived by John von Neumann (von Neumann, 1941). Durbin and Watson (1950, 1951) applied this statistic to the residuals from least squares regressions, and developed bounds tests for the null hypothesis that the errors are serially uncorrelated against the alternative that they follow a first order autoregressive process. Note that the distribution of this test statistic does not depend on the estimated regression coefficients and the variance of the errors. A similar assessment can be also carried out with the Breusch–Godfrey test and the Ljung–Box test. Computing and interpreting the Durbin–Watson statistic If e_t is the residual given by e_t = \rho e_+ \nu_t , the Durbin-Watson test ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Serial Correlation
Autocorrelation, sometimes known as serial correlation in the discrete time case, measures the correlation of a signal with a delayed copy of itself. Essentially, it quantifies the similarity between observations of a random variable at different points in time. The analysis of autocorrelation is a mathematical tool for identifying repeating patterns or hidden periodicities within a signal obscured by noise. Autocorrelation is widely used in signal processing, time domain and time series analysis to understand the behavior of data over time. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Various time series models incorporate autocorrelation, such as unit root processes, trend-stationary processes, autoregressive processes, and moving average processes. Autocorrelation of stochastic processes In statistics, the autocorrelation of a real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Data
Binary data is data whose unit can take on only two possible states. These are often labelled as 0 and 1 in accordance with the binary numeral system and Boolean algebra. Binary data occurs in many different technical and scientific fields, where it can be called by different names including '' bit'' (binary digit) in computer science, '' truth value'' in mathematical logic and related domains and '' binary variable'' in statistics. Mathematical and combinatoric foundations A discrete variable that can take only one state contains zero information, and is the next natural number after 1. That is why the bit, a variable with only two possible values, is a standard primary unit of information. A collection of bits may have states: see binary number for details. Number of states of a collection of discrete variables depends exponentially on the number of variables, and only as a power law on number of states of each variable. Ten bits have more () states than three dec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Regression
In statistics, a logistic model (or logit model) is a statistical model that models the logit, log-odds of an event as a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) estimation theory, estimates the parameters of a logistic model (the coefficients in the linear or non linear combinations). In binary logistic regression there is a single binary variable, binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Designed Experiment
A design is the concept or proposal for an object, process, or system. The word ''design'' refers to something that is or has been intentionally created by a thinking agent, and is sometimes used to refer to the inherent nature of something – its design. The verb ''to design'' expresses the process of developing a design. In some cases, the direct construction of an object without an explicit prior plan may also be considered to be a design (such as in arts and crafts). A design is expected to have a purpose within a specific context, typically aiming to satisfy certain goals and constraints while taking into account aesthetic, functional and experiential considerations. Traditional examples of designs are architectural and engineering drawings, circuit diagrams, sewing patterns, and less tangible artefacts such as business process models.Dictionary meanings in the /dictionary.cambridge.org/dictionary/english/design Cambridge Dictionary of American English at /www.diction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Parameter
In statistics, as opposed to its general use in mathematics, a parameter is any quantity of a statistical population that summarizes or describes an aspect of the population, such as a mean or a standard deviation. If a population exactly follows a known and defined distribution, for example the normal distribution, then a small set of parameters can be measured which provide a comprehensive description of the population and can be considered to define a probability distribution for the purposes of extracting samples from this population. A "parameter" is to a population as a "statistic" is to a sample; that is to say, a parameter describes the true value calculated from the full population (such as the population mean), whereas a statistic is an estimated measurement of the parameter based on a sample (such as the sample mean, which is the mean of gathered data per sampling, called sample). Thus a "statistical parameter" can be more specifically referred to as a population ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |