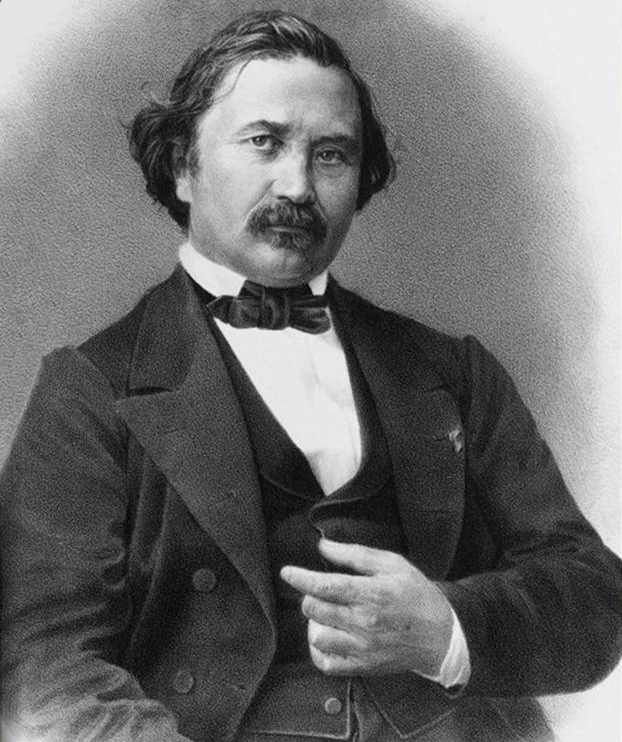|
Ramanujan Prime
In mathematics, a Ramanujan prime is a prime number that satisfies a result proven by Srinivasa Ramanujan relating to the prime-counting function. Origins and definition In 1919, Ramanujan published a new proof of Bertrand's postulate which, as he notes, was first proved by Chebyshev. At the end of the two-page published paper, Ramanujan derived a generalized result, and that is: : \pi(x) - \pi\left( \frac x 2 \right) \ge 1,2,3,4,5,\ldots \text x \ge 2, 11, 17, 29, 41, \ldots \text where \pi(x) is the prime-counting function, equal to the number of primes less than or equal to ''x''. The converse of this result is the definition of Ramanujan primes: :The ''n''th Ramanujan prime is the least integer ''Rn'' for which \pi(x) - \pi(x/2) \ge n, for all ''x'' ≥ ''Rn''. In other words: Ramanujan primes are the least integers ''Rn'' for which there are at least ''n'' primes between ''x'' and ''x''/2 for all ''x'' ≥ ''Rn''. The first five Ramanujan pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorization, factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow primality test, method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Srinivasa Ramanujan
Srinivasa Ramanujan Aiyangar (22 December 188726 April 1920) was an Indian mathematician. Often regarded as one of the greatest mathematicians of all time, though he had almost no formal training in pure mathematics, he made substantial contributions to mathematical analysis, number theory, infinite series, and continued fractions, including solutions to mathematical problems then considered unsolvable. Ramanujan initially developed his own mathematical research in isolation. According to Hans Eysenck, "he tried to interest the leading professional mathematicians in his work, but failed for the most part. What he had to show them was too novel, too unfamiliar, and additionally presented in unusual ways; they could not be bothered". Seeking mathematicians who could better understand his work, in 1913 he began a mail correspondence with the English mathematician G. H. Hardy at the University of Cambridge, England. Recognising Ramanujan's work as extraordinary, Hardy arranged ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime-counting Function
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number . It is denoted by (unrelated to the number ). A symmetric variant seen sometimes is , which is equal to if is exactly a prime number, and equal to otherwise. That is, the number of prime numbers less than , plus half if equals a prime. Growth rate Of great interest in number theory is the growth rate of the prime-counting function. It was conjectured in the end of the 18th century by Gauss and by Legendre to be approximately \frac where is the natural logarithm, in the sense that \lim_ \frac=1. This statement is the prime number theorem. An equivalent statement is \lim_\frac=1 where is the logarithmic integral function. The prime number theorem was first proved in 1896 by Jacques Hadamard and by Charles de la Vallée Poussin independently, using properties of the Riemann zeta function introduced by Riemann in 1859. Proof ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bertrand's Postulate
In number theory, Bertrand's postulate is the theorem that for any integer n > 3, there exists at least one prime number p with :n < p < 2n - 2. A less restrictive formulation is: for every , there is always at least one prime such that : Another formulation, where is the -th prime, is: for : This statement was first conjectured in 1845 by Joseph Bertrand (1822–1900). Bertrand himself verified his statement for all integers . His conjecture was completely Proof of Bertrand's postulate, proved by Pafnuty Chebyshev, Chebyshev (1821–1894) in 1852 and so the postulate is also called the Bertrand–Chebyshev theorem or Chebyshev's theorem. Chebyshev's theorem can also be stated as a relationship with , the prime-counting function (number of primes less than or equal to ): ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev ( rus, Пафну́тий Льво́вич Чебышёв, p=pɐfˈnutʲɪj ˈlʲvovʲɪtɕ tɕɪbɨˈʂof) ( – ) was a Russian mathematician and considered to be the founding father of Russian mathematics. Chebyshev is known for his fundamental contributions to the fields of probability, statistics, mechanics, and number theory. A number of important mathematical concepts are named after him, including the Chebyshev inequality (which can be used to prove the weak law of large numbers), the Bertrand–Chebyshev theorem, Chebyshev polynomials, Chebyshev linkage, and Chebyshev bias. Transcription The surname Chebyshev has been transliterated in several different ways, like Tchebichef, Tchebychev, Tchebycheff, Tschebyschev, Tschebyschef, Tschebyscheff, Čebyčev, Čebyšev, Chebysheff, Chebychov, Chebyshov (according to native Russian speakers, this one provides the closest pronunciation in English to the correct pronunciation in old Russian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic Analysis
In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing Limit (mathematics), limiting behavior. As an illustration, suppose that we are interested in the properties of a function as becomes very large. If , then as becomes very large, the term becomes insignificant compared to . The function is said to be "''asymptotically equivalent'' to , as ". This is often written symbolically as , which is read as " is asymptotic to ". An example of an important asymptotic result is the prime number theorem. Let denote the prime-counting function (which is not directly related to the constant pi), i.e. is the number of prime numbers that are less than or equal to . Then the theorem states that \pi(x)\sim\frac. Asymptotic analysis is commonly used in computer science as part of the analysis of algorithms and is often expressed there in terms of big O notation. Definition Formally, given functions and , we define a binary relation f( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Journal Of Number Theory
International is an adjective (also used as a noun) meaning "between nations". International may also refer to: Music Albums * ''International'' (Kevin Michael album), 2011 * ''International'' (New Order album), 2002 * ''International'' (The Three Degrees album), 1975 *''International'', 2018 album by L'Algérino Songs * The Internationale, the left-wing anthem * "International" (Chase & Status song), 2014 * "International", by Adventures in Stereo from ''Monomania'', 2000 * "International", by Brass Construction from ''Renegades'', 1984 * "International", by Thomas Leer from ''The Scale of Ten'', 1985 * "International", by Kevin Michael from ''International'' (Kevin Michael album), 2011 * "International", by McGuinness Flint from ''McGuinness Flint'', 1970 * "International", by Orchestral Manoeuvres in the Dark from '' Dazzle Ships'', 1983 * "International (Serious)", by Estelle from '' All of Me'', 2012 Politics * Internationalism (politics) * Political international, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |