|
Radial Basis Function Network
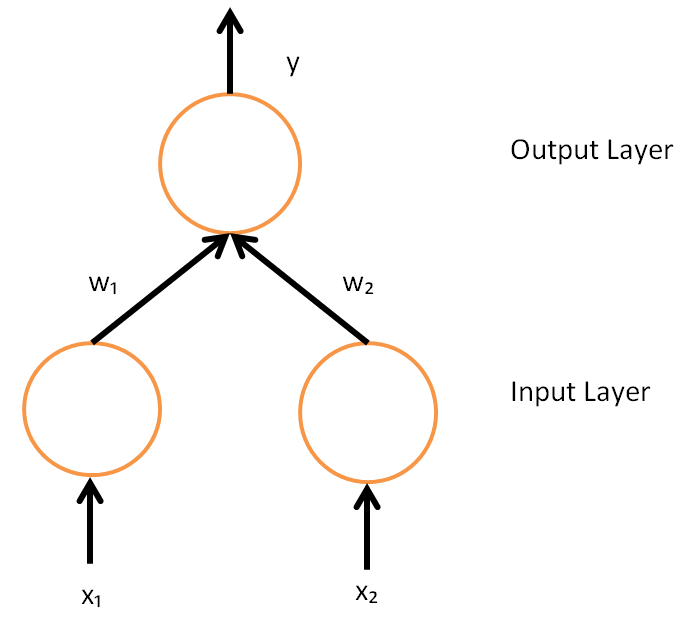
In the field of mathematical modeling, a radial basis function network is an artificial neural network that uses radial basis functions as activation functions. The output of the network is a linear combination of radial basis functions of the inputs and neuron parameters. Radial basis function networks have many uses, including function approximation, time series prediction, classification, and system control. They were first formulated in a 1988 paper by Broomhead and Lowe, both researchers at the Royal Signals and Radar Establishment. Network architecture Radial basis function (RBF) networks typically have three layers: an input layer, a hidden layer with a non-linear RBF activation function and a linear output layer. The input can be modeled as a vector of real numbers \mathbf \in \mathbb^n. The output of the network is then a scalar function of the input vector, \varphi : \mathbb^n \to \mathbb , and is given by :\varphi(\mathbf) = \sum_^N a_i \rho(, , \mathbf-\mathbf_i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Modeling
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical modeling''. Mathematical models are used in applied mathematics and in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). It can also be taught as a subject in its own right. The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Method
In numerical analysis, the Newton–Raphson method, also known simply as Newton's method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valued function. The most basic version starts with a real-valued function , its derivative , and an initial guess for a root of . If satisfies certain assumptions and the initial guess is close, then x_ = x_0 - \frac is a better approximation of the root than . Geometrically, is the x-intercept of the tangent of the graph of at : that is, the improved guess, , is the unique root of the linear approximation of at the initial guess, . The process is repeated as x_ = x_n - \frac until a sufficiently precise value is reached. The number of correct digits roughly doubles with each step. This algorithm is first in the class of Householder's methods, and was succeeded by Halley's method. The method can also be extended t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Descent
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a trajectory that maximizes that function; the procedure is then known as ''gradient ascent''. It is particularly useful in machine learning for minimizing the cost or loss function. Gradient descent should not be confused with local search algorithms, although both are iterative methods for optimization. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudoinverse
In mathematics, and in particular, algebra, a generalized inverse (or, g-inverse) of an element ''x'' is an element ''y'' that has some properties of an inverse element but not necessarily all of them. The purpose of constructing a generalized inverse of a matrix is to obtain a matrix that can serve as an inverse in some sense for a wider class of matrices than invertible matrices. Generalized inverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup. This article describes generalized inverses of a matrix A. A matrix A^\mathrm \in \mathbb^ is a generalized inverse of a matrix A \in \mathbb^ if AA^\mathrmA = A. A generalized inverse exists for an arbitrary matrix, and when a matrix has a regular inverse, this inverse is its unique generalized inverse. Motivation Consider the linear system :Ax = y where A is an m \times n matrix and y \in \mathcal C(A), the column space of A. If m = n and A is nonsingular then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Clustering
Cluster analysis or clustering is the data analyzing technique in which task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some specific sense defined by the analyst) to each other than to those in other groups (clusters). It is a main task of exploratory data analysis, and a common technique for statistical data analysis, used in many fields, including pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Cluster analysis refers to a family of algorithms and tasks rather than one specific algorithm. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with small distances between cluster members, dense areas of the data space, intervals or particular statistical distributions. Clustering ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backpropagation
In machine learning, backpropagation is a gradient computation method commonly used for training a neural network to compute its parameter updates. It is an efficient application of the chain rule to neural networks. Backpropagation computes the gradient of a loss function with respect to the weights of the network for a single input–output example, and does so efficiently, computing the gradient one layer at a time, iterating backward from the last layer to avoid redundant calculations of intermediate terms in the chain rule; this can be derived through dynamic programming. Strictly speaking, the term ''backpropagation'' refers only to an algorithm for efficiently computing the gradient, not how the gradient is used; but the term is often used loosely to refer to the entire learning algorithm – including how the gradient is used, such as by stochastic gradient descent, or as an intermediate step in a more complicated optimizer, such as Adaptive Moment Estimation. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (machine Learning)
In mathematics, statistics, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the answer to a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, the following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularization is essentially ubiquitous in modern machine learnin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
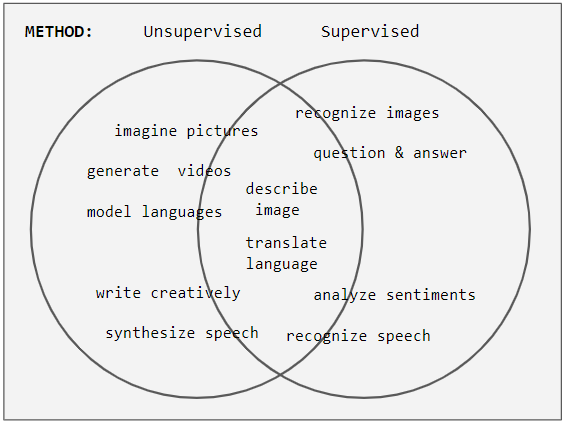
Unsupervised Learning
Unsupervised learning is a framework in machine learning where, in contrast to supervised learning, algorithms learn patterns exclusively from unlabeled data. Other frameworks in the spectrum of supervisions include weak- or semi-supervision, where a small portion of the data is tagged, and self-supervision. Some researchers consider self-supervised learning a form of unsupervised learning. Conceptually, unsupervised learning divides into the aspects of data, training, algorithm, and downstream applications. Typically, the dataset is harvested cheaply "in the wild", such as massive text corpus obtained by web crawling, with only minor filtering (such as Common Crawl). This compares favorably to supervised learning, where the dataset (such as the ImageNet1000) is typically constructed manually, which is much more expensive. There were algorithms designed specifically for unsupervised learning, such as clustering algorithms like k-means, dimensionality reduction techniques l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-means Clustering
''k''-means clustering is a method of vector quantization, originally from signal processing, that aims to partition of a set, partition ''n'' observations into ''k'' clusters in which each observation belongs to the cluster (statistics), cluster with the nearest mean (cluster centers or cluster centroid), serving as a prototype of the cluster. This results in a partitioning of the data space into Voronoi cells. ''k''-means clustering minimizes within-cluster variances (squared Euclidean distances), but not regular Euclidean distances, which would be the more difficult Weber problem: the mean optimizes squared errors, whereas only the geometric median minimizes Euclidean distances. For instance, better Euclidean solutions can be found using k-medians clustering, ''k''-medians and k-medoids, ''k''-medoids. The problem is computationally difficult (NP-hardness, NP-hard); however, efficient heuristic algorithms converge quickly to a local optimum. These are usually similar to the ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kronecker Delta Function
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise: \delta_ = \begin 0 &\text i \neq j, \\ 1 &\text i=j. \end or with use of Iverson brackets: \delta_ = =j, For example, \delta_ = 0 because 1 \ne 2, whereas \delta_ = 1 because 3 = 3. The Kronecker delta appears naturally in many areas of mathematics, physics, engineering and computer science, as a means of compactly expressing its definition above. Generalized versions of the Kronecker delta have found applications in differential geometry and modern tensor calculus, particularly in formulations of gauge theory and topological field models. In linear algebra, the n\times n identity matrix \mathbf has entries equal to the Kronecker delta: I_ = \delta_ where i and j take the values 1,2,\cdots,n, and the inner product of vectors can be written as \mathbf\cdot\mathbf = \sum_^n a_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Linearity
In mathematics, a differentiable function of one Real number, real variable is a Function (mathematics), function whose derivative exists at each point in its Domain of a function, domain. In other words, the Graph of a function, graph of a differentiable function has a non-Vertical tangent, vertical tangent line at each interior point in its domain. A differentiable function is Smoothness, smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or Cusp (singularity), cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |