|
Quantum Image Processing
Quantum image processing (QIMP) is using quantum computing or quantum information processing to create and work with quantum images. Due to some of the properties inherent to quantum computation, notably entanglement and parallelism, it is hoped that QIMP technologies will offer capabilities and performances that surpass their traditional equivalents, in terms of computing speed, security, and minimum storage requirements. Background A. Y. Vlasov's work in 1997 focused on the use of a quantum system to recognize orthogonal images. This was followed by efforts using quantum algorithms to search specific patterns in binary images and detect the posture of certain targets. Notably, more optics-based interpretation for quantum imaging were initially experimentally demonstrated in and formalized in after seven years. In 2003, Salvador Venegas-Andraca and S. Bose presented Qubit Lattice, the first published general model for storing, processing and retrieving images using quantum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Computing
Quantum computing is a type of computation whose operations can harness the phenomena of quantum mechanics, such as superposition, interference, and entanglement. Devices that perform quantum computations are known as quantum computers. Though current quantum computers may be too small to outperform usual (classical) computers for practical applications, larger realizations are believed to be capable of solving certain computational problems, such as integer factorization (which underlies RSA encryption), substantially faster than classical computers. The study of quantum computing is a subfield of quantum information science. There are several models of quantum computation with the most widely used being quantum circuits. Other models include the quantum Turing machine, quantum annealing, and adiabatic quantum computation. Most models are based on the quantum bit, or "qubit", which is somewhat analogous to the bit in classical computation. A qubit can be in a 1 or 0 quantu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Watermark
A watermark is an identifying image or pattern in paper that appears as various shades of lightness/darkness when viewed by transmitted light (or when viewed by reflected light, atop a dark background), caused by thickness or density variations in the paper. Watermarks have been used on postage stamps, currency, and other government documents to discourage counterfeiting. There are two main ways of producing watermarks in paper; the ''dandy roll process'', and the more complex ''cylinder mould process''. Watermarks vary greatly in their visibility; while some are obvious on casual inspection, others require some study to pick out. Various aids have been developed, such as ''watermark fluid'' that wets the paper without damaging it. A watermark is very useful in the examination of paper because it can be used for dating documents and artworks, identifying sizes, mill trademarks and locations, and determining the quality of a sheet of paper. The word is also used for digital ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
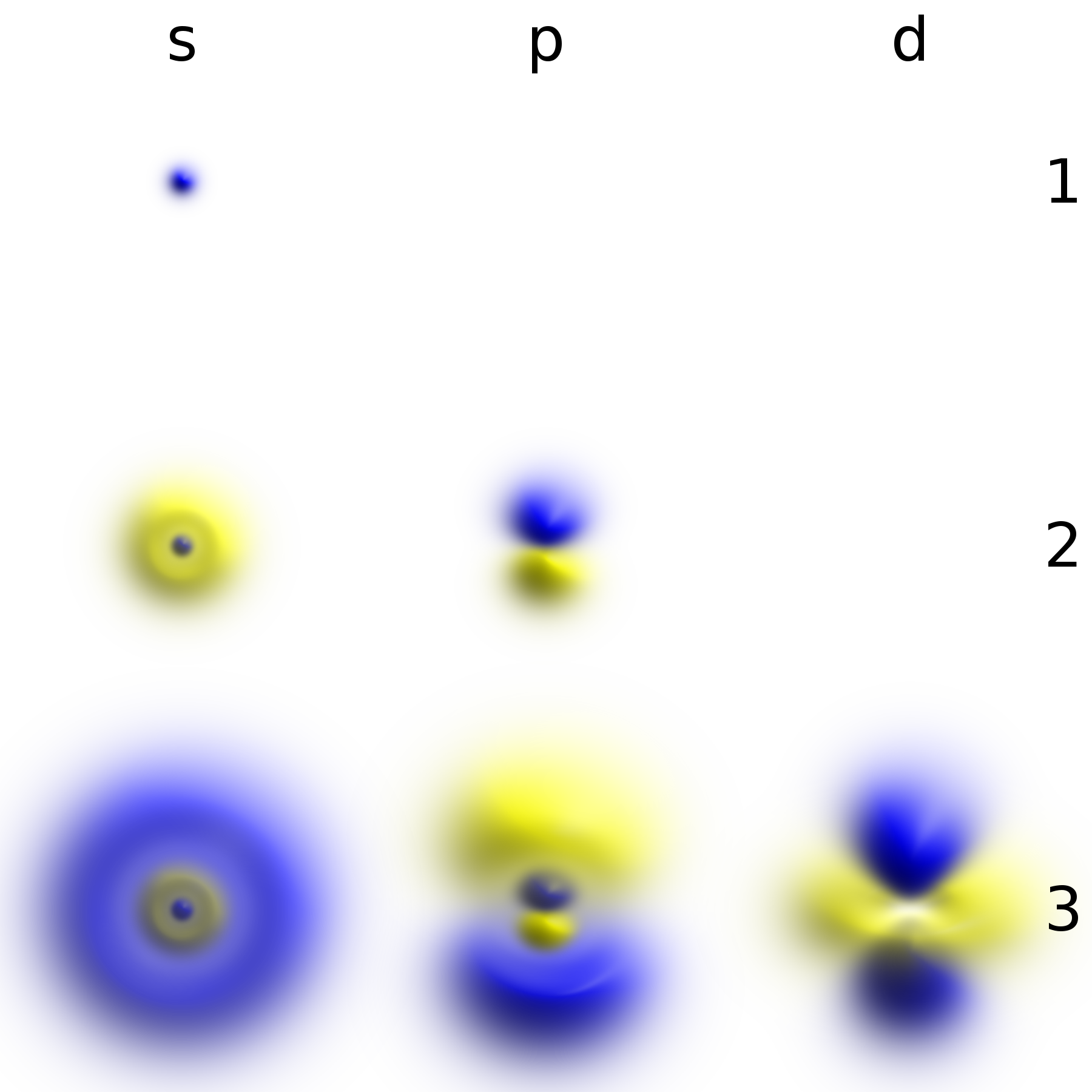
Quantum Image
Quantum computation, which exploits quantum parallelism, is in principle faster than a classical computer for certain problems. Quantum image is encoding the image information in quantum-mechanical systems instead of classical ones and replacing classical with quantum information processing may alleviate some of these challenges. Humans obtain most of their information through their eyes. Accordingly, the analysis of visual data is one of the most important functions of our brain and it has evolved high efficiency in processing visual data. Currently, visual information like images and videos constitutes the largest part of data traffic in the internet. Processing of this information requires ever-larger computational power. The laws of quantum mechanics allow one to reduce the required resources for some tasks by many orders of magnitude if the image data are encoded in the quantum state of a suitable physical system. The researchers discuss a suitable method for encoding image dat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Computing
Quantum computing is a type of computation whose operations can harness the phenomena of quantum mechanics, such as superposition, interference, and entanglement. Devices that perform quantum computations are known as quantum computers. Though current quantum computers may be too small to outperform usual (classical) computers for practical applications, larger realizations are believed to be capable of solving certain computational problems, such as integer factorization (which underlies RSA encryption), substantially faster than classical computers. The study of quantum computing is a subfield of quantum information science. There are several models of quantum computation with the most widely used being quantum circuits. Other models include the quantum Turing machine, quantum annealing, and adiabatic quantum computation. Most models are based on the quantum bit, or "qubit", which is somewhat analogous to the bit in classical computation. A qubit can be in a 1 or 0 quantu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unitary Operator
In functional analysis, a unitary operator is a surjective bounded operator on a Hilbert space that preserves the inner product. Unitary operators are usually taken as operating ''on'' a Hilbert space, but the same notion serves to define the concept of isomorphism ''between'' Hilbert spaces. A unitary element is a generalization of a unitary operator. In a unital algebra, an element of the algebra is called a unitary element if , where is the identity element. Definition Definition 1. A ''unitary operator'' is a bounded linear operator on a Hilbert space that satisfies , where is the adjoint of , and is the identity operator. The weaker condition defines an '' isometry''. The other condition, , defines a ''coisometry''. Thus a unitary operator is a bounded linear operator which is both an isometry and a coisometry, or, equivalently, a surjective isometry. An equivalent definition is the following: Definition 2. A ''unitary operator'' is a bounded linear operato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Haar Wavelet
In mathematics, the Haar wavelet is a sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal basis. The Haar sequence is now recognised as the first known wavelet basis and extensively used as a teaching example. The Haar sequence was proposed in 1909 by Alfréd Haar. Haar used these functions to give an example of an orthonormal system for the space of square-integrable functions on the unit interval , 1 The study of wavelets, and even the term "wavelet", did not come until much later. As a special case of the Daubechies wavelet, the Haar wavelet is also known as Db1. The Haar wavelet is also the simplest possible wavelet. The technical disadvantage of the Haar wavelet is that it is not continuous, and therefore not differentiable. This property can, however, be an advantage for t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hadamard Transform
The Hadamard transform (also known as the Walsh–Hadamard transform, Hadamard–Rademacher–Walsh transform, Walsh transform, or Walsh–Fourier transform) is an example of a generalized class of Fourier transforms. It performs an orthogonal, symmetric, involutive, linear operation on real numbers (or complex, or hypercomplex numbers, although the Hadamard matrices themselves are purely real). The Hadamard transform can be regarded as being built out of size-2 discrete Fourier transforms (DFTs), and is in fact equivalent to a multidimensional DFT of size . It decomposes an arbitrary input vector into a superposition of Walsh functions. The transform is named for the French mathematician Jacques Hadamard (), the German-American mathematician Hans Rademacher, and the American mathematician Joseph L. Walsh. Definition The Hadamard transform ''H''''m'' is a 2''m'' × 2''m'' matrix, the Hadamard matrix (scaled by a normalization factor), that transforms 2''m'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear
Linearity is the property of a mathematical relationship ('' function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear relationship of voltage and current in an electrical conductor ( Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships are ''nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. The word linear comes from Latin ''linearis'', "pertaining to or resembling a line". In mathematics In mathematics, a linear map or linear function ''f''(''x'') is a function that satisfies the two properties: * Additivity: . * Homogeneity of degree 1: for all α. These properties are known as the superposition principle. In this definition, ''x'' is not necessarily ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pixel
In digital imaging, a pixel (abbreviated px), pel, or picture element is the smallest addressable element in a raster image, or the smallest point in an all points addressable display device. In most digital display devices, pixels are the smallest element that can be manipulated through software. Each pixel is a sample of an original image; more samples typically provide more accurate representations of the original. The intensity of each pixel is variable. In color imaging systems, a color is typically represented by three or four component intensities such as red, green, and blue, or cyan, magenta, yellow, and black. In some contexts (such as descriptions of camera sensors), ''pixel'' refers to a single scalar element of a multi-component representation (called a ''photosite'' in the camera sensor context, although '' sensel'' is sometimes used), while in yet other contexts (like MRI) it may refer to a set of component intensities for a spatial position. Etymology ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum State
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in time exhausts all that can be predicted about the system's behavior. A mixture of quantum states is again a quantum state. Quantum states that cannot be written as a mixture of other states are called pure quantum states, while all other states are called mixed quantum states. A pure quantum state can be represented by a ray in a Hilbert space over the complex numbers, while mixed states are represented by density matrices, which are positive semidefinite operators that act on Hilbert spaces. Pure states are also known as state vectors or wave functions, the latter term applying particularly when they are represented as functions of position or momentum. For example, when dealing with the energy spectrum of the electron in a hydrogen a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)