|
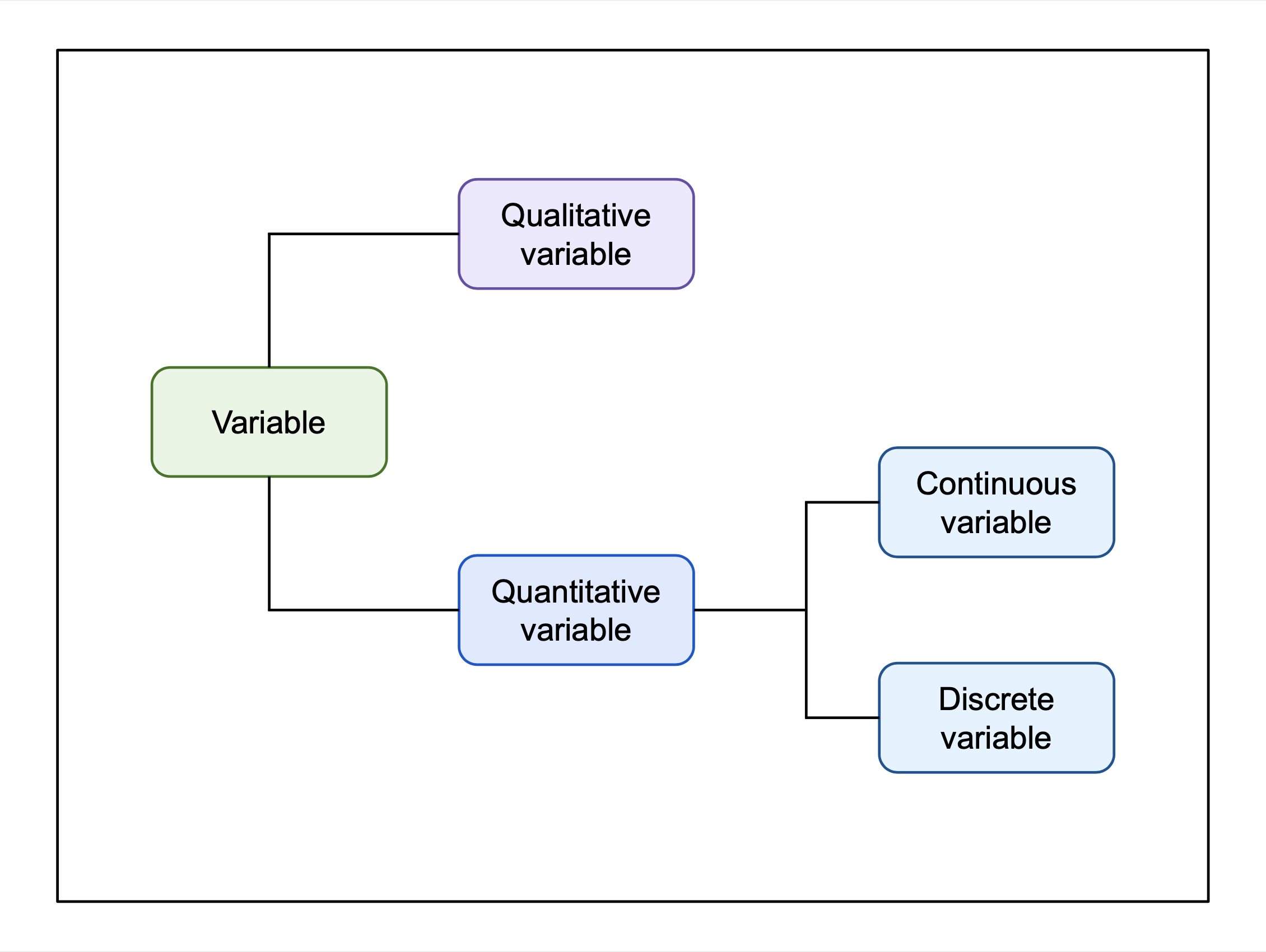
Quantitative Variable
In mathematics and statistics, a quantitative variable may be continuous or discrete. If it can take on two real values and all the values between them, the variable is continuous in that interval. If it can take on a value such that there is a non-infinitesimal gap on each side of it containing no values that the variable can take on, then it is discrete around that value. In some contexts, a variable can be discrete in some ranges of the number line and continuous in others. In statistics, continuous and discrete variables are distinct statistical data types which are described with different probability distributions. Continuous variable A continuous variable is a variable such that there are possible values between any two values. For example, a variable over a non-empty range of the real numbers is continuous if it can take on any value in that range. Methods of calculus are often used in problems in which the variables are continuous, for example in continuous optimi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Or Discrete Variables Example
Continuity or continuous may refer to: Mathematics * Continuity (mathematics), the opposing concept to discreteness; common examples include ** Continuous probability distribution or random variable in probability and statistics ** Continuous game, a generalization of games used in game theory ** Law of continuity, a heuristic principle of Gottfried Leibniz * Continuous function, in particular: ** Continuity (topology), a generalization to functions between topological spaces ** Scott continuity, for functions between posets ** Continuity (set theory), for functions between ordinals ** Continuity (category theory), for functors ** Graph continuity, for payoff functions in game theory * Continuity theorem may refer to one of two results: ** Lévy's continuity theorem, on random variables ** Kolmogorov continuity theorem, on stochastic processes * In geometry: ** Parametric continuity, for parametrised curves ** Geometric continuity, a concept primarily applied to the conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Regression
In statistics, a logistic model (or logit model) is a statistical model that models the logit, log-odds of an event as a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) estimation theory, estimates the parameters of a logistic model (the coefficients in the linear or non linear combinations). In binary logistic regression there is a single binary variable, binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent Variable
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, on the other hand, are not seen as depending on any other variable in the scope of the experiment in question. Rather, they are controlled by the experimenter. In pure mathematics In mathematics, a function is a rule for taking an input (in the simplest case, a number or set of numbers)Carlson, Robert. A concrete introduction to real analysis. CRC Press, 2006. p.183 and providing an output (which may also be a number). A symbol that stands for an arbitrary input is called an independent variable, while a symbol that stands for an arbitrary output is called a dependent variable. The most common symbol for the input is , and the most common symbol for the output is ; the functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dummy Variable (statistics)
In regression analysis, a dummy variable (also known as indicator variable or just dummy) is one that takes a binary value (0 or 1) to indicate the absence or presence of some categorical effect that may be expected to shift the outcome. For example, if we were studying the relationship between biological sex and income, we could use a dummy variable to represent the sex of each individual in the study. The variable could take on a value of 1 for males and 0 for females (or vice versa). In machine learning this is known as one-hot encoding. Dummy variables are commonly used in regression analysis to represent categorical variables that have more than two levels, such as education level or occupation. In this case, multiple dummy variables would be created to represent each level of the variable, and only one dummy variable would take on a value of 1 for each observation. Dummy variables are useful because they allow us to include categorical variables in our analysis, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical
Empirical evidence is evidence obtained through sense experience or experimental procedure. It is of central importance to the sciences and plays a role in various other fields, like epistemology and law. There is no general agreement on how the terms ''evidence'' and ''empirical'' are to be defined. Often different fields work with quite different conceptions. In epistemology, evidence is what justifies beliefs or what determines whether holding a certain belief is rational. This is only possible if the evidence is possessed by the person, which has prompted various epistemologists to conceive evidence as private mental states like experiences or other beliefs. In philosophy of science, on the other hand, evidence is understood as that which '' confirms'' or ''disconfirms'' scientific hypotheses and arbitrates between competing theories. For this role, evidence must be public and uncontroversial, like observable physical objects or events and unlike private mental states, so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
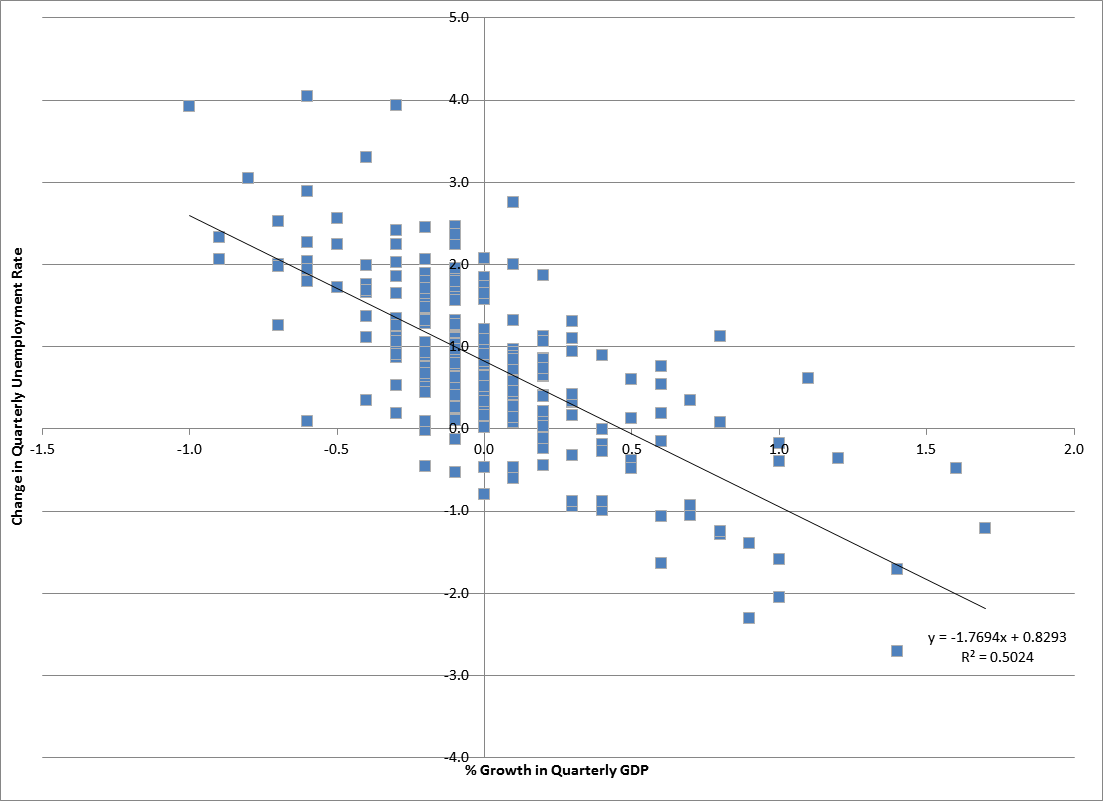
Econometrics
Econometrics is an application of statistical methods to economic data in order to give empirical content to economic relationships. M. Hashem Pesaran (1987). "Econometrics", '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8–22 Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1 p. 1–34Abstract ( 2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference." An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships." Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today. A basic tool for econometrics is the multiple linear regression model. ''Econome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difference Equation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Time
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled. Discrete time Discrete time views values of variables as occurring at distinct, separate "points in time", or equivalently as being unchanged throughout each non-zero region of time ("time period")—that is, time is viewed as a discrete variable. Thus a non-time variable jumps from one value to another as time moves from one time period to the next. This view of time corresponds to a digital clock that gives a fixed reading of 10:37 for a while, and then jumps to a new fixed reading of 10:38, etc. In this framework, each variable of interest is measured once at each time period. The number of measurements between any two time periods is finite. Measurements are typically made at sequential integer values of the variable "time". A discrete signal or discrete-time signal is a time series consisting of a sequence of quantities. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Mass Function
In probability and statistics, a probability mass function (sometimes called ''probability function'' or ''frequency function'') is a function that gives the probability that a discrete random variable is exactly equal to some value. Sometimes it is also known as the discrete probability density function. The probability mass function is often the primary means of defining a discrete probability distribution, and such functions exist for either scalar or multivariate random variables whose domain is discrete. A probability mass function differs from a continuous probability density function (PDF) in that the latter is associated with continuous rather than discrete random variables. A continuous PDF must be integrated over an interval to yield a probability. The value of the random variable having the largest probability mass is called the mode. Formal definition Probability mass function is the probability distribution of a discrete random variable, and provides the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints (other than the integer constraints) are linear. Integer programming is NP-complete. In particular, the special case of 0–1 integer linear programming, in which unknowns are binary, and only the restrictions must be satisfied, is one of Karp's 21 NP-complete problems. If some decision variables are not discrete, the problem is known as a mixed-integer programming problem. Canonical and standard form for ILPs In integer linear programming, the ''canonical form'' is distinct from the ''standard form''. An integer linear program in canonical form is expressed thus (note that it is the \mathbf vector which is to be decided): : \begin & \underset && \mathbf^\mathrm \mathbf\\ & \text && A \mathbf \le \mathbf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |