|
Pulse Duration
In signal processing and telecommunications, pulse duration is the interval between the time, during the first transition, that the amplitude of the pulse reaches a specified fraction (level) of its final amplitude, and the time the pulse amplitude drops, on the last transition, to the same level. The interval between the 50% points of the final amplitude is usually used to determine or define pulse duration, and this is understood to be the case unless otherwise specified. Other fractions of the final amplitude, e.g., 90% or 1/ e, may also be used, as may the root mean square (rms) value of the pulse amplitude. In radar Radar is a system that uses radio waves to determine the distance ('' ranging''), direction ( azimuth and elevation angles), and radial velocity of objects relative to the site. It is a radiodetermination method used to detect and track ..., the pulse duration is the time the radar's transmitter is energized during each cycle. References * * {{Auth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pulse Duration Example Picture 50perc
In medicine, the pulse refers to the rhythmic pulsations (expansion and contraction) of an artery in response to the cardiac cycle (heartbeat). The pulse may be felt (palpated) in any place that allows an artery to be compressed near the surface of the body close to the skin, such as at the neck (carotid artery), wrist (radial artery or ulnar artery), at the groin (femoral artery), behind the knee (popliteal artery), near the ankle joint (posterior tibial artery), and on foot (dorsalis pedis artery). The pulse is most commonly measured at the wrist or neck for adults and at the brachial artery (inner upper arm between the shoulder and elbow) for infants and very young children. A sphygmograph is an instrument for measuring the pulse. Physiology Claudius Galen was perhaps the first physiologist to describe the pulse. The pulse is an expedient tactile method of determination of systolic blood pressure to a trained observer. Diastolic blood pressure is non-palpable and unobse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
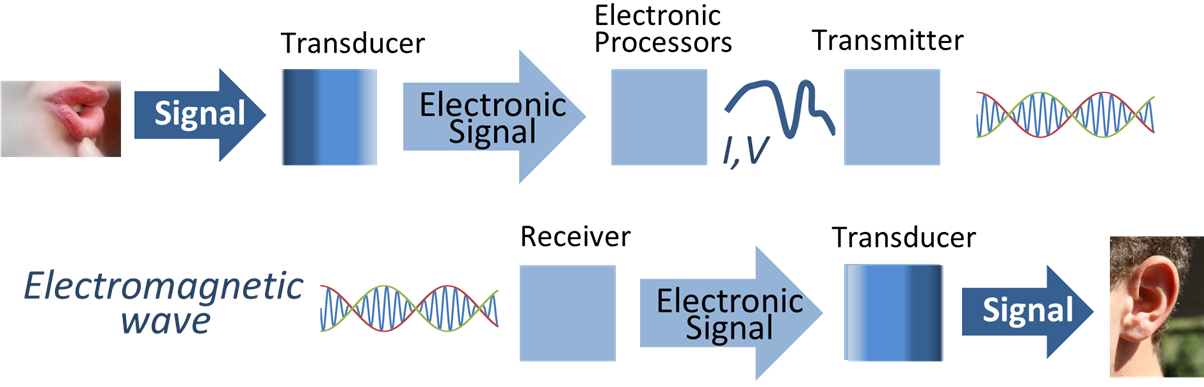
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Telecommunications
Telecommunication, often used in its plural form or abbreviated as telecom, is the transmission of information over a distance using electronic means, typically through cables, radio waves, or other communication technologies. These means of transmission may be divided into communication channels for multiplexing, allowing for a single medium to transmit several concurrent Session (computer science), communication sessions. Long-distance technologies invented during the 20th and 21st centuries generally use electric power, and include the electrical telegraph, telegraph, telephone, television, and radio. Early telecommunication networks used metal wires as the medium for transmitting signals. These networks were used for telegraphy and telephony for many decades. In the first decade of the 20th century, a revolution in wireless communication began with breakthroughs including those made in radio communications by Guglielmo Marconi, who won the 1909 Nobel Prize in Physics. Othe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequence events, to compare the duration of events (or the intervals between them), and to quantify rates of change of quantities in material reality or in the qualia, conscious experience. Time is often referred to as a fourth dimension, along with Three-dimensional space, three spatial dimensions. Time is one of the seven fundamental physical quantities in both the International System of Units (SI) and International System of Quantities. The SI base unit of time is the second, which is defined by measuring the electronic transition frequency of caesium atoms. General relativity is the primary framework for understanding how spacetime works. Through advances in both theoretical and experimental investigations of spacetime, it has been shown ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pulse Amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplitude (see below), which are all functions of the magnitude of the differences between the variable's extreme values. In older texts, the phase of a periodic function is sometimes called the amplitude. Definitions Peak amplitude and semi-amplitude For symmetric periodic waves, like sine waves or triangle waves, ''peak amplitude'' and ''semi amplitude'' are the same. Peak amplitude In audio system measurements, telecommunications and others where the measurand is a signal that swings above and below a reference value but is not sinusoidal, peak amplitude is often used. If the reference is zero, this is the maximum absolute value of the signal; if the reference is a mean value (DC component), the peak amplitude is the maximum absolute val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pulse (signal Processing)
A pulse in signal processing is a rapid, transient change in the amplitude of a signal from a baseline value to a higher or lower value, followed by a rapid return to the baseline value. Pulse shapes Pulse shapes can arise out of a process called pulse shaping. Optimum pulse shape depends on the application. Rectangular pulse These can be found in pulse waves, square waves, boxcar functions, and rectangular functions. In digital signals the up and down transitions between high and low levels are called the rising edge and the falling edge. In digital systems the detection of these sides or action taken in response is termed edge-triggered, rising or falling depending on which side of rectangular pulse. A digital timing diagram is an example of a well-ordered collection of rectangular pulses. Nyquist pulse A Nyquist pulse is one which meets the Nyquist ISI criterion In communications, the Nyquist ISI criterion describes the conditions which, when satisfied by a comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E (mathematical Constant)
The number is a mathematical constant approximately equal to 2.71828 that is the base of a logarithm, base of the natural logarithm and exponential function. It is sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can invite confusion with Euler numbers, or with Euler's constant, a different constant typically denoted \gamma. Alternatively, can be called Napier's constant after John Napier. The Swiss mathematician Jacob Bernoulli discovered the constant while studying compound interest. The number is of great importance in mathematics, alongside 0, 1, Pi, , and . All five appear in one formulation of Euler's identity e^+1=0 and play important and recurring roles across mathematics. Like the constant , is Irrational number, irrational, meaning that it cannot be represented as a ratio of integers, and moreover it is Transcendental number, transcendental, meaning that it is not a root of any non-zero polynomial with rational coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root Mean Square
In mathematics, the root mean square (abbrev. RMS, or rms) of a set of values is the square root of the set's mean square. Given a set x_i, its RMS is denoted as either x_\mathrm or \mathrm_x. The RMS is also known as the quadratic mean (denoted M_2), a special case of the generalized mean. The RMS of a continuous function is denoted f_\mathrm and can be defined in terms of an integral of the square of the function. In estimation theory, the root-mean-square deviation of an estimator measures how far the estimator strays from the data. Definition The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or the square of the function that defines the continuous waveform. In the case of a set of ''n'' values \, the RMS is : x_\text = \sqrt. The corresponding formula for a continuous function (or waveform) ''f''(''t'') defined over the interval T_1 \le t \le T_2 is : f_\text = \sqrt , and the R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplitude (see below), which are all functions of the magnitude of the differences between the variable's extreme values. In older texts, the phase of a periodic function is sometimes called the amplitude. Definitions Peak amplitude and semi-amplitude For symmetric periodic waves, like sine waves or triangle waves, ''peak amplitude'' and ''semi amplitude'' are the same. Peak amplitude In audio system measurements, telecommunications and others where the measurand is a signal that swings above and below a reference value but is not sinusoidal, peak amplitude is often used. If the reference is zero, this is the maximum absolute value of the signal; if the reference is a mean value ( DC component), the peak amplitude is the maximum ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radar
Radar is a system that uses radio waves to determine the distance ('' ranging''), direction ( azimuth and elevation angles), and radial velocity of objects relative to the site. It is a radiodetermination method used to detect and track aircraft, ships, spacecraft, guided missiles, motor vehicles, map weather formations, and terrain. The term ''RADAR'' was coined in 1940 by the United States Navy as an acronym for "radio detection and ranging". The term ''radar'' has since entered English and other languages as an anacronym, a common noun, losing all capitalization. A radar system consists of a transmitter producing electromagnetic waves in the radio or microwave domain, a transmitting antenna, a receiving antenna (often the same antenna is used for transmitting and receiving) and a receiver and processor to determine properties of the objects. Radio waves (pulsed or continuous) from the transmitter reflect off the objects and return to the receiver, giving ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |